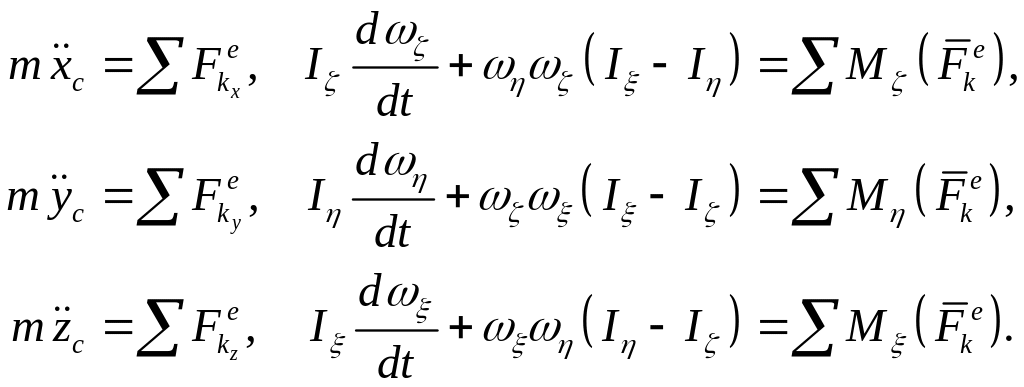- •Теоретическая механика (краткий конспект лекций)
- •Ведение
- •Кинематика основные понятия и задачи кинематики
- •Кинематика точки Способы задания движения точки
- •Векторный способ.
- •Координатный способ.
- •Естественный способ.
- •Скорость точки
- •Скорость точки при векторном задании движения.
- •Скорость точки при координатном задании движения.
- •Скорость точки при естественном задании движения.
- •Определение проекций ускорения на естественные оси при координатном способе задания движения
- •Классификация движений точки по ускорению
- •Простейшие движения твердого тела Поступательное движение тела
- •Вращательное движение тела
- •Сферическое движение твердого тела Определение сферического движения.
- •Теорема Эйлера-Даламбера о конечном повороте
- •Угловая скорость, угловое ускорение
- •Скорость точки тела, участвующего в сферическом движении
- •Мгновенная ось вращения
- •Ускорение точки тела
- •Составное движение точки
- •Дифференцирование вектора в подвижных координатах (Формула Бура)
- •Теорема сложения скоростей
- •Сложение ускорений в составном движении
- •Плоскопараллельное движение твердого тела
- •Разложение движения плоской фигуры на поступательное и вращательное
- •Теорема о скоростях плоской фигуры
- •Мгновенный центр скоростей
- •Примеры определения мцс.
- •Теорема об ускорениях точек плоской фигуры
- •Мгновенный центр ускорений
- •Примеры нахождения мцу.
- •Статика введение в статику Основные понятия статики, область их применения
- •Аксиомы статики Аксиома о равновесии системы двух сил.
- •Аксиома о добавлении (отбрасывании) системы сил эквивалентной нулю.
- •Аксиома параллелограмма сил
- •Аксиома о равенстве сил действия и противодействия.
- •Аксиома затвердевания.
- •Аксиома связей
- •Система сходящихся сил Сложение и разложение сил. Проекция силы на ось и на плоскость.
- •Сходящаяся система сил. Условия равновесия систем сходящихся сил.
- •Теория моментов. Теория пар сил. Момент силы относительно точки на плоскости
- •Векторное представление момента силы
- •Момент силы относительно оси
- •Пара сил. Момент пары
- •Свойства пар сил. Сложение пар сил.
- •Произвольная пространственная система сил Лемма о параллельном переносе силы
- •Основная теорема статики
- •Сравнение понятий главного вектора и равнодействующей.
- •Зависимость между главными моментами, вычисленными относительно различных центров приведения
- •Инварианты системы сил
- •Частные случаи приведения системы сил к центру
- •Условия равновесия произвольной системы сил
- •Различные типы систем сил и условия их равновесия:
- •Теорема о моменте равнодействующей (теорема Вариньона)
- •Применение условий равновесия Различные формы условий равновесия
- •Статически определимые и статически неопределимые задачи
- •Методика решения задач на равновесие пространственной системы сил
- •Распределённые силы
- •Частные случаи распределенных нагрузок.
- •Силы трения Трение скольжения
- •Угол и конус трения
- •Трение качения
- •Центр параллельных сил
- •Центр тяжести объёма, площади, линии
- •Динамика
- •Динамика материальной точки
- •Динамика свободной материальной точки
- •Законы механики Галилея-Ньютона
- •1. Закон инерции
- •2. Основной закон динамики точки
- •3. Закон о равенстве сил действия и противодействия.
- •4. Принцип суперпозиции (закон независимого действия сил)
- •Дифференциальные уравнения движения материальной точки
- •Классификация задач динамики.
- •Первая основная задача динамики
- •Вторая основная задача динамики.
- •Динамика несвободной материальной точки
- •Динамика относительного движения точки
- •Принцип относительности Галилея. Относительный покой.
- •Сила веса и сила тяжести.
- •Основы динамики механических систем Основные понятия и определения Cвязи и их классификация
- •Возможные (виртуальные) перемещения
- •Обобщенные координаты. Число степеней свободы системы
- •Центр масс
- •Моменты инерции твердых тел
- •Количество движения
- •Кинетический момент
- •Кинетическая энергия
- •Элементарный и полный импульс силы
- •Работа силы
- •Силовое поле, силовая функция, потенциальная энергия.
- •Силы инерции. Главный вектор и главный момент сил инерции механической системы
- •Обобщенные силы
- •Введение в динамику механической системы
- •Дифференциальные уравнения движения механической системы
- •Общие теоремы динамики
- •Теорема о движении центра масс
- •Теорема об изменении количества движения
- •Теорема об изменении главного вектора кинетического момента
- •Теорема о кинетическом моменте в относительном движении по отношению к центру масс
- •Теорема об изменении кинетической энергии
- •Закон сохранения механической энергии для точки и системы
- •Принцип Даламбера
- •Принцип Лагранжа (принцип возможных перемещений)
- •Общее уравнение динамики
- •Уравнения Лагранжа II рода
- •Динамика твердого тела
- •Поступательное движение
- •Вращательное движение вокруг неподвижной оси
- •Частные случаи:
- •Нахождение реакций в подшипниках
- •Плоское движение
- •Сферическое движение твердого тела
- •Основы теории колебаний
- •Основные понятия и определения
- •Потенциальная энергия системы
- •Кинетическая энергия системы
- •Диссипативная функция Рэлея
- •Уравнение Лагранжа II рода
- •Свободные колебания системы
- •Ошибка! Закладка не определена.
- •Затухающие колебания системы
- •Ошибка! Закладка не определена.
- •Ошибка! Закладка не определена.
- •Вынужденные колебания системы
- •Ошибка! Закладка не определена.Ошибка! Закладка не определена.
- •Ошибка! Закладка не определена.
- •Исследование вынужденных колебаний
- •Резонанс
- •Ошибка! Закладка не определена.
- •Биения.
- •Ошибка! Закладка не определена.
- •Ошибка! Закладка не определена.
- •Критерии и условия, используемые при исследовании колебательных движений механических систем
- •Коэффициент динамичности.
- •Ошибка! Закладка не определена.
- •Ошибка! Закладка не определена.
- •Коэффициент передачи силы
- •Список литературы Основной
- •Дополнительный
Плоское движение
Из кинематики известно, что плоское движение твёрдого тела можно разложить на два простейших: поступательное вместе с полюсом и вращательное вокруг полюса. Примем за полюс центр масс тела. Тогда кинематические уравнения плоского движения запишутся в виде:
![]()
Для изучения плоского движения твёрдого
тела достаточно составить три
дифференциальных уравнения, связывающие
величины
![]() с действующими на тело внешними силами.
с действующими на тело внешними силами.
Поступательная часть движения определяется дифференциальным уравнением поступательного движения (теоремой о движении центра масс)
![]()
Третье уравнение плоского движения получим, применив теорему об изменении кинетического момента относительно подвижной оси, проходящей через центр масс
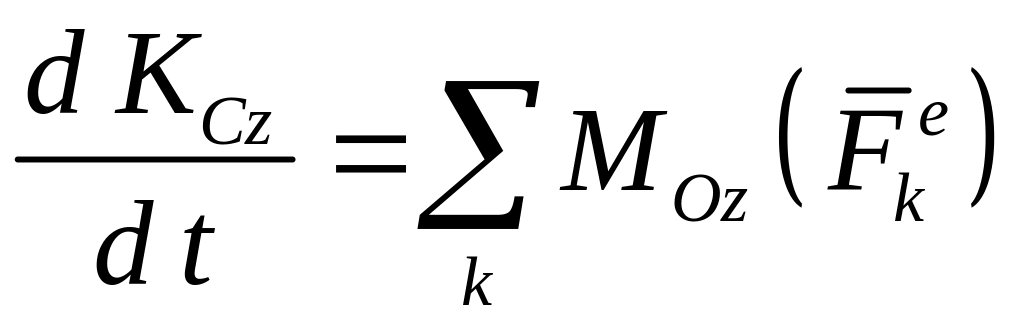 .
.
Так как кинетический момент твёрдого
тела относительно оси
![]() можно определить по формуле
можно определить по формуле
![]() то, подставляя его в теорему, получим
то, подставляя его в теорему, получим
 .
.
Таким образом, дифференциальные уравнения плоского движения твёрдого тела имеют вид
![]() .
.
Сферическое движение твердого тела
Твердое тело с одной неподвижной точкой
имеет три степени свободы. Классическими
параметрами, определяющими положение
этого тела в пространстве, являются
три угла Эйлера:![]() .
Если
известны как функции времени, то известно
и движение твердого тела с одной
неподвижной точкой (сферическое
движение) (рис. 3.6).
.
Если
известны как функции времени, то известно
и движение твердого тела с одной
неподвижной точкой (сферическое
движение) (рис. 3.6).
Для составления дифференциальных уравнений сферического движения запишем теорему об изменении кинетического момента в дифференциальной форме
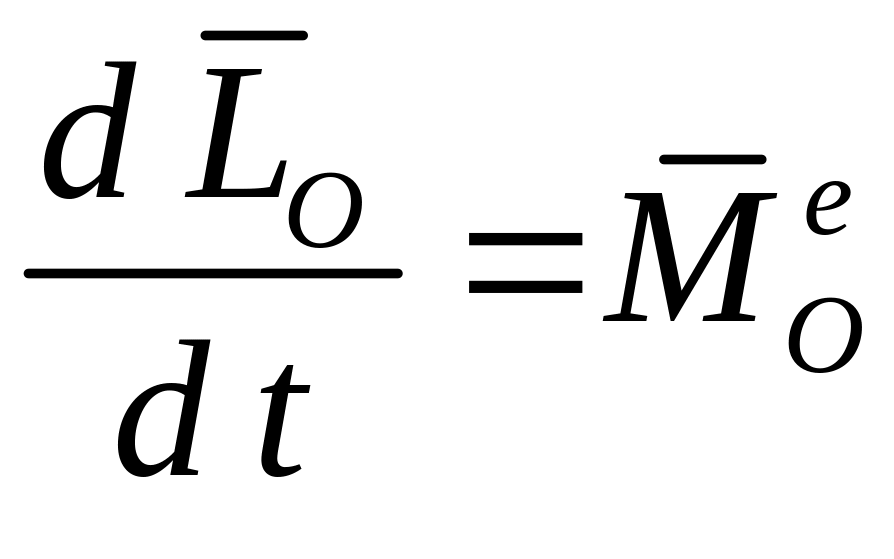 ,
,
где
![]() — кинетический момент твердого тела,
совершающего сферическое движение
относительно неподвижной точки
;
— кинетический момент твердого тела,
совершающего сферическое движение
относительно неподвижной точки
;
![]() —
главный момент внешних сил относительно
неподвижного центра
.
—
главный момент внешних сил относительно
неподвижного центра
.
Чтобы записать
соответствующие формулы в наиболее
простом виде возьмем в качестве
координатных – подвижные главные оси
инерции
![]() жестко связанные
с телом. Тогда проекции кинетического
момента на оси координат можно записать
в виде
жестко связанные
с телом. Тогда проекции кинетического
момента на оси координат можно записать
в виде
![]()
Уравнения движения (динамические уравнения Эйлера) в этом случае примут вид:
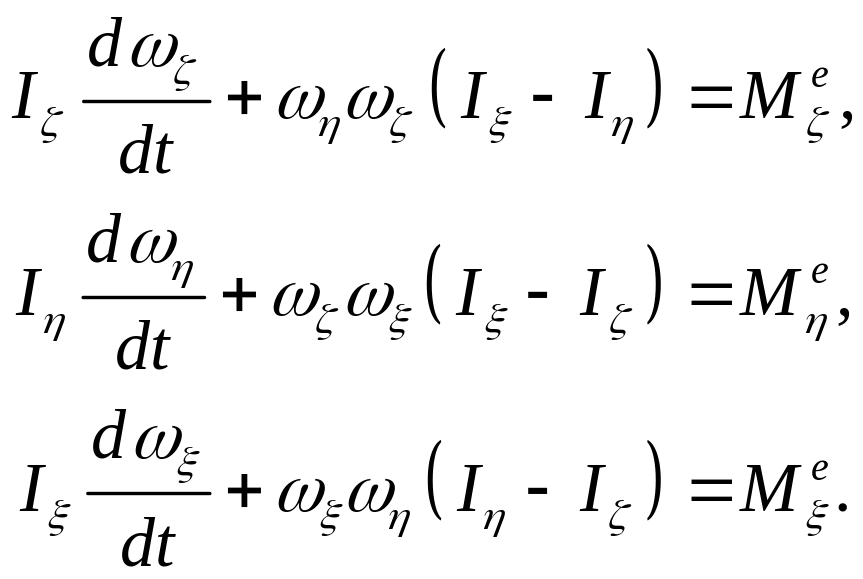
где
![]() – моменты инерции тела относительно
его осей инерции в точке О;
– моменты инерции тела относительно
его осей инерции в точке О;
![]() –
главные моменты внешних сил, приложенных
к телу, относительно этих же осей.
–
главные моменты внешних сил, приложенных
к телу, относительно этих же осей.
К динамическим уравнениям Эйлера следует присоединить кинематические уравнения Эйлера:
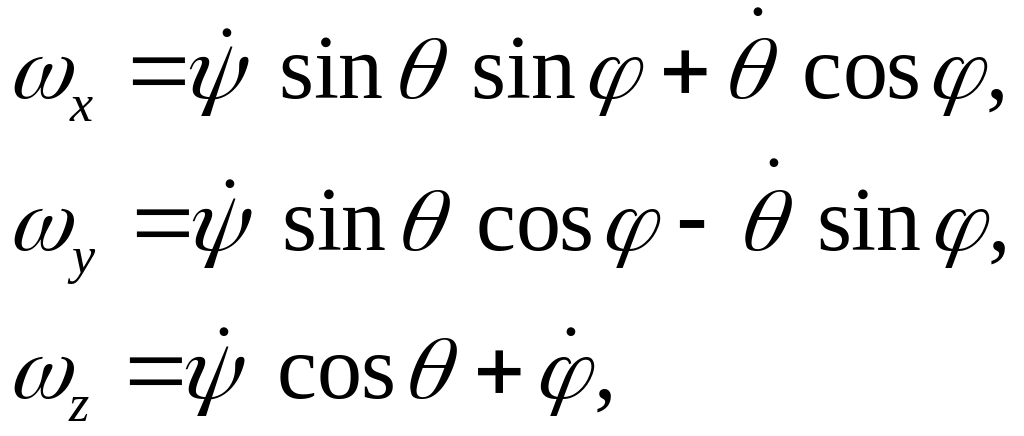
которые выражают проекции вектора угловой скорости вращения твердого тела на оси подвижной системы координат, скрепленные с телом через углы Эйлера и их производные по времени.

Рис. 3. 6 Сферическое движение твердого тела.
Динамические и кинематические уравнения Эйлера образуют систему шести нелинейных дифференциальных уравнений первого порядка; интегрирование этой системы представляет сложную математическую задачу. Для интегрирования этих уравнений при решении конкретных задач обычно используют те или иные приближенные математические методы.
Условия интегрируемости уравнений движения
Для твердого тела, вращающегося вокруг неподвижной точки, в трех случаях существует система дифференциальных уравнений, из которых углы Эйлера определяются в квадратурах, т. е. путем вычисления интегралов. Эти частные случаи называют условиями интегрируемости.
Случай Эйлера
Тело имеет произвольную форму, но
закреплено в его центре масс, т. е.
![]() .
Углы Эйлера выражаются в этом случае
через специальные эллиптические
функции.
.
Углы Эйлера выражаются в этом случае
через специальные эллиптические
функции.
Случай Лагранжа
Тело имеет ось симметрии, например
.
В силу симметрии
![]() и эллипсоид инерции для закрепленной
точки будет эллипсоидом вращения.
Закрепленная точка
и центр масс
и эллипсоид инерции для закрепленной
точки будет эллипсоидом вращения.
Закрепленная точка
и центр масс
![]() расположены на оси симметрии. В этом
случае могут быть указаны шесть
независимых первых интегралов, из
которых углы Эйлера вычисляются в
квадратурах.
расположены на оси симметрии. В этом
случае могут быть указаны шесть
независимых первых интегралов, из
которых углы Эйлера вычисляются в
квадратурах.
Случай Ковалевской
В этом случае![]() .
Закрепленная точка располагается на
оси симметрии
,
а центр масс находится в экваториальной
плоскости эллипсоида инерции для
неподвижной точки тела.
.
Закрепленная точка располагается на
оси симметрии
,
а центр масс находится в экваториальной
плоскости эллипсоида инерции для
неподвижной точки тела.
Свободное движение твердого тела
Свободное твердое тело имеет шесть степеней свободы. Движение этого тела можно разложить на переносное поступательное вместе с полюсом, в качестве которого обычно выбирают центр масс , и относительное движение вокруг центра масс (рис. 3.7).

Рис. 3. 7 Свободное движение твердого тела.
Для составления дифференциальных уравнений свободного движения применим теорему о движения центра масс
![]()
и теорему об изменении кинетического момента в относительном движении по отношению к центру масс
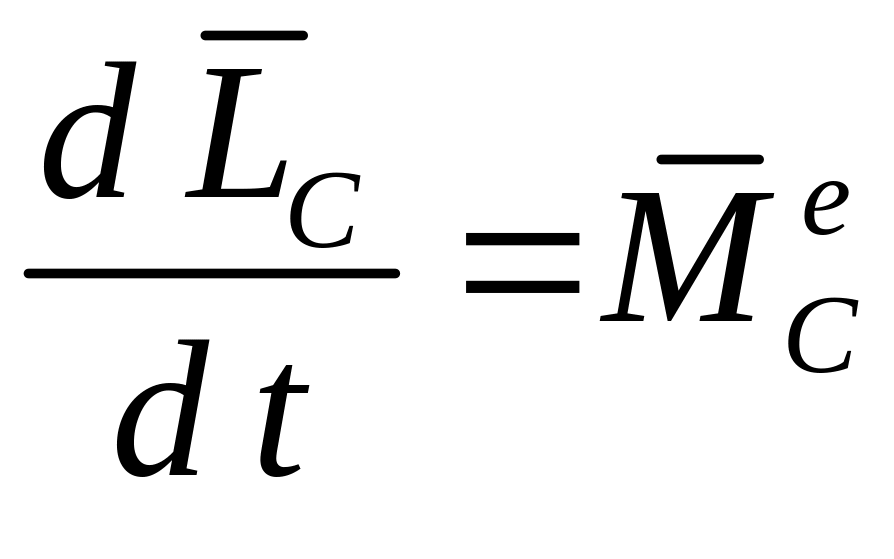 .
.
Совмещая оси подвижной системы координат
с главными осями инерции
![]() и записывая данные теоремы в проекциях
на оси подвижной и неподвижной системы,
получим шесть дифференциальных уравнений
движения свободного твердого тела:
и записывая данные теоремы в проекциях
на оси подвижной и неподвижной системы,
получим шесть дифференциальных уравнений
движения свободного твердого тела: