Теорема об изменении главного вектора кинетического момента

Первая производная по времени от кинетического момента системы, вычисленного относительно центра , равна геометрической сумме моментов всех внешних сил, действующих на систему, взятых относительно того же центра

.

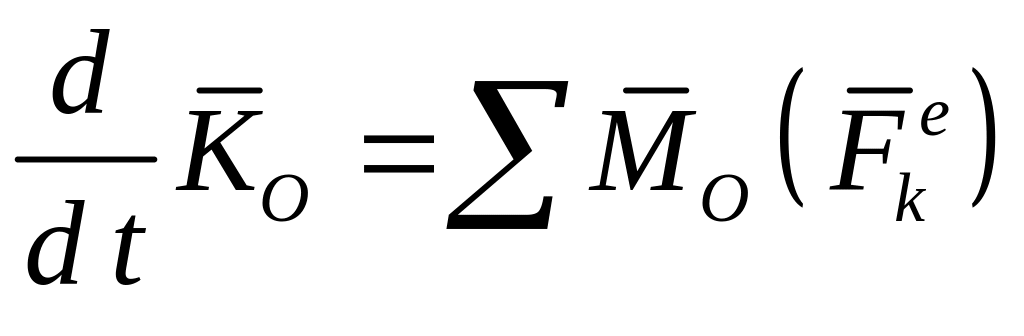Теорема о кинетическом моменте в относительном движении по отношению к центру масс

Теорема об изменении кинетического момента относительно центра масс в относительном движении сохраняет тот же вид, что и относительно неподвижного центра в абсолютном движении

.

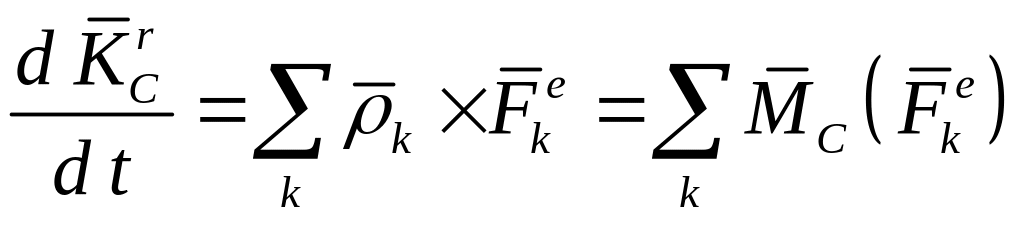Теорема об изменении кинетической энергии

Дифференциал от кинетической энергии системы равен сумме элементарных работ всех внутренних и внешних сил, действующих на систему

.

Проинтегрировав это соотношение, получим конечную формулировку данной теоремы

.

Её можно записать и в форме мощностей внешних и внутренних сил

.

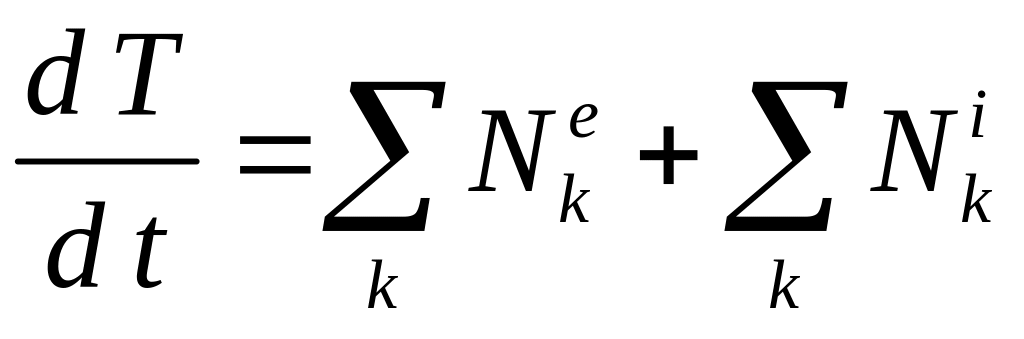Отличительной особенностью теоремы об изменении кинетической энергии системы состоит в том, что только в одной этой теореме из всех общих теорем динамики системы внутренние силы явным образом фигурируют в формулировке теоремы.

Закон сохранения механической энергии для точки и системы

Величина, равная сумме кинетической и потенциальной энергий (механической энергии), не меняется в процессе движения механической системы в потенциальном поле

.

Это соотношение является одним из первых интегралов движения — интеграл энергии. Из него следует, что увеличению кинетической энергии соответствует уменьшение потенциальной энергии и наоборот.

Механические системы, в которых выполняется этот закон, называются консервативными.

Принцип Даламбера

Если в произвольный момент времени к каждой из точек, входящих в систему, приложить кроме фактически действующих на неё внутренних и внешних сил силы инерции, то система будет находиться в состоянии покоя.

Главный вектор внешних сил уравновешивается главным вектором сил инерции

.

Главный момент внешних сил и главный момент сил инерции, вычисленные относительно произвольного центра , взаимно уравновешиваются

.

Принцип Лагранжа (принцип возможных перемещений)

Для равновесия механической системы с удерживающими идеальными стационарными связями необходимо и достаточно, чтобы сумма элементарных работ всех активных сил на любом возможном перемещении системы равнялась нулю

.

Простота выражения элементарной работы через обобщённые силы и независимость вариаций обобщённых координат друг от друга позволяет записать принцип Лагранжа в виде

, где .

Т.е. для равновесия механической системы с идеальными, удерживающими связями необходимо и достаточно, чтобы все обобщённые силы равнялись нулю.

Для консервативной механической системы условия равновесия примут вид

, где .

Общее уравнение динамики

Общее уравнение динамики системы получается при последовательном применении к ней вначале принципа Даламбера, а затем принципа Лагранжа

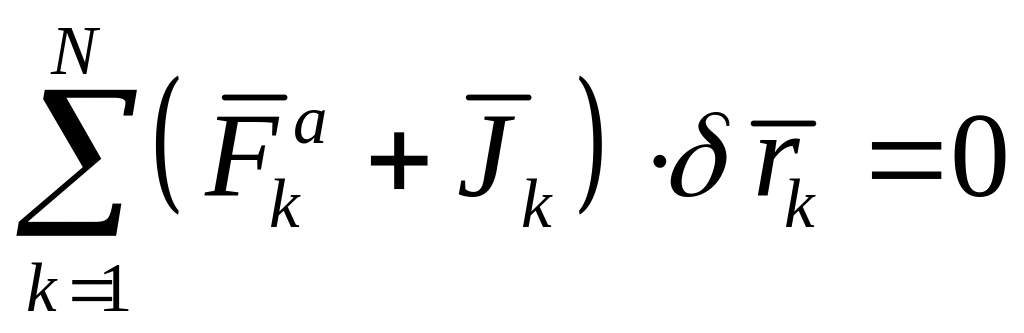или .

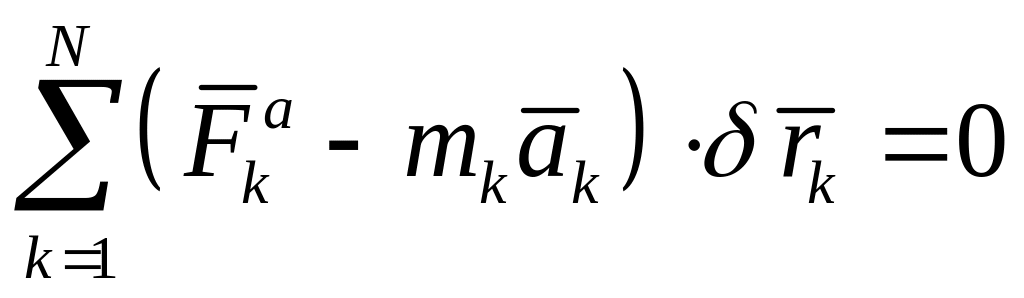При любых движениях системы с идеальными связями в каждый момент времени выполняется условие равенства нулю суммы элементарных работ всех активных сил и сил инерции на любом возможном перемещении.

Уравнения Лагранжа II рода

Уравнения Лагранжа II рода имеют вид

.

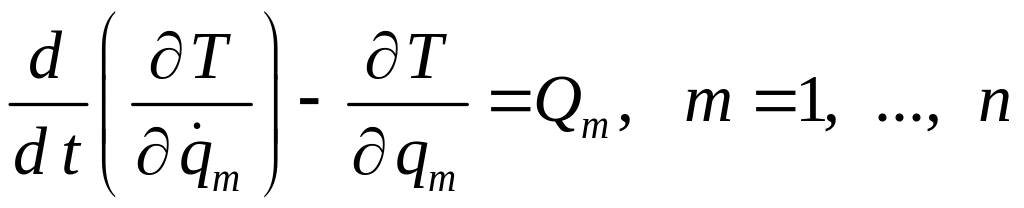Число уравнений Лагранжа II рода равно числу степеней свободы голономной системы. Сами уравнения с точки зрения математика представляют собой обыкновенные дифференциальные уравнения второго порядка относительно неизвестных обобщённых координат, рассматриваемых как функции времени.

Для консервативных голономных систем уравнения Лагранжа имеют вид

,

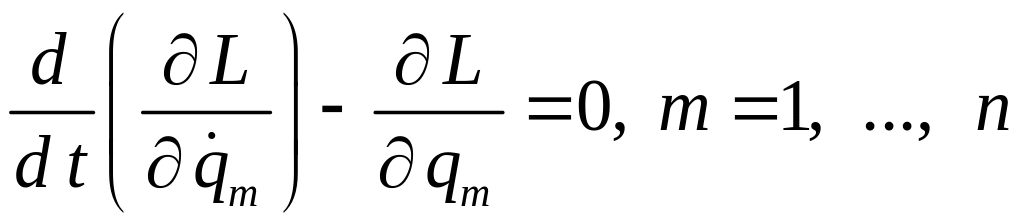где — функция Лагранжа.