3. Закон о равенстве сил действия и противодействия.

Третий закон Ньютона утверждает, что при взаимодействии двух тел между ними возникают силы, равные по величине и противоположные по направлению

.

Таким образом, в природе не существует одностороннего действия. Сила действия и сила противодействия приложены к различным телам и поэтому не могут компенсировать друг друга (не являются системой сил эквивалентной нулю).

4. Принцип суперпозиции (закон независимого действия сил)

При одновременном действии на материальную точку нескольких сил ускорение точки относительно инерциальной системы отсчета соответствует действию одной силы, величина которой равна сумме сил действующих на точку

Закон независимого действия сил следует понимать как закон суперпозиции сил, т.е. как закон сложения ускорений от действия отдельных сил. С учетом этого закона основное уравнение динамики материальной точки принимает вид

.

Дифференциальные уравнения движения материальной точки

Пусть материальная точка движется под действием приложенных к ней сил. Подставив во второй закон Ньютона ускорение в виде второй производной по времени от радиус-вектора, получим дифференциальное уравнение движения материальной точки

.

Проектируя это векторное уравнение на координатные оси декартовой системы координат, получим дифференциальные уравнения движения точки

.

В случае прямолинейного движения точки имеем только одно уравнение

.

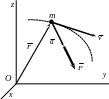
Уравнения движения в проекциях на оси естественных координат имеют вид

.

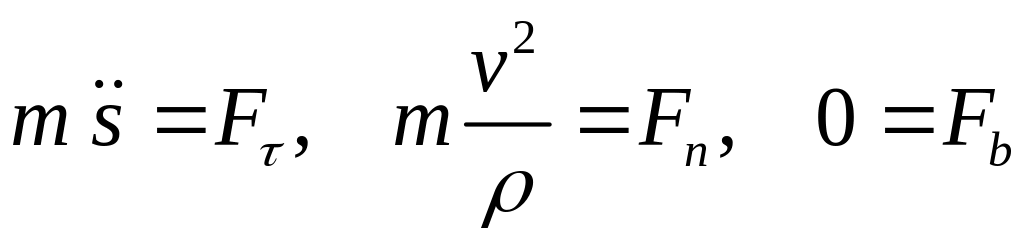Основное уравнение динамики точки остается справедливым и для несвободной материальной точки, на которую наложены связи. В этом случае, в число действующих на точку сил, следует включить и силы реакций связей.

Классификация задач динамики.

В динамике решают две основные задачи:

Первая основная задача динамики

По известным кинематическим уравнениям и массе точки требуется определить силу, вызывающую заданное движение.

Задача решается двойным дифференцированием радиус-вектора материальной точки по времени, с последующим умножением результата на массу.

Вторая основная задача динамики.

По заданным силам и массе точки требуется определить закон движения.

Вторая основная задача связана с интегрированием. В соответствии с этим можно говорить и об относительной сложности этих задач. Обычно вторая основная задача значительно сложнее первой.

Второй закон Ньютона можно записать в виде системы дифференциальных уравнений второго порядка:

,

или в проекциях на оси декартовой системы координат

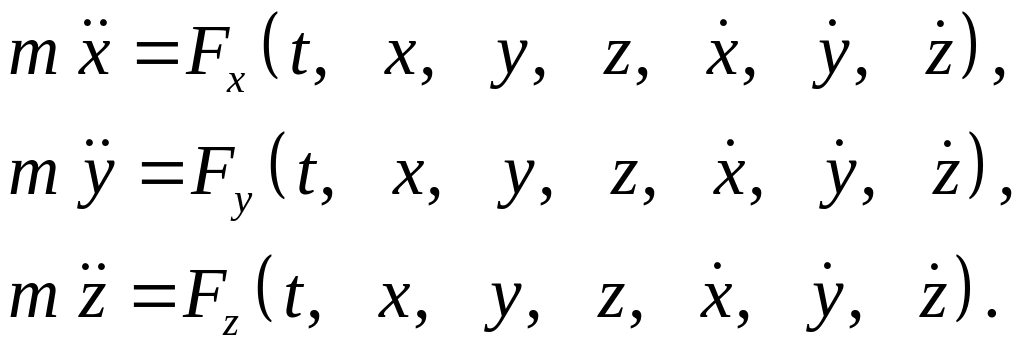
Для нахождения уравнений движения точки нужно дважды проинтегрировать эти уравнения. Как известно, при интегрировании дифференциального уравнения второго порядка, решение содержит две константы интегрирования, т.е. для случая трех уравнений имеется шесть произвольных постоянных. Подставляя найденные значения констант интегрирования в общее решение дифференциальных уравнений движения, получим частные решения, справедливые для данных в задаче начальных условий:

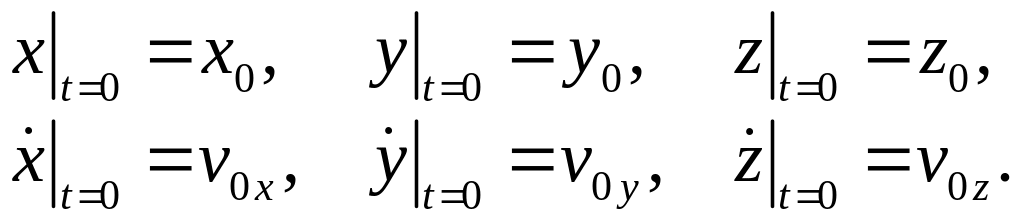
С учетом принятых обозначений эти решения примут вид

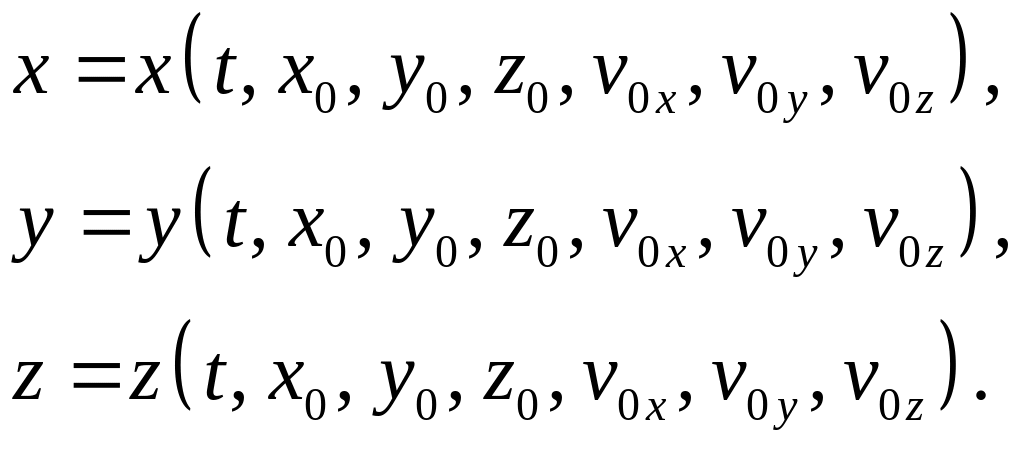
Заметим, что под действием одной системы сил точка может совершать целый класс движений, определяемых начальными условиями.

Если каким-либо образом удалось сразу получить первые интегралы, то дальнейшее решение задачи сводится к однократному интегрированию трёх дифференциальных уравнений первого порядка.