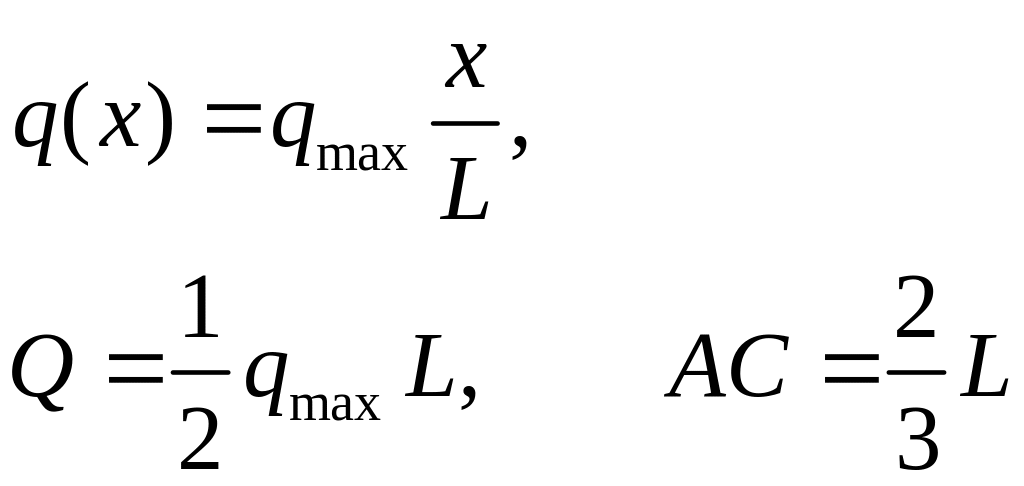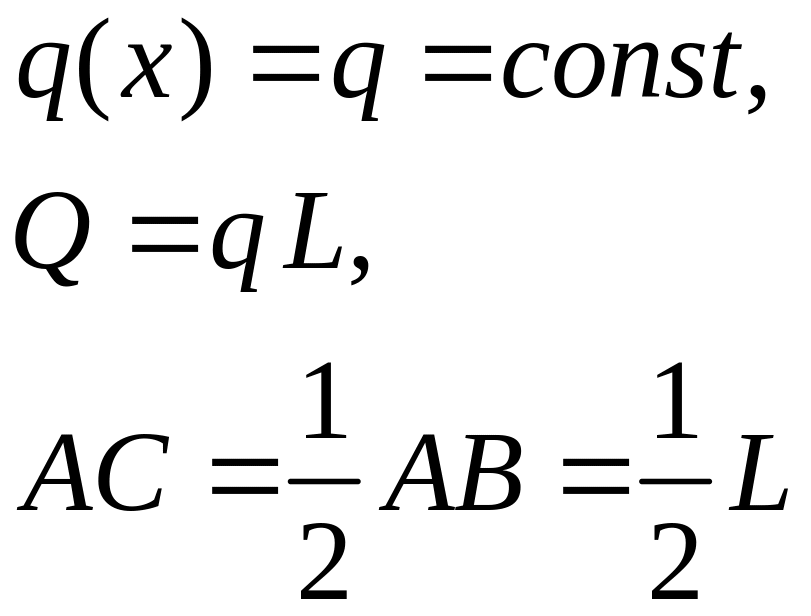- •Теоретическая механика (краткий конспект лекций)
- •Ведение
- •Кинематика основные понятия и задачи кинематики
- •Кинематика точки Способы задания движения точки
- •Векторный способ.
- •Координатный способ.
- •Естественный способ.
- •Скорость точки
- •Скорость точки при векторном задании движения.
- •Скорость точки при координатном задании движения.
- •Скорость точки при естественном задании движения.
- •Определение проекций ускорения на естественные оси при координатном способе задания движения
- •Классификация движений точки по ускорению
- •Простейшие движения твердого тела Поступательное движение тела
- •Вращательное движение тела
- •Сферическое движение твердого тела Определение сферического движения.
- •Теорема Эйлера-Даламбера о конечном повороте
- •Угловая скорость, угловое ускорение
- •Скорость точки тела, участвующего в сферическом движении
- •Мгновенная ось вращения
- •Ускорение точки тела
- •Составное движение точки
- •Дифференцирование вектора в подвижных координатах (Формула Бура)
- •Теорема сложения скоростей
- •Сложение ускорений в составном движении
- •Плоскопараллельное движение твердого тела
- •Разложение движения плоской фигуры на поступательное и вращательное
- •Теорема о скоростях плоской фигуры
- •Мгновенный центр скоростей
- •Примеры определения мцс.
- •Теорема об ускорениях точек плоской фигуры
- •Мгновенный центр ускорений
- •Примеры нахождения мцу.
- •Статика введение в статику Основные понятия статики, область их применения
- •Аксиомы статики Аксиома о равновесии системы двух сил.
- •Аксиома о добавлении (отбрасывании) системы сил эквивалентной нулю.
- •Аксиома параллелограмма сил
- •Аксиома о равенстве сил действия и противодействия.
- •Аксиома затвердевания.
- •Аксиома связей
- •Система сходящихся сил Сложение и разложение сил. Проекция силы на ось и на плоскость.
- •Сходящаяся система сил. Условия равновесия систем сходящихся сил.
- •Теория моментов. Теория пар сил. Момент силы относительно точки на плоскости
- •Векторное представление момента силы
- •Момент силы относительно оси
- •Пара сил. Момент пары
- •Свойства пар сил. Сложение пар сил.
- •Произвольная пространственная система сил Лемма о параллельном переносе силы
- •Основная теорема статики
- •Сравнение понятий главного вектора и равнодействующей.
- •Зависимость между главными моментами, вычисленными относительно различных центров приведения
- •Инварианты системы сил
- •Частные случаи приведения системы сил к центру
- •Условия равновесия произвольной системы сил
- •Различные типы систем сил и условия их равновесия:
- •Теорема о моменте равнодействующей (теорема Вариньона)
- •Применение условий равновесия Различные формы условий равновесия
- •Статически определимые и статически неопределимые задачи
- •Методика решения задач на равновесие пространственной системы сил
- •Распределённые силы
- •Частные случаи распределенных нагрузок.
- •Силы трения Трение скольжения
- •Угол и конус трения
- •Трение качения
- •Центр параллельных сил
- •Центр тяжести объёма, площади, линии
- •Динамика
- •Динамика материальной точки
- •Динамика свободной материальной точки
- •Законы механики Галилея-Ньютона
- •1. Закон инерции
- •2. Основной закон динамики точки
- •3. Закон о равенстве сил действия и противодействия.
- •4. Принцип суперпозиции (закон независимого действия сил)
- •Дифференциальные уравнения движения материальной точки
- •Классификация задач динамики.
- •Первая основная задача динамики
- •Вторая основная задача динамики.
- •Динамика несвободной материальной точки
- •Динамика относительного движения точки
- •Принцип относительности Галилея. Относительный покой.
- •Сила веса и сила тяжести.
- •Основы динамики механических систем Основные понятия и определения Cвязи и их классификация
- •Возможные (виртуальные) перемещения
- •Обобщенные координаты. Число степеней свободы системы
- •Центр масс
- •Моменты инерции твердых тел
- •Количество движения
- •Кинетический момент
- •Кинетическая энергия
- •Элементарный и полный импульс силы
- •Работа силы
- •Силовое поле, силовая функция, потенциальная энергия.
- •Силы инерции. Главный вектор и главный момент сил инерции механической системы
- •Обобщенные силы
- •Введение в динамику механической системы
- •Дифференциальные уравнения движения механической системы
- •Общие теоремы динамики
- •Теорема о движении центра масс
- •Теорема об изменении количества движения
- •Теорема об изменении главного вектора кинетического момента
- •Теорема о кинетическом моменте в относительном движении по отношению к центру масс
- •Теорема об изменении кинетической энергии
- •Закон сохранения механической энергии для точки и системы
- •Принцип Даламбера
- •Принцип Лагранжа (принцип возможных перемещений)
- •Общее уравнение динамики
- •Уравнения Лагранжа II рода
- •Динамика твердого тела
- •Поступательное движение
- •Вращательное движение вокруг неподвижной оси
- •Частные случаи:
- •Нахождение реакций в подшипниках
- •Плоское движение
- •Сферическое движение твердого тела
- •Основы теории колебаний
- •Основные понятия и определения
- •Потенциальная энергия системы
- •Кинетическая энергия системы
- •Диссипативная функция Рэлея
- •Уравнение Лагранжа II рода
- •Свободные колебания системы
- •Ошибка! Закладка не определена.
- •Затухающие колебания системы
- •Ошибка! Закладка не определена.
- •Ошибка! Закладка не определена.
- •Вынужденные колебания системы
- •Ошибка! Закладка не определена.Ошибка! Закладка не определена.
- •Ошибка! Закладка не определена.
- •Исследование вынужденных колебаний
- •Резонанс
- •Ошибка! Закладка не определена.
- •Биения.
- •Ошибка! Закладка не определена.
- •Ошибка! Закладка не определена.
- •Критерии и условия, используемые при исследовании колебательных движений механических систем
- •Коэффициент динамичности.
- •Ошибка! Закладка не определена.
- •Ошибка! Закладка не определена.
- •Коэффициент передачи силы
- •Список литературы Основной
- •Дополнительный
Методика решения задач на равновесие пространственной системы сил
Любая задача статики изучаемого курса может быть решена по следующему плану:
выделить тело (элемент) или систему тел, равновесие которых будем рассматривать (использование аксиомы освобождения от связей);
расставить силы, действующие на выделенные элементы. Т. к. кроме активных сил на выделенные элементы действуют реакции отброшенных связей, то этот пункт существенно зависит от первого и, обычно, выполняется вместе с ним;
дать анализ полученной системы сил, выяснить, является ли задача статически определённой;
записать условия равновесия и произвести над ними действия с целью определения неизвестных;
дать анализ полученного ответа.
Распределённые силы
До сих пор рассматривались силы, приложенные в одной точке, которые называются сосредоточенными. В действительности взаимодействие одного тела с другим осуществляется либо по некоторой площадке, либо по объёму тела. Пример поверхностных сил — давление воды на стенку плотины, объёмных — силы тяжести — они распределены по всему объёму тела, но часто, для удобства, мы заменяем эти силы их равнодействующей, приложенной к центру тяжести.
Распределённые силы характеризуются интенсивностью и направлением действия. Интенсивностью распределённой силы называется величина силы, приходящаяся на единицу объёма, площади или длины линии.
Силы принимаются распределёнными по линии в том случае, когда размерами тела в поперечном направлении можно пренебречь по сравнению с его длиной. Такие тела называются стержнями или балками. Распределёнными, обычно, бывают параллельные или сходящиеся силы, однако, распределёнными могут быть и пары сил.
Рассмотрим вопросы
замены распределённых сил сосредоточенными
силами. Пусть силы распределены по
отрезку АВ, длиной L.
Разобьём весь отрезок AB на элементарные
участки![]() .
На каждый из них
действует сила равная
.
На каждый из них
действует сила равная![]() ,
т. к. из-за малости участка интенсивность
в его пределах можно считать постоянной.
Суммируя элементарные
силы, найдём равнодействующую. Величина
её равна главному вектору
,
т. к. из-за малости участка интенсивность
в его пределах можно считать постоянной.
Суммируя элементарные
силы, найдём равнодействующую. Величина
её равна главному вектору
![]()
При устремлении к нулю элементарной длины сумма сил перейдёт в интеграл
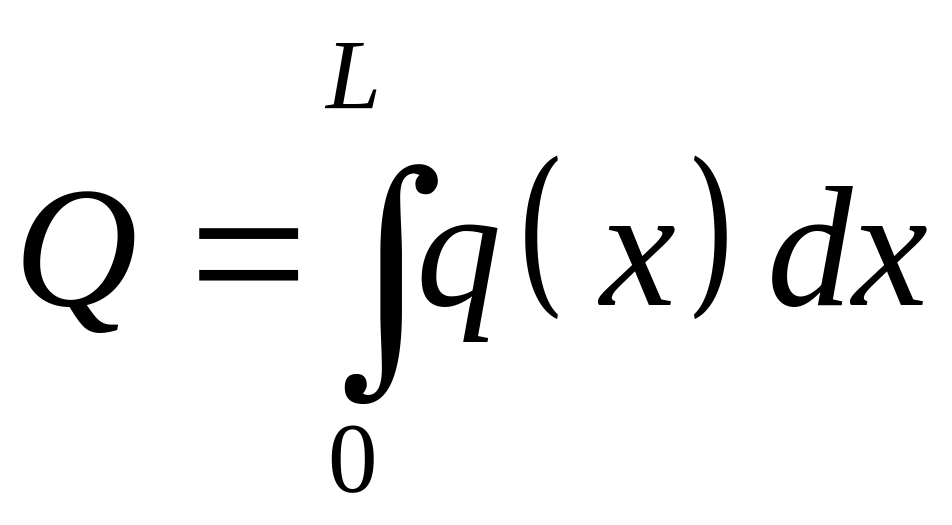 .
.
Т очка
приложения равнодействующей силы
определяется с помощью теоремы Вариньона:
очка
приложения равнодействующей силы
определяется с помощью теоремы Вариньона:
![]() ,
,
или при предельном переходе
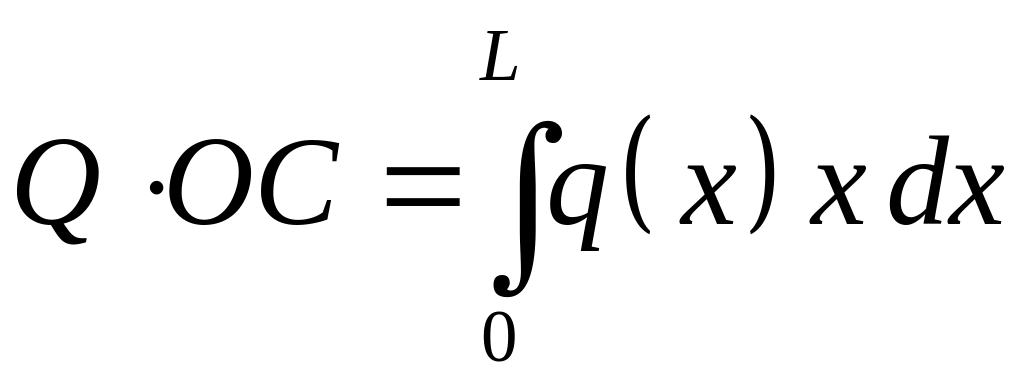
Откуда окончательно
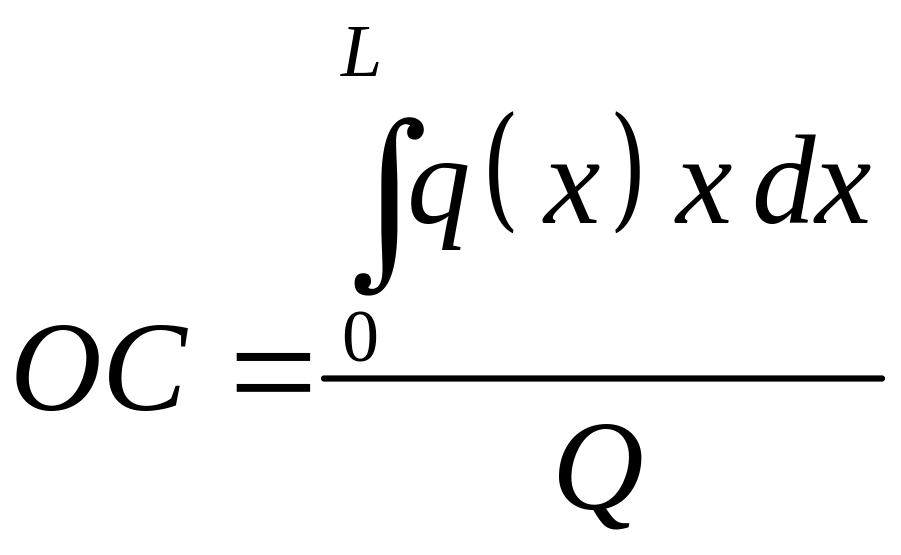
Частные случаи распределенных нагрузок.
Распределение с постоянной интенсивностью.
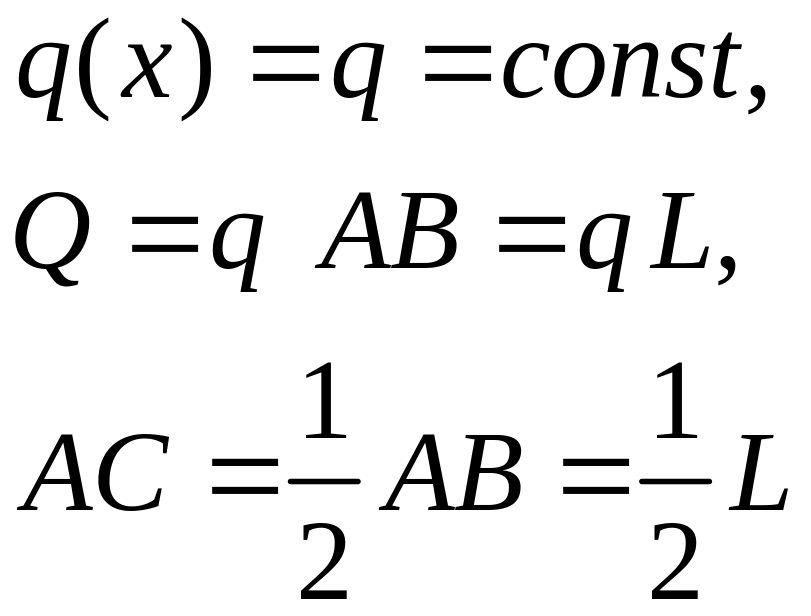
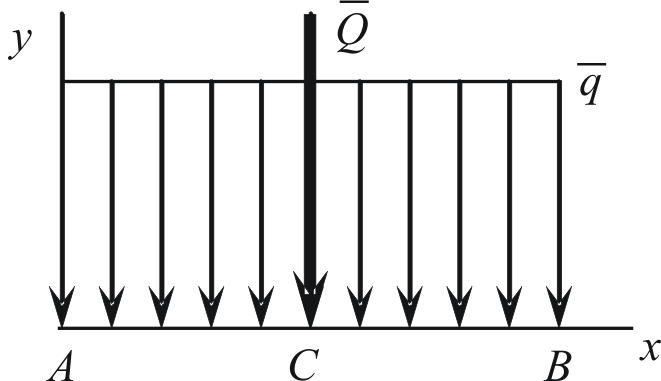
Распределение с линейно изменяющейся интенсивностью.
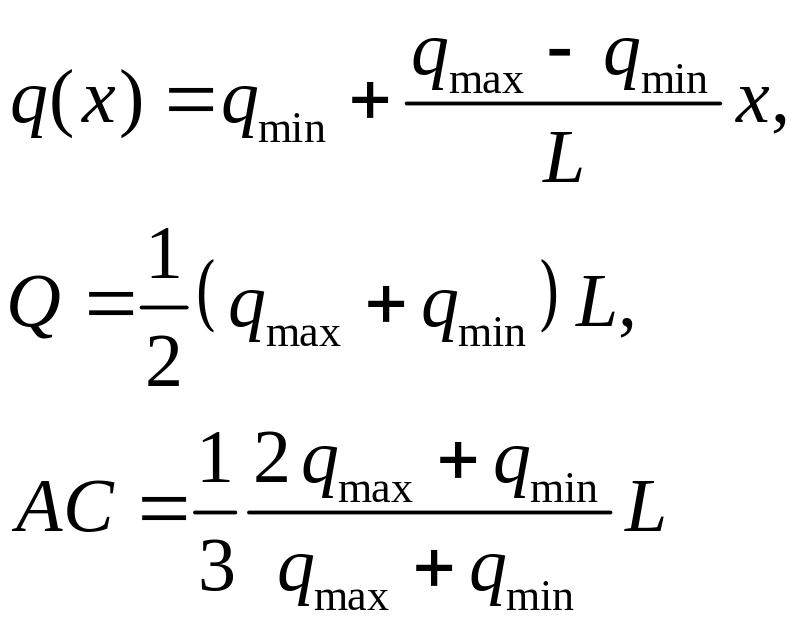
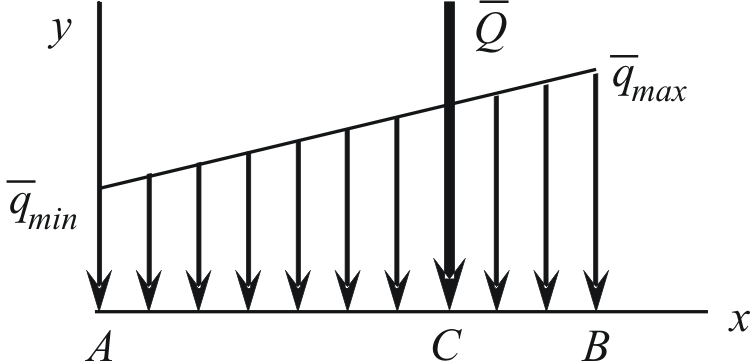
Если
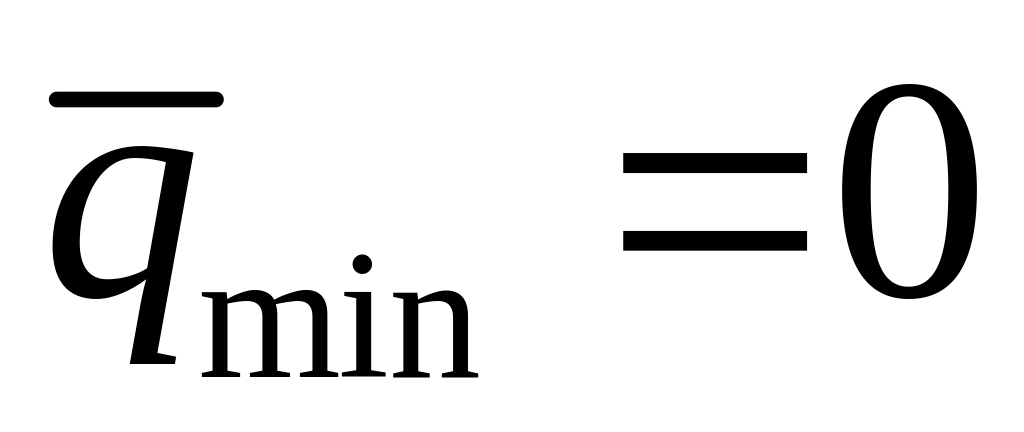 ,
то получаем треугольное распределение
,
то получаем треугольное распределение
|
|
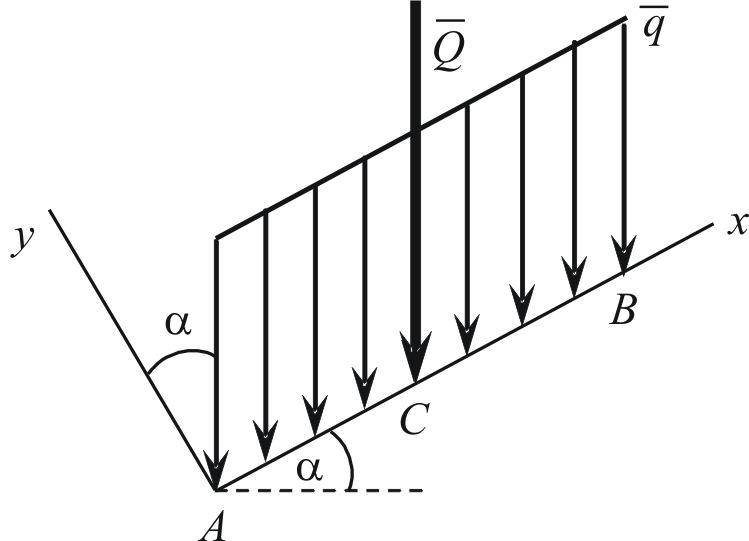
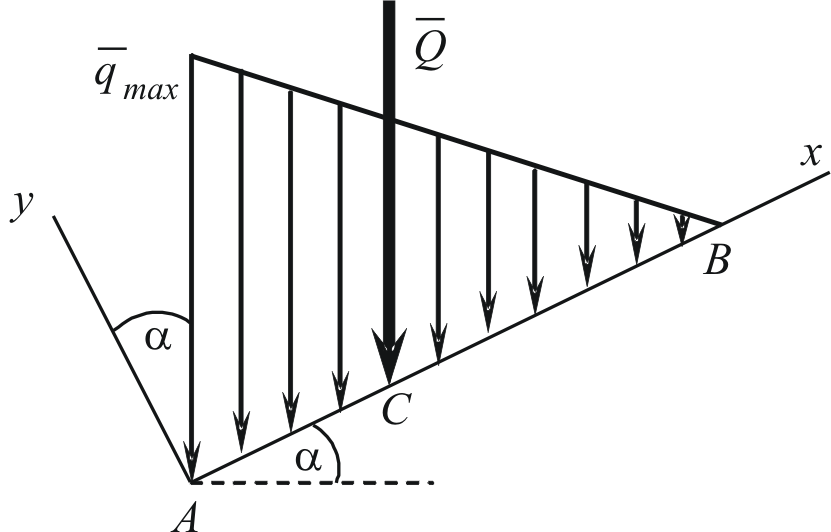
Распределённая нагрузка, заданная под углом
Распределение с постоянной интенсивностью
|
|
Распределение с линейно изменяющейся интенсивностью.
|
|
В последних случаях равнодействующая не равна площади фигуры, образованной линией распределения интенсивности, и не зависит от угла наклона интенсивности к опорной линии.