Аксиомы статики Аксиома о равновесии системы двух сил.

Свободное, абсолютно твердое тело находится в равновесии под действием двух сил только в том случае, когда эти силы равны по величине и направлены вдоль одной линии действия в противоположные стороны.

Рис. 2. 2. Аксиома о равновесии двух сил

Аксиома о добавлении (отбрасывании) системы сил эквивалентной нулю.

Если к системе сил добавить (отбросить) другую систему, эквивалентную нулю, то полученная система будет эквивалентна первой (рис.2.3 а).

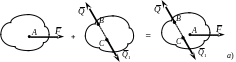
Рис. 2. 3. Аксиома одобавлении (отбрасывании) системы сил эквиваленной нулю

Основываясь на этой аксиоме, можно переносить силу вдоль линии ее действия в пределах абсолютно твердого тела. В этом случае векторы, обозначающие силы, теряют свое наименование “приложенных” к определенной точке и становятся "скользящими" (рис. 2.3 б)

Аксиома параллелограмма сил

Совокупность сил, приложенных к одной точке, может быть заменена одной силой в соответствии с правилом параллелограмма или треугольника. И наоборот, одна сила может быть разложена на совокупность нескольких сил, приложенных в той же точке.

Рис. 2. 4. Сложение двух сил

Опытные данные, лежащие в основе этой аксиомы, дают основание считать силу векторной величиной. Вектор характеризуется величиной, направлением, точкой приложения, и складывается с другими векторами по закону параллелограмма.

Аксиома о равенстве сил действия и противодействия.

Следующей аксиомой является то, что обычно называют третьим законом Ньютона: два тела взаимодействуют между собой с силами, равными по величине, противоположными по направлению и приложенными к различным взаимодействующим телам. На основе этой аксиомы строится метод решения задач, называемый методом сечений.

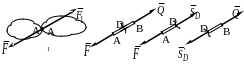
Рис. 2. 5. Аксиома о равенстве сил действия и противодействия

Аксиома затвердевания.

Существенные сведения о равновесии деформируемых тел можно получить, воспользовавшись принципом отвердевания: если деформируемое тело находится в равновесии, то замена его или отдельных его частей соответствующими абсолютно твердыми телами не изменяет первоначального состояния равновесия. То есть условия равновесия абсолютно твердого тела являются необходимыми, но не достаточными для равновесия деформируемого тела.

Аксиома связей

Тела, равновесие которых изучается, в большинстве случаев контактируют с другими окружающими телами, ограничивающими свободу данного тела. Тела, ограничивающие свободу данного тела, являются по отношению к нему связями. Воздействия связей на тело называются реакциями связей. Мысленно отбросив все связи и заменив их воздействие реакциями, получим свободное тело, на которое действуют как приложенные (активные) так и реактивные силы (реакции связей). Этот прием имеет название принципа освобождаемости от связей.

Ниже на рис.2.6 – 2.10 представлены примеры связей и их реакций

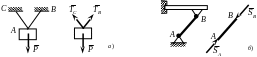
Рис.2.6. Натянутые гибкие нити (а) и стержни (б)

Рис. 2.7 Идеально гладкая (а) и шероховатая (б) поверхности (контакт по поверхности)

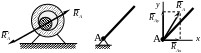
Рис. 2.8 Неподвижная цилиндрическая шарнирная опора

Рис. 2.9 Подвижная цилиндрическая шарнирная опора (опора на каток)

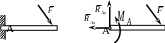
Рис. 2.10 Жесткая заделка