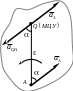
Мгновенный центр ускорений

В любой момент времени в плоскости движущейся фигуры существует одна единственная точка, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений (МЦУ).

Доказательство следует из способа определения положения этой точки. Примем за полюс точку А, предполагая известным её ускорение. Раскладываем движение плоской фигуры на поступательное и вращательное. Пользуясь теоремой сложения ускорений, записываем ускорение искомой точки и приравниваем его нулю.

Отсюда следует, что , т. е. относительное ускорение точки Q равно ускорению полюса А по величине и направлено в противоположную сторону. Это возможно только в том случае, если углы наклона относительного ускорения и ускорения полюса А к прямой, соединяющей точку Q, с полюсом А одинаковы.

, , .

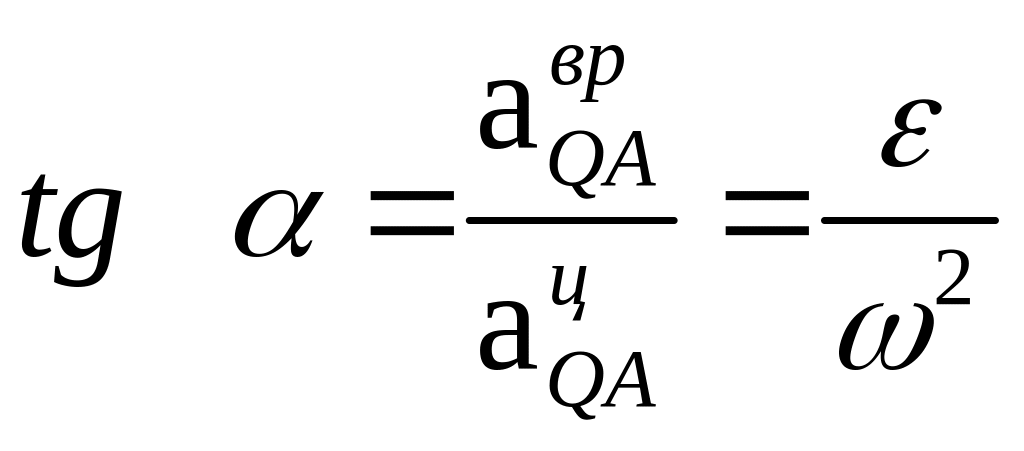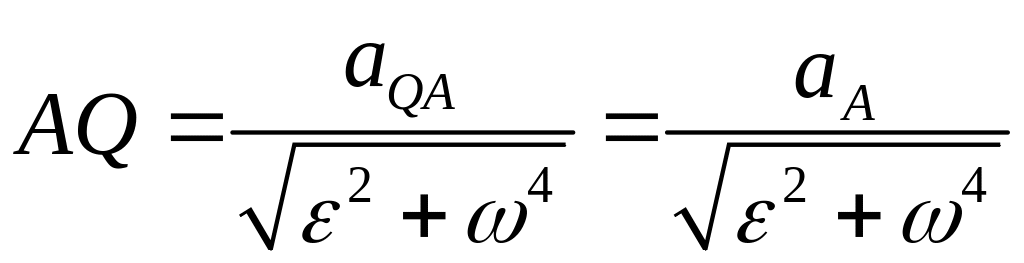Примеры нахождения мцу.

Рассмотрим способы нахождения положения МЦУ.

Пример №1: известны , , (рис.1.16 а).

Определяем угол . Откладываем угол в направлении углового ускорения (т. е. в сторону вращения при ускоренном вращении и против — при замедленном), от направления известного ускорения точки и строим луч. На построенном луче откладываем отрезок длиной AQ.

Рис. 1. 16. Примеры нахождения МЦУ: пример №1 (а), пример№2 (б)

Пример № 2. Известны ускорения двух точек А и В: и (рис.1.16 б).

Одну из точек с известным ускорением принимаем за полюс и определяем относительное ускорение другой точки путём геометрических построений. Измерением находим угол и под этим углом проводим лучи от известных ускорений. Точка пересечения этих лучей является МЦУ. Угол откладывается от векторов ускорений в ту же сторону, в какую идёт угол от вектора относительного ускорения к прямой ВА.

Следует отметить, что МЦУ и МЦС разные точки тела, причём ускорение МЦС не равно нулю и скорость МЦУ не равна нулю (рис 1.17).

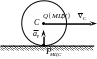
Рис. 1. 17. Положение МЦС и МЦУ в случае качения катка без скольжения

В тех случаях, когда ускорения точек параллельны друг другу возможны следующие частныйслучаи нахождения МЦУ (рис.1.17)

Рис. 1. 18. Частные случаи нахождения МЦУ: а) ускорения двух точек параллельны и равны; б) ускорения двух точек антипараллельны; в) ускорения двух точек параллельны, но не равны

Статика введение в статику Основные понятия статики, область их применения

Статика — раздел механики, изучающий условия равновесия материальных тел и включающий в себя учение о силах.

Говоря о равновесии, надо помнить, что “всякий покой, всякое равновесие относительны, они имеют смысл только по отношению к той или иной определенной форме движения”. Например, тела, покоящиеся на Земле, движутся вместе с ней вокруг Солнца. Более точно и правильно следует говорить об относительном равновесии. Условия равновесия различны для твердых, жидких и газообразных, деформируемых тел.

Большинство инженерных сооружений можно считать малодеформируемыми или жесткими. Абстрагированием можно ввести понятие абсолютно твердого тела: расстояния, между точками которого не изменяются с течением времени.

В статике абсолютно твердого тела решатся две задачи:

• сложение сил и приведение системы сил к простейшему виду;

• определение условий равновесия.

Силы имеют различную физическую природу, часто неясную до конца и в настоящее время. Вслед за Ньютоном, будем понимать силу как количественную модель, меру взаимодействия материальных тел.

Модель силы по Ньютону определяется тремя главными характеристиками: величиной, направлением действия и точкой ее приложения. Опытным путем установлено, что введенная таким путем величина имеет векторные свойства. Более подробно они рассматриваются в аксиомах статики. В международной системе единиц СИ, используемой в соответствии с ГОСТом, единицей измерения силы является ньютон (Н). Изображение и обозначение сил показано на рис.2.1 а

Совокупность сил, действующих на какое-либо тело (или систему тел) называется системой сил.

Тело, не скрепленное с другими телами, которому можно сообщить движение в любом направлении, называется свободным.

Система сил, полностью заменяющая другую систему сил, действующую на свободное тело, не изменяя при этом состояния движения или покоя, называется эквивалентной.

Рис. 2. 1. Основные понятия о силах

Система сил, под действием которой тело может находиться в состоянии покоя, называется эквивалентной нулю или уравновешенной.

Одна сила, эквивалентная системе сил, называется ее равнодействующей. Равнодействующая существует не всегда, например, в случае изображенном на рисунке ее не существует.

Одна сила, равная по величине равнодействующей, но противоположно ей направленная, называется уравновешивающей для исходной системы сил (рис.2.1 б).

Силы, действующие между частицами одного тела, называются внутренними, а действующие со стороны других тел — внешними.