2.2. Изучение темы «Теорема Менелая и теорема Чевы» в курсе геометрии 10 класса.

Профилирование старшей школы предусматривает два курса математики - базовый и профильный. Как уже отмечалось выше, тема « Теорема Менелая и теорема Чевы» изучается лишь в классах физико-математического и естественнонаучного профиля. Причем данный материал «подлежит изучению, но не включается в Требования к уровню подготовки выпускников»[16, с.12], то есть элементы содержания являются обязательными для обучения, однако даются в ознакомительном порядке и не выносятся на итоговый контроль. На изучение темы отводится 2 часа. Распределить материал можно таким образом:

Урок 1.Теорема Менелая и теорема Чевы.

Урок 2. Применение теорем Менелая и Чевы в решении ключевых задач.

Урок 1 по изучению теорем Менелая и Чевы проводится в форме лекции. Основными целями такого урока являются ознакомление учащихся с теоремами и их некоторыми приложениями, повышение познавательного интереса учащихся, выработка у них потребности обобщения изучаемых фактов.

Оборудование: 1. Листы с задачами по теме.

2.Проекционный экран компьютера и слайды, заготовленные на

дискете и проецируемые на экран во время урока.

Ход урока.

Организационный момент - проверить готовность учащихся к уроку.

На проекционном экране (слайд 1) высвечена тема : «Теорема Менелая и теорема Чевы» и эпиграф: «Умение решать задачи - такое же практическое искусство, как умение плавать или бегать. Ему можно научиться только путем подражания или упражнения». (Д.Пойа)

I.Мотивационно - ориентировочная часть.

1. Актуализация знаний.

-В курсе геометрии мы рассматривали важные свойства геометрических фигур на плоскости, в том числе треугольников. Но не все удивительные факты и соотношения вошли в основной курс. А они значительно облегчают решение многих задач. Сегодня мы рассмотрим две теоремы, связанные с отношениями отрезков в треугольнике, и их применение. Но для этого нам потребуются следующие знания:

определение подобных треугольников; признаки подобия; свойства подобных треугольников и их площадей.

Далее идет повторение материала и устная работа со слайдами.

Слайд 2:

;

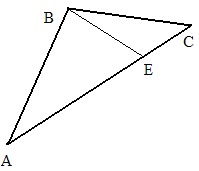
1) Найти 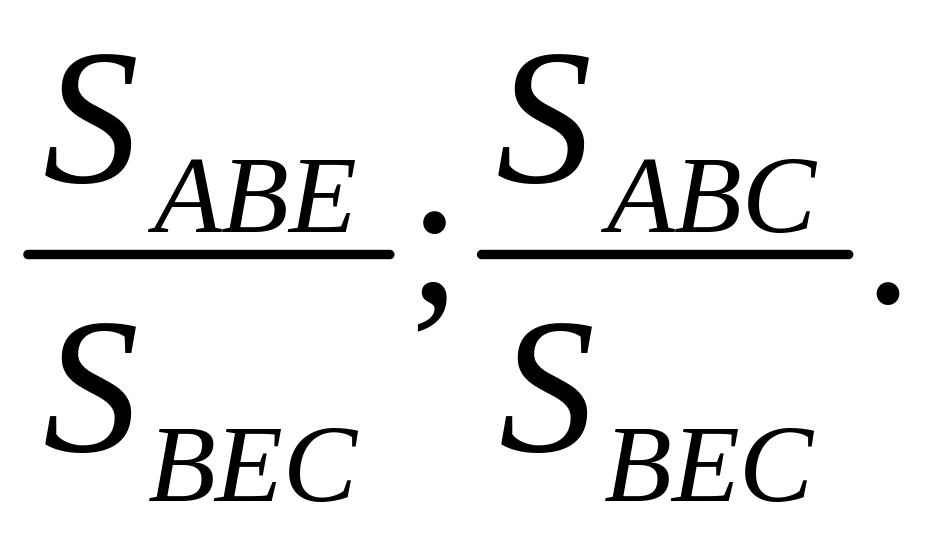2) S =2; S -?

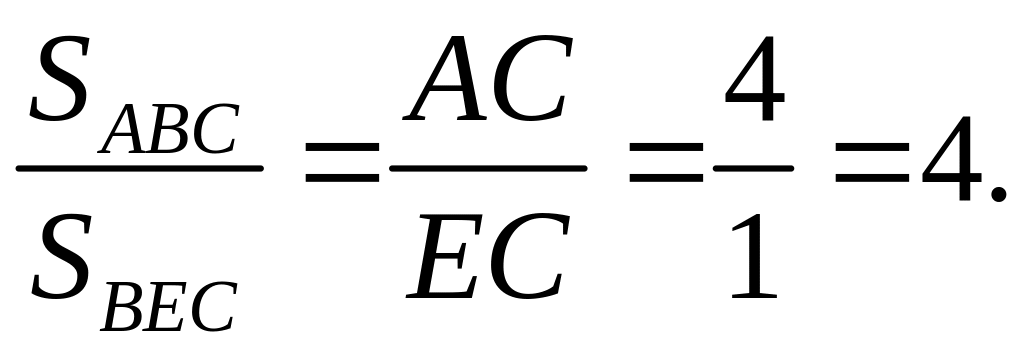Решение. 1) Так как , и имеют одну высоту, проведенную из вершины В, то = =3; 2) .

Слайд 3:

Найти

Решение: общий

2.Мотивация. Постановка учебной задачи.

Ученикам в качестве домашней работы предлагалось решить задачу:

В треугольнике ABC на стороне AC взята точка N так, что AN:NC=m:n, на стороне BC- точка K . BN пересекает AK в точке Q, BQ : QN= p:q. Найти отношение площадей треугольников AKC и ABK.

Идет обсуждение решения задачи. На экране появляется слайд 4.

1) AN:NC=m:n, BQ:QN= p:q, ( т.к. высоты равны)

2) Дополнительное построение: ND||BC.

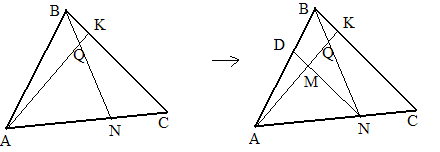
3) ~ по двум углам ;

4) MQN~ KQB по двум углам ; ,

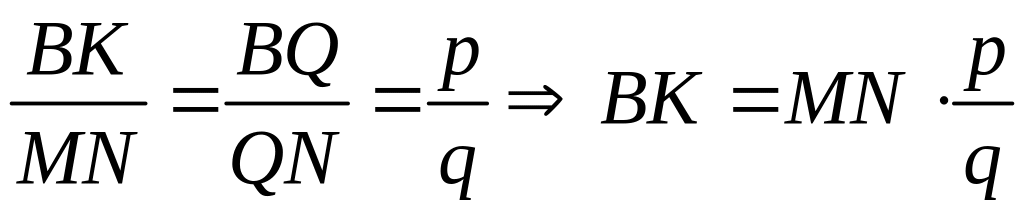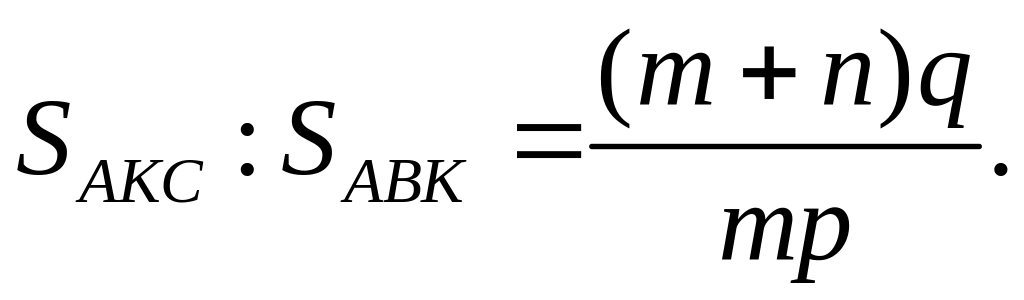
Ответ:

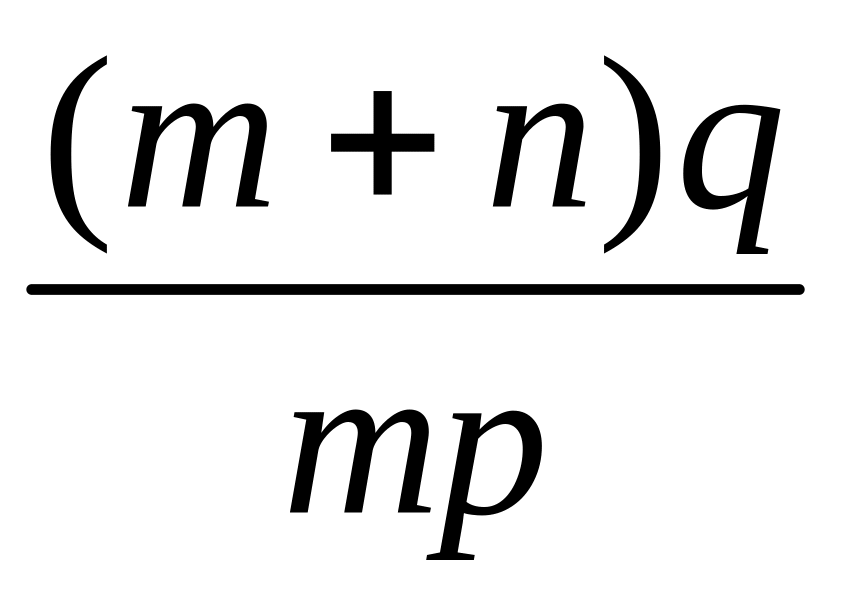
- Эту же задачу можно решить и без дополнительного построения. Быстрый ответ можно получить с помощью теоремы Менелая.

II. Содержательная часть.

Далее идет объяснение нового материала под запись учащихся (см. главу 1). После рассмотрения теоремы возвращаемся к домашней задаче ( слайд 4).

Рассмотрим BCN и секущую AK, K Тогда по теореме Менелая

; ;

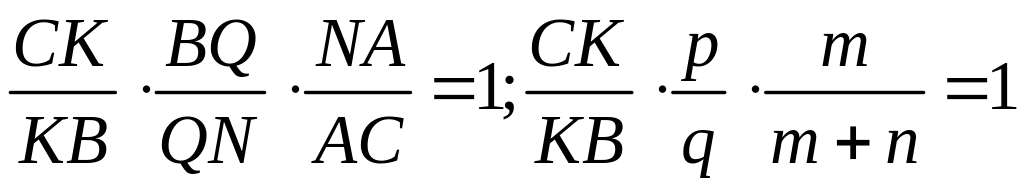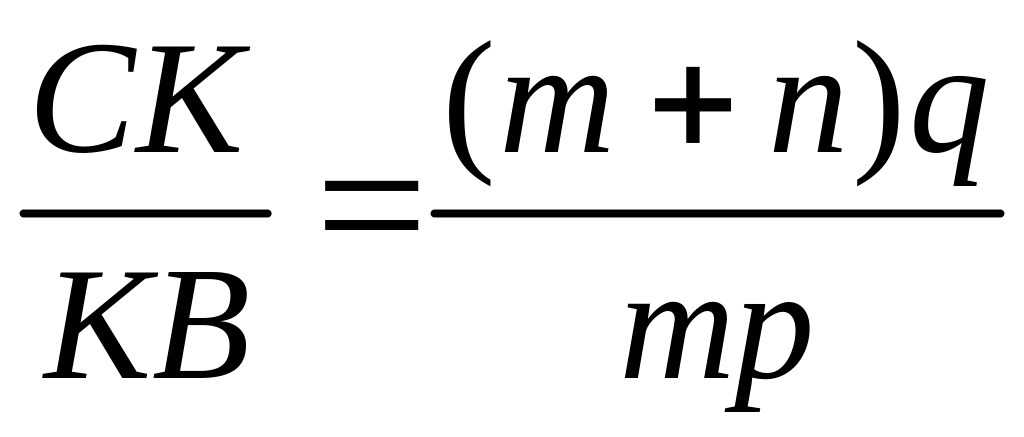Ученикам разъясняется, как правильно выбрать треугольник, как делать его «обход».

Рассматривается еще одна задача.

Слайд 6.

AM= ;

В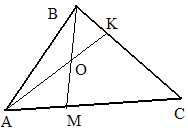 каком отношении отрезок BM делит отрезок AK?

Решение: пусть . Рассмотрим AKC и секущую BM.

По теореме Менелая

Ответ: 2.

Рассмотрим еще одну теорему, связанную с пропорциональными отрезками в треугольнике – теорему Чевы.

Далее дается формулировка и доказательство теоремы для случая внутренней точки (см. главу 1) . Решается задача со слайда 7.

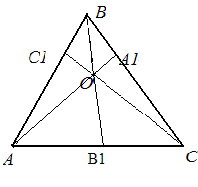
Найти .

Решение: по теореме Чевы для ABC имеем

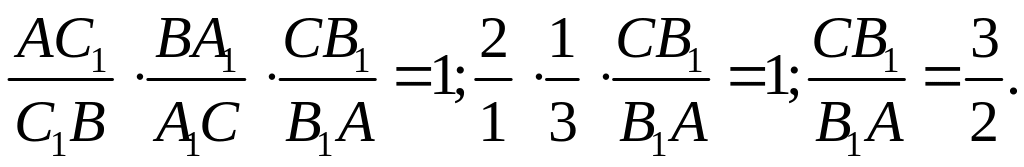
Ответ: =3:2.

III. Рефлексивно – оценочная часть.

Подводятся итоги урока, повторяются утверждения теорем, в листе с задачами по теме отмечаются задачи для домашней работы.

1. В треугольнике ABC на сторонах AB и BC взяты точки K и M; CK AM=O. Обозначим AK: KB= k, BM: MC= m, CO: OK= p, AO:OM= l. Пусть из четырех чисел k,m,p и l известны два. Найти два оставшихся числа, если

а) k=2, m= ; в) k=3, p= 2; д) m= , l= ;

б) k= , m= ; г) k=2, l=3; е) p=2, l=1.

Ответы: а) p= , l= ; б) p=5, l=1; в) m= , l=5; г) m= , p=3; д) k= , p=15; е) k= , m=2.

5. На сторонах AC и BC ABC расположены соответственно точки N и M так, что AN:NC=k, BM:MC=m, прямые AM и CM пересекаются в точке O. Найти отношения

AO:OM, BO:ON. Ответ:

Урок 2 .Тема «Применение теорем Менелая и Чевы в решении ключевых задач».

Цели урока: формировать умения:

-видеть конфигурации, удовлетворяющие заданным условиям;

-решать задачи нестандартными способами;

-осуществлять поиск решения комплексных задач синтетическим методом;

-использовать теоремы в задачах на доказательство;

-развивать самостоятельность.

Ход урока.

I. Мотивационно – ориентировочная часть.

1. Актуализация знаний.

В начале урока повторяются формулировки изученных теорем. В качестве устного упражнения можно предложить выполнить следующее задание:

На следующих рисунках указать треугольник, секущую и точки ее пересечения с каждой стороной треугольника или продолжением:

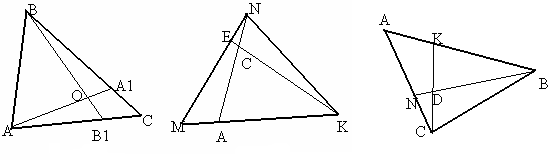
Д алее класс делится на 4 группы, решается задача 1.

В ABC на сторонах AB, BC,AC взяты точки C , A ,B соответственно. Отрезки BB ,AA , CC пересекаются в точке O. CB : B A=p, CA : A B=q.

Найти : .

Каждая группа находит одно из указанных отношений, далее идет проверка результатов.

Учитель выборочно оценивает работы учеников.

2. Мотивация. Постановка учебной задачи.

Мы рассмотрели задачи на прямое применение теорем Менелая и Чевы.

На этом уроке мы научимся применять эти утверждения к задачам, в которых первоначально не указано отношение отрезков и рассмотрим утверждения, обратные теоремам Менелая и Чевы.

I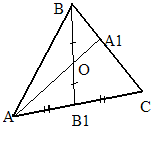 I. Содержательная часть.

Рассмотрим следующие задачи.

Задача2.В каком отношении делит сторону BC треугольника ABC прямая, проходящая через точку A и середину медианы, выходящей из B?

Задача 3.

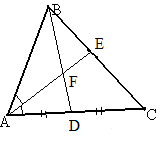Дано:

ABC; AE - биссектриса,

BD - медиана ; AB=2, AC=3;

Найти BF: FD

Ввиду того, что задачи эти были решены выше, здесь их решение опускаем.

Далее ставится вопрос о справедливости обратных утверждений. Записываются формулировки теорем, обратных теоремам Менелая и Чевы. Используя их, предложить доказать известное утверждение: Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

III. Рефлексивно – оценочная часть.

1. Подведение итогов.

Итогом может служить небольшая проверочная работа, организовать которую поможет таблица (с.24). Два отношения в каждой задаче учитель задает учащимся, остальные они находят самостоятельно.

2. Домашнее задание.

1) Используя теоремы Чевы и Менелая, доказать, что биссектрисы треугольника пересекаются в одной точке.

2) Доказать, что высоты треугольника или их продолжения пересекаются в одной точке.

3)Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник.

Примечание : в зависимости от уровня подготовленности класса и при наличии времени учитель может провести урок-практикум решения задач, включив комбинированные задачи (см.п.2.1), которые будут также полезны учащимся, так как они способствуют обобщению методов, приемов решения задач темы.

Также в 10 классе при изучении темы «Задачи на построение сечений» в параграфе «Тетраэдр и параллелепипед» можно использовать задачи типа

В тетраэдре ABCD на ребрах AB, BD, DC взяты точки K,M,P соответственно так, что Через точки K,M и P проходит плоскость, пересекающая прямые AD,BC и CA в точках E,F и G. Найти Какие из точек E, F и G расположены на ребрах тетраэдра?