Глава 2. Методические рекомендации к изучению темы в

школьном курсе геометрии.

Обучение решению геометрических задач с применением теорем Менелая и Чевы проводим в 3 этапа:

1 этап – в период предпрофильной подготовки, в 8-9 классах, знакомим учащихся с теоремами и формируем умения решать ключевые задачи темы;

2 этап – рассматриваем соответствующие вопросы в школьном курсе геометрии 10 класса профильного уровня;

3 этап – после изучения основ стереометрии показываем, как «работают» теоремы в решении стереометрических задач, включая конкурсные задачи вступительных экзаменов в вузы.

2.1 Методика обучения решению задач с применением теорем Менелая и Чевы в период предпрофильной подготовки.

К моменту изучения темы учащиеся должны знать теорему Фалеса, формулу вычисления площади треугольника и свойства площадей треугольников, свойство биссектрисы треугольника, признаки подобия треугольников, теоремы о пересечении биссектрис, медиан, серединных перпендикуляров, высот в треугольнике. Этот материал изучается в 8 классе. Поэтому в 9 классе в рамках факультатива «За страницами учебника» отводим 10 часов на тему «Некоторые замечательные теоремы планиметрии», в которой рассматриваем следующие вопросы:

1. Теорема Менелая и пропорциональные отрезки в треугольнике (2 часа).

2. Теорема Чевы и ее следствия. Применение теорем Чевы и Менелая к задачам на доказательство(2 часа).

3. Решение задач на пропорциональное деление отрезков в треугольнике.(2 часа).

4. Решение задач, связанных с нахождением площадей (2 часа).

5. Комбинированные задачи (2 часа).

Каждое занятие, а также все они в целом направлены на то, чтобы развить интерес учащихся к предмету, познакомить с новыми идеями и методами, расширить представления об изучаемом в основном курсе материале, а главное, порешать интересные геометрические задачи алгебраическим способом.

Занятия 1-2. Тема: Теорема Менелая и пропорциональные отрезки в треугольнике.

В результате изучения материала этих занятий учащиеся должны:

знать формулировки теоремы Менелая и теоремы, обратной теореме Менелая;

уметь воспроизводить доказательство теоремы Менелая и применять ее при решении простейших задач.

В начале занятия 1 необходимо повторить основные теоретические сведения, связанные с треугольником, известные учащимся с 7-8 классов. Затем предложить решить задачу 1:

В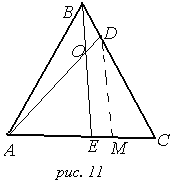 треугольнике ABC точка D делит сторону BC в отношении BD:DC= 1: 3, а точка O делит AD в отношении AO:OD=5:2. В каком отношении прямая BO делит отрезок AC?

Дано:

ABC, D BC, BD: DC= 1:3

O AD, AO: OD= 5:2

BO AC= E

Найти AE: EC

Решение:

Проведем DM ll BE (рис. 11). По теореме Фалеса . Тогда AE= 5k , EM= 2k, где k- коэффициент пропорциональности. Аналогично , откуда MC= 3EM=6k; EC= 2k+6k= 8k; .

Ответ: AE: EC= 5:8

Для решения этой задачи пришлось выполнить дополнительное построение. Вряд ли учащиеся смогут догадаться, какое именно дополнительное построение требуется для решения этой или похожей задачи, поэтому она может оказаться сложной для них.

Можно сообщить ученикам, что эту задачу можно решить без дополнительного построения, причем достаточно просто и быстро. Но для этого нам понадобится следующее утверждение - и далее идет знакомство с теоремой Менелая, но ее формулировка (с.9) разбивается на 2 независимых утверждения - прямую и обратную теоремы.

Теорема (Менелая). Пусть на сторонах AB,BC и на продолжении стороны AC ABC взяты соответственно точки C ,A и B , не совпадающие с вершинами треугольника. Если точки A ,B ,C лежат на одной прямой, то выполняется равенство

. . =1 ( )

Доказательство теоремы проводится одним из способов, рассмотренных в главе 1 на с.10-11.

Необходимость рассмотрения случая, когда точки A ,B ,C лежат на продолжениях сторон треугольника, определяет учитель. Нужно сообщить учащимся, что при составлении равенства ( ) надо переходить от вершины к вершине через точку пересечения секущей линии с этой стороной или ее продолжением; заканчивать необходимо в той же вершине, с которой начали; равенство Менелая можно записывать, начиная с любой вершины треугольника в любом направлении (по часовой стрелке, против часовой стрелки). После рассмотрения теоремы Менелая возвращаемся к решению задачи 1.

Рассмотрим ADC; B DC,O AD, E AC; O,B,E лежат на одной прямой; по

теореме Менелая . . =1. Так как BD: DC= 1:3, то CB: BD=4:1,

подставляем, получаем . . =1, = .

Таким образом, сопоставление разных способов решения может оказаться весьма полезным, становится очевидным преимущество второго способа.

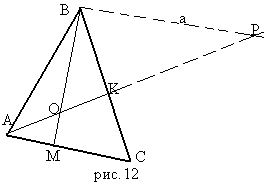
Рассмотрим задачу 2.

В ABC на стороне AC взята точка M, а на стороне BC – точка K так, что AM: MC= 2:3, BK: KC= 4:3. В каком отношении AK делит отрезок BM?

Решение:

I способ. Через точку B проведем прямую a ll AC (рис.12); AK a=P;

BKP ~ CKA BP= AC.

BOP~ MOA ~ =

Ответ: = .

В этом случае нужно увидеть подобные треугольники, для чего использовать дополнительное построение.

II способ. Рассмотрим MBC; прямую AK назовем секущей, так как она пересекает две стороны и продолжение третьей стороны треугольника MBC; A MC,O BM, K BC;

A,O,K лежат на AK ( на одной прямой). По теореме Менелая , , = .

Замечаем, что теорема Менелая проста для применения, но здесь важно увидеть нужную конфигурацию - треугольник и секущую, причем такие, что два отношения в равенстве Менелая будут известны, тогда можно будет найти третье. В связи с этим полезны упражнения «на узнавание»:

На следующих рисунках указать треугольник, секущую и точки ее пересечения с каждой стороной треугольника или продолжением:

З адача 3. В каком отношении делит сторону BC треугольника ABC прямая, проходящая через точку A и середину медианы, выходящей из B?

Дано:

ABC; AB = B C; BO=OB ;

Найти BA : A C

Решение:

Рассмотрим BCB и секущую AA ; A B C, O BB , A BC.

По теореме Менелая ; ; =

Ответ: BA : A C=1:2

Задача 4. Дано:

ABC; AA - биссектриса,

BB - медиана; AB=2, AC=3;

Найти BO: OB

Решение:

AA - биссектриса = .

Рассмотрим BB C и секущую AA ; A B C, A BC, O BB (рис.17).

По теореме Менелая

; .

Ответ: BO: OB =4:3

Задача 5. На сторонах AC и BC ABC отмечены соответственно точки N и K так, что AN: NC= m : n, AK BN= Q, BQ: QN= p : q. Найти BK: KC.

Решение:

Рассмотрим BCN и секущую AK; A NC, Q BN, K BC (рис. 18).

По теореме Менелая

Ответ :

Далее ставим вопрос о справедливости обратного утверждения.

Теорема (Менелая, обратная). Пусть дан треугольник ABC. Предположим, что точка C лежит на стороне AB, точка A лежит на стороне BC, а точка B лежит на продолжении стороны AC, причем про эти точки известно, что . . =1 . Тогда эти точки лежат на одной прямой.

Доказательство этого утверждения приводится в главе 1, с.11.

Задачи для самостоятельного решения:

1. В треугольнике ABC на сторонах AB и BC взяты точки K и M , KM AC= P. Найти CP: AP, если а) AK: KB= 2, BM: MC= 1:3;

б) AK: KB= 3, BM: MC = 4;

в) AK: KB= 2:5, BM: MC = 2.

Ответы: а) 3:2; б) 1:12; в) 5:8.

2. В треугольнике ABC на сторонах AB и BC взяты точки K и M; CK AM=O. Обозначим AK: KB= k, BM: MC= m, CO: OK= p, AO:OM= l. Пусть из четырех чисел k,m,p и l известны два. Найти два оставшихся числа, если

а) k=2, m= ; в) k=3, p= 2; д) m= , l= ;

б) k= , m= ; г) k=2, l=3; е) p=2, l=1.

Ответы: а) p= , l= ; б) p=5, l=1; в) m= , l=5; г) m= , p=3; д) k= , p=15; е) k= , m=2.

3. В треугольнике ABC на стороне AC взята точка M такая, что AM= AC, а на стороне BC – точка K такая, что BK= BC. В каком отношении отрезок BM делит отрезок AK?

4. На сторонах AB и BC треугольника ABC взяты соответственно точки K и M так, что AK:AB= BM: BC= 1:3. В каком отношении точка пересечения CK и AM делит каждый из этих отрезков?

5. На сторонах AC и BC расположены соответственно точки N и M так, что AN:NC=k, BM:MC=m, прямые AM и BN пересекаются в точке O. Найти отношения AO:OM, BO:ON.

Занятия 3-4. Тема: Теорема Чевы и ее следствия. Применение теоремы Чевы и теоремы Менелая к задачам на доказательство.

Цели: рассмотреть теорему Чевы, утверждение которой также связано с отрезками в треугольнике, некоторые следствия из нее; показать, как теоремы Чевы и Менелая применяются в задачах на доказательство.

Формулировка теоремы Чевы включает два взаимно обратных утверждения. Их можно рассмотреть как независимые теоремы.

Теорема (Чевы). Пусть точки A ,B , C лежат соответственно на сторонах BC,AC и AB треугольника ABC, причем отрезки AA , BB ,CC пересекаются в одной точке.

Тогда . . =1

Доказательство теоремы проводится одним из способов, предложенных в главе I на с.6.

Исследование остальных случаев расположения точек - по усмотрению учителя, но в любом случае целесообразно сформулировать теорему Чевы и для случая внешней точки пересечения AA , BB ,CC и для случая параллельных прямых, а также рассмотреть обратное утверждение.

Теорема (Чевы, обратная). Пусть точки A ,B , C лежат соответственно на сторонах BC,AC и AB треугольника ABC, причем . . =1. Тогда отрезки AA , BB ,CC пересекаются в одной точке.(Остальные случаи разъяснить).

Задача.

Н а сторонах треугольника ABC взяты соответственно точки C , A ,B ,так, что AC : С B= 2:1, BA :A C=1:3,

BB CC AA =O. Найти CB : B A.

Решение:

Так как отрезки BB , CC , AA пересекаются в одной точке O, то по теореме Чевы . . =1; =1; =

Ответ: 3:2

Далее рассматриваются некоторые следствия из теоремы Чевы.

С ледствие1.Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

Доказательство. В учебной литературе доказательство этого утверждения проводится на основе подобных треугольников. Мы же проведем его, опираясь на теоремы Чевы и Менелая. Итак, пусть AA , BB ,CC - медианы ABC (рис.20) . Так как AC =C B, BA =A C, AB =B C, то =1, = 1, =1. Тогда . . , т.е. для точек A ,B ,C , лежащих на сторонах треугольника ABC, выполняется условие ( ) ; по теореме Чевы AA , BB ,CC пересекутся в одной точке O (случай внутренней точки).

Рассмотрим B BC , точки A,O,A лежат на одной прямой, пересекающей стороны BB ,BC и продолжение стороны B C (в дальнейшем будем называть ее секущей). A B C, O BB , A BC.

По теореме Менелая , = .

Применяя теорему Менелая для A AC и секущей BB (B A C, O AA , B AC), получим, что = ; применяя теорему Менелая для С BC и секущей AA , получим, что . Утверждение доказано.

Следствие 2. Биссектрисы треугольника пересекаются в одной точке.

Доказательство. Справедливость этого утверждения можно доказать, используя свойство биссектрисы:

так как AA - биссектриса, то = ; так как BB - биссектриса, то ;

так как СС - биссектриса, то . Перемножая соответственно левые и правые части этих равенств, получим . . = . . =1, то есть для точек A , B , C выполняется равенство Чевы, значит, AA , BB ,CC пересекаются в одной точке.

Примечание 7: если учащимся известна теорема Чевы в форме синусов, то провести доказательство этого следствия можно следующим образом. Пусть AA ,BB ,CC - биссектрисы ABC (рис.21) Так как , то = 1; аналогично, =1; =1.

П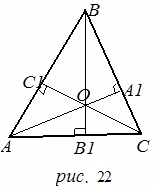 еремножая эти равенства, получим условие ( ) теоремы Чевы в форме синусов. Значит, AA , BB ,CC пересекаются в одной точке.

Следствие3. Высоты треугольника (или их продолжения) пересекаются в одной точке (ортоцентре треугольника).

Доказательство: пусть AA , BB ,CC - высоты ABC .

1) Если ABC остроугольный (рис. 22), то точки A , B , C лежат на его сторонах. ACC -прямоугольный, AC = AC cosA;

BCC - прямоугольный, BC = BC cosB; BA A – прямоугольный, BA = AB cosB;

AA C- прямоугольный, A C=AC cosC; CB =CB cosC; AB = AB cosA.

Тогда . . = =1. А так как условие ( ) выполняется, то AA , BB , CC пересекаются в одной точке.

Примечание 8: следствие 3 можно доказать, исходя из подобия треугольников. Можно предложить учащимся провести доказательство этим способом самостоятельно. (Действительно, AA C~ BB C по I признаку ; аналогично, из подобия CC B и AA B следует, что . И, наконец,

BB A ~ CC A . Перемножая эти равенства, получим

. Отсюда по теореме Чевы следует, что высоты остроугольного треугольника пересекаются в одной точке.[4, с.96])

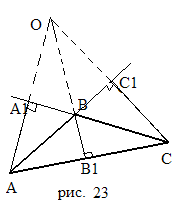
2) Пусть ABC – тупоугольный (рис.23). Это случай внешней точки O. Из ACC AC =ACcosA; из С BC C B=CB cos (180 - B)= -CB cosB ( угол B тупой) ;

из A BA BA =AB cos(180 - B)=-AB cosB; аналогично,

AB =AB cosA; B C= BC cosC; A C= AC cosC; CB =CBcosC.

.

Т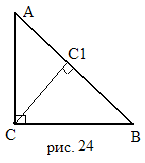 ак как условие Чевы выполняется, то AA , BB , CC пересекаются в одной точке или параллельны (глава1). Но если бы они были параллельны, то и перпендикулярные к ним прямые, то есть стороны треугольника ABC, были бы параллельны друг другу, но это не так. Значит, прямые AA ,BB ,CC пересекаются в одной точке.

3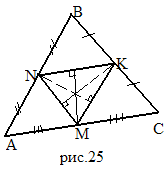 ) Если ABC прямоугольный, С=90 (рис.24) , то очевидно, что высоты BC,AC,CC пересекаются в точке С. Следствие 3 доказано.

Следствие4. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство. Рассмотрим серединный MNK(вершины-середины сторон ABC)(рис.25). Тогда NK,NM,MK – средние линии треугольника ABC и по свойству средней линии NK AC, NM BC, KM AB. Поэтому серединные перпендикуляры к сторонам треугольника ABC содержат высоты MNK. А в MNK по следствию 3 высоты пересекаются в одной точке, следовательно, серединные перпендикуляры пересекаются в одной точке.

Таким образом, теорема Чевы дает возможность весьма просто доказать известные утверждения о четырех замечательных точках треугольника.

Рассмотрим еще одно следствие из теоремы Чевы.

С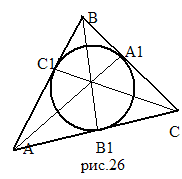 ледствие 5. Прямые, соединяющие вершины треугольника с точками, в которых вписанная окружность касается противоположных сторон, пересекаются в одной точке. Эта точка называется точкой Жергонна (рис.26).

Доказательство. По свойству отрезков касательных, проведенных к окружности из одной точки, имеем AB =AC =x, C B=BA =y, A C=B C=z.

, по теореме Чевы AA , BB , CC пересекаются в одной точке.

Дополнительные задачи:

1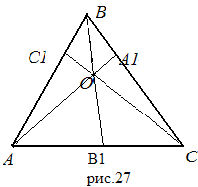 . Используя теорему Чевы, доказать, что в произвольном треугольнике прямые, проходящие через вершины и делящие периметр треугольника пополам, пересекаются в одной точке.[4, с.94]

Доказательство: Пусть каждый из отрезков AA , BB ,CC делит периметр треугольника ABC пополам (рис.27), то есть AB+BA =A C+AC(1), B C+BC=AB +AB(2), AC + СA=

=C B+BC (3)

Сложим (1), (2), (3): AB+BA +B C+BC+AC +CA= A C+AC+ AB +AB+ C B+BC; BA +B C+AC =A C+AB +C B. Перенесем слагаемые в левую часть и сгруппируем:

(BA - AB ) + (B C - C B) + (AC - A C)=0 (4). Вычитая из (1) равенство (2), получаем :

(AB+BA )- (AB +AB) = (A C+AC)-( B C+BC) или BA - AB = (AC- B C)-(BC- A C)=AB - BA = -( BA - AB ), откуда 2(BA - AB )= 0, BA = AB .

Аналогично доказывается, что CB = С B , C A = A C.

Тогда . . .

По теореме Чевы AA , BB ,CC пересекаются в одной точке.

2 . На стороне AC треугольника ABC взяты точки P и E , на стороне BC – точки M и K, причем AP: PE: EC= CK: KM: MB. Отрезки AM и BP пересекаются в точке O, отрезки AK и BE – в точке T. Докажите, что точки O, T и С лежат на одной прямой.[4, с.94]

Дано:

ABC; AP: PE: EC= CK: KM: MB=m:n:k

M, K BC, P, E AC; AM BP= O;

AK BE= T

Доказать: O, T, C a

Доказательство. Пусть луч CT AB=C , CO AB=C . Докажем, что точки C и C совпадают, это и будет означать, что O, T, C лежат на одной прямой.

Так как CT AB=C , BE AK CC = T, то по теореме Чевы ;

(1)

Так как CO AB=C , AM BP= O, то СС BP AM=O, по теореме Чевы (2)

Из (1) и (2) следует, что , то есть точки С и C делят отрезок AB в одном и том же отношении, начиная от точки A, а значит, С и C совпадают. А это означает, что точки O, T, C лежат на одной прямой.

3. Прямая пересекает стороны AB,BC и продолжение стороны AC треугольника ABC соответственно в точках D,E,F.Доказать, что середины сторон отрезков DC, AE и BF лежат на одной прямой.(Теорема Гаусса.) Указание: воспользоваться теоремой Менелая, в качестве вершин данного треугольника взять середины сторон треугольника ABC, на сторонах и продолжениях которого лежат рассматриваемые точки.

4. Треугольники ABC и A B C с попарно непараллельными сторонами расположены так, что прямые AA и A BB пересекаются в одной точке O. Доказать, что точки M,K,P пересечения прямых AB и A B , BC и B C , AC и A C соответственно лежат на одной прямой. (Теорема Дезарга.) Указание: воспользоваться теоремой Менелая.

Задачи для самостоятельного решения.

1. Доказать, что середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон лежат на одной прямой. Указание: дважды используя теорему Менелая, доказать, что прямая, проходящая через точку пересечения диагоналей трапеции и через точку пересечения продолжений боковых сторон, проходит через середины оснований.

2. Доказать, что: а) биссектрисы внешних углов треугольника пересекают продолжения противоположных сторон треугольника в трех точках, расположенных на одной прямой; б) касательные к описанной около треугольника окружности в вершинах треугольника пересекают его противоположные стороны в трех точках, расположенных на одной прямой. Указание: воспользоваться теоремой Менелая.

3. На сторонах AB, BC и CA треугольника ABC взяты точки C ,A и B соответственно. Пусть C - точка пересечения прямых AB и A B , A - точка пересечения прямых BC и B C , B - точка пересечения прямых AC и A C . Доказать, что если прямые AA , BB , CC пересекаются в одной точке, то точки A , B , C лежат на одной прямой. Указание: записав равенство Чевы для точек A ,B ,C ; A ,B , C ; A , B , C ; A , B ,C ,получить, что для точек A , B , C выполняется равенство Чевы ; далее доказать, что или все три точки A , B , C лежат на продолжениях сторон треугольника( так будет, если A ,B ,C лежат на сторонах треугольника), или лишь одна находится на продолжении (если на сторонах треугольника одна из точек A ,B ,C ) и воспользоваться теоремой Менелая.

4. Пусть ABCD – четырехугольник, P- точка пересечения BC и AD, Q – точка пересечения AC и BD, R – точка пересечения AB и CD. Доказать, что точки пересечения BC и QR, CA и RP, AB и PQ лежат на одной прямой. Указание: применить теорему Менелая к треугольникам ABD,BDC и DCA.

5. Окружность пересекает сторону AB треугольника ABC в точках C и C , сторону BС – в точках A и A , сторону CA- в точках B и B . Доказать, что если прямые AA ,BB и CC пересекаются в одной точке, то и прямые AA , BB и CC также пересекаются в одной точке. Указание: воспользоваться теоремой Чевы.

Занятия 5-6. Тема: Решение задач на пропорциональное деление отрезков в треугольнике.

Цели: овладение навыком решения задач с использованием теорем Менелая и Чевы; повышение уровня математической культуры учащихся, развитие их познавательных способностей.

Прежде всего надо отметить, что усвоение каждой темы школьного курса математики и развитие учащихся на том или ином уровне обеспечивается определенной системой упражнений и задач. [7,с.203] Выполнение математических упражнений является важнейшим видом учебной деятельности, в процессе которой школьниками усваивается математическая теория, развиваются их творческие способности и самостоятельность мышления.[15,с.3] Умение решать задачи самостоятельно, без посторонней помощи формируется автоматически, непроизвольно лишь у небольшой части учащихся. Для большинства же требуется специальная работа учителя в этом направлении. У школьников необходимо формировать умение решать и стандартные, и нестандартные задачи.

Наработать навыки решения стандартных задач на применение теорем Чевы и Менелая , а также организовать контроль за их выполнением поможет следующая таблица.

Отнош. № зад.	а)	б)	в)	г)	д)	е)
1.
2.
3.
4.
5.
6.
7.
8.

Если три отрезка, соединяющие вершины A,B,C треугольника соответственно с точками A ,B ,C лежащими на его сторонах, противоположных этим вершинам, пересекаются в точке O, то по любым двум из шести отношений длин отрезков, на которые точки A ,B ,C делят стороны треугольника, а точка O- отрезки AA ,BB ,CC , однозначно определяются оставшиеся отношения(с помощью теорем Менелая и Чевы).

Д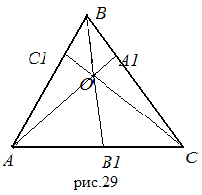 ве задачи из таблицы можно разобрать на занятии, остальные дать домой (используя таблицу, можно составить несколько вариантов заданий).

Далее можно организовать работу в группах.

Задача.

В ABC на сторонах AB, BC,AC взяты точки C , A ,B соответственно. Отрезки BB ,AA , CC пересекаются в точке O. CB : B A=p, CA : A B=q.

Найти : .

Ученики делятся на 4 группы по количеству отношений, которые необходимо найти.

После того как задача окажется решена каждой группой, идет выступление представителей.

Решение: 1) Рассмотрим ; O AA , B A C, B AC, O,B,B лежат на одной прямой (рис.29).

По теореме Менелая ; .

2) Рассмотрим ; O BB , A BC, A CB ; O, A ,A лежат на одной прямой.

По теореме Менелая ; .

3) Рассмотрим , по теореме Чевы ; ; .

По теореме Менелая для СС A и секущей BB ; ; .

4) Рассмотрим , по теореме Чевы ; ; .

Чтобы включить знания учащихся в систему, важно среди задач по теме иметь комплексные задачи, то есть задачи, при решении которых используются знания, полученные при изучении не только данной, но и предыдущих тем, а также при изучении других разделов математики. Поэтому полезными окажутся задачи 1-5.

З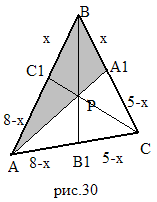 адача 1. .В треугольнике ABC, описанном около окружности, AB = 8, BC = 5, AC = 4. Точки A ,В и C - точки касания, принадлежащие соответственно сторонам BC,AC и BA. Точка P - точка пересечения отрезков AA и CC .

Найдите AP: PA .

Решение: так как отрезки, соединяющие вершины треугольника с точками касания противоположных сторон, пересекаются в одной точке, то P BB . Пусть C B=x, тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения ( рис. 30)

8 - x + 5 - x = 4, x = . Значит,C B = BA= ; A C = 5 – = , AC = 8 – = .

В треугольнике ABA прямая C C пересекает две его стороны и продолжение третьей стороны. По теореме Менелая

, , = .

Ответ: 70: 9.

Задача 2. Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник.

Р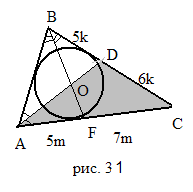 ешение: пусть в треугольнике ABC AB = 5, BC = 7, AC = 6. Угол BAC лежит против большей стороны в треугольнике ABC, значит, угол BAC – больший угол треугольника. Центр вписанной окружности треугольника лежит на пересечении биссектрис. Пусть O -точка пересечения биссектрис. Необходимо найти AO:OD. Так как AD – биссектриса треугольника ABC, то = , то есть BD = 5k, DC = 6k. Так как BF – биссектриса треугольника ABC, то = , то есть AF = 5m, FC = 7m.

Прямая BF пересекает две стороны и продолжение третьей треугольника ADC.

По теореме Менелая

. . = 1, = = =

Ответ: 11:7.

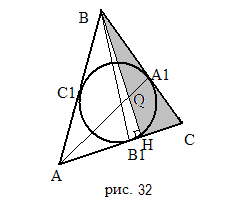Задача 3. В треугольнике ABC, описанном около окружности, AB =13, BC = 12, AC = 9, A и C - точки касания, лежащие соответственно на сторонах BC и AB. Q –точка пересечения отрезков AA и BH,где BH- высота. Найдите отношение BQ:QH.

Решение:

треугольник ABC – разносторонний, значит, точка H не совпадает с точкой касания. Обозначим точку касания, лежащую на стороне AC, буквой B .

1. Пусть C B = x, тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (рис.32):

BA =x, A C=B C=12-x, AC =AB =13-x. Тогда (13 – x) + (12 – x) = 9, x=8. Значит, C B =BA = 8, AC =AB = 5, CA =CB =4.

2. По формуле Герона

S = = 4 ,

S = , BH= , BH = .

3. Из треугольника ABH (прямоугольного) по теореме Пифагора

AH = = .

4. В треугольнике CBH прямая AA пересекает две его стороны и продолжение третьей. По теореме Менелая

. . =1, . . =1, . . =1, = .

Ответ: 162:53.

З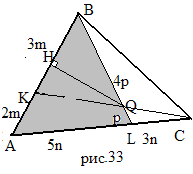 адача 4. В треугольнике ABC, площадь которого равна 6, на стороне AB взята точка K, делящая эту сторону в отношении AK:BK = 2:3, а на стороне AC – точка L, делящая AC в отношении AL: LC = 5:3. Точка Q пересечения прямых CK и BL удалена от прямой AB на расстояние . Найдите длину стороны AB.

Решение:

1. Треугольники ABL и ABC имеют одинаковую высоту, проведенную из вершины B.

= = = , тогда S = 6 = .

2. Прямая KC пересекает в треугольнике ABL две стороны и продолжение третьей. По теореме Менелая

. . = 1, . . = 1, = , то есть BQ = 4p, QL = p.

3. Треугольники KBQ и ABL имеют общий угол, значит,

= = = , тогда S = . = .

4. S = KB = = , 3m = , тогда m = , AB=5m = 4.

Итак, AB = 4.

Ответ: 4.

Задача 5. На стороне AC в треугольнике ABC взята точка K. AK = 1, KC = 3. На стороне AB взята точка L. AL:LB=2:3. Q – точка пересечения прямых BK и CL. S = 1. Найдите длину высоты треугольника ABC, опущенной из вершины B.

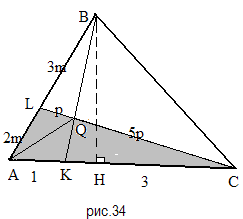
Решение: прямая BK пересекает две стороны и продолжение третьей треугольника ALC (рис.34) . По теореме Менелая

, , то есть LQ = 1p, QC = 5p.

1) треугольники ALC и AQC имеют общий угол, значит,

, S = .

2) Треугольники ABC и ALC имеют общую высоту, проведенную из вершины C, значит,

, S = .

3) S = , BH = .

Ответ:1,5.

Для самостоятельного решения можно взять задачи 3-8 из таблицы.

Занятия 7-8. Тема: Решение задач, связанных с нахождением площадей.

Многие планиметрические задачи заканчиваются словами «найти площадь…». Примерно половина из них может быть решена посредством нахождения отрезков и углов, необходимых для вычисления площади данной фигуры; часто в таких задачах бывает удобным и метод поиска площадей фигур путем сравнения с известными площадями.

Рассмотрим ряд таких задач и возможность использования в них известных нам теорем.

З адача 1. На сторонах AC и BC треугольника ABC отмечены точки N и K так, что AN:NC=m:n, AK BN=Q, BQ:QN=p:q. Найти отношение площадей треугольников AKC и ABK.

Решение: AKC и ABK имеют одинаковую высоту,

проведенную из вершины A, поэтому (рис.18).

По теореме Менелая для BCN и секущей AK имеем ; . Отсюда

. Ответ:

З адача 2. Через вершину B проведена прямая, параллельная биссектрисе С и пересекающая продолжение стороны АС в точке D. Пусть Е – середина отрезка ВD. Определить, в каком отношении прямая АЕ делит площадь , если известно, что АС=5, ВС=10.

Решение: 1) СК – биссектриса .

2) ~ по двум углам , .

Рассмотрим и секущую АЕ; A CD, F BC, E BD, A,F,E AE.

По теореме Менелая , , .

Ответ: 1:3.

Задача 3. Медиана BD и биссектриса AE треугольника ABC пересекаются в точке F. Найти площадь треугольника ABC , если AF=3FE, BD=4, AE=6.

Решение: пусть FE=k, тогда AF=3k. AE=AF+FE= 3k+k=4k, 4k=6, k= . AF= FE= .

Рассмотрим и секущую BD; B EC, F AE, D AC. По теореме Менелая .

Рассмотрим и секущую АЕ; А DC, F BD, E BC, A,F,E AE.

По теореме Менелая .

В AF – биссектриса и медиана - равнобедренный и ;

; .

Ответ: 18

З адача 4. В равнобедренном треугольнике ABC (AС=BC) проведены медиана BN и высота АМ, которые пересекаются в точке D. AD=5, DM=2. Найти .

Решение: AN=NC, AM=5+2=7. Рассмотрим AMC и секущую NB (рис. 37)

N AC, B CM, D AM. По теореме Менелая ; ; .

Пусть коэффициент пропорциональности равен k, тогда СМ=3k, BM=2k.

Из ACM - прямоугольного: ,

;

; , ,

Тогда ,

Ответ: .

З адача 5. В ABC на сторонах AB и BC взяты точки K и L так, что и , , . Найти .

Решение: пусть .

1) AOK и AOC имеют равные высоты, ;

2) CAK и CBK имеют равные высоты, ;

3) ; 4) ;

5) Рассмотрим KBC и секущую AL; A KB, O KC, L BC.

По теореме Менелая .

, ,

x=6 : - верно.

, D<0 – других действительных корней нет.

. Ответ: 21.

З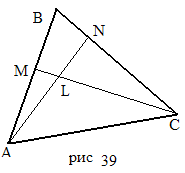 адача 6. На сторонах AB и BC треугольника ABC взяты точки M и N соответственно. Отрезки AN и CM пересекаются в точке L. Площади треугольников AML , CNL и ALC равны соответственно 15, 48 и 40. Найти площадь треугольника ABC.

Решение: ALC и LCN , а также AML и ALC имеют общие высоты, опущенные соответственно на стороны AN и MC. Отсюда следует, что площади этих треугольников относятся как соответствующие основания.

Рассмотрим BMC и секущую AN.

По теореме Менелая (1)

Рассмотрим ABN и секущую MC.

По теореме Менелая (2)

Вычитая из (2) соотношение (1) , получим

Так как то откуда 3AM=MB, а значит, AM= MB= Отсюда следует, что S составляет часть площади треугольника ABC (они имеют общую высоту, проведенную из вершины С).

Тогда S = 4 S =(15+40) .

Ответ: 220

Задача 7 . На стороне AB треугольника ABC взята точка E, а на стороне BC- точка D так, что DC=1, AE=2. Прямые AD и CE пересекаются в точке O. Найти площадь четырехугольника BDOE, если AB=BC=8, AC=6.

Р ешение: Площадь треугольника ABC найдем по формуле Герона:

p = (8+8+6):2=11, S= =

Треугольники BAD и DAC имеют общую высоту, поэтому их площади относятся как длины оснований, то есть , так как S=S +S .

Аналогично, .

Рассмотрим треугольник BEC и секущую AD. По теореме Менелая ,

, S =

S =S

Ответ:

Дополнительные задачи.

1. Отрезок АВ делится точкой D отношении 3:2, а отрезок ВС – точкой Е в отношении 1:3. Отрезки АЕ и CD пересекаются в точке F. Чему равно отношение площадей треугольников ADF и CFE?

2. Площадь треугольника АВС равна 28, точка D лежит на стороне АВ втрое ближе к А, чем к В, а точка Е на стороне ВС втрое ближе к С, чем к В. Прямые CD и АЕ пересекаются в точке F. Чему равны площади треугольника ADF и четырехугольника DBEF?

3. На стороне АВ треугольника АВС взята точка D, а на стороне АС – точка Е так, что АЕ= BD=2. Прямые CD и BE пересекаются в точке О. Найти площадь треугольника ВОС, если АВ=ВС=5, АС=6.

4. На стороне ВС треугольника АВС взята точка D, а на стороне АС – точка Е так, что BD=2, а АЕ=3. Прямые AD и ВЕ пересекаются в точке О. Найти площадь четырехугольника CDOE, если АС=ВС=9, АВ=8.

5. На стороне АС треугольника АВС взята точка D, а на стороне ВС – точка F так, что AD=3, a BF=1. Прямые BD и AF пересекаются в точке О. Найти площадь треугольника АОВ, если АВ=АС=5, ВС=6.

6. На сторонах KL и LM треугольника KLM взяты точки А и В соответственно. Отрезки АМ и ВK пересекаются в точке С. Площади треугольников АСK, BCM и CKM равны соответственно 2, 12 и 8. Найти площадь треугольника LAC.

7. На сторонах FG и GH треугольника FGH взяты точки K и L соответственно. Отрезки KH и FL пересекаются в точке М. Площади треугольников KMF, HML и FMH равны соответственно 2, 4 и 4. Найти площадь треугольника GKL.

8. На сторонах RT и TS треугольника RTS взяты точки А и В соответственно. Отрезки AS и BR пересекаются в точке С. Площади треугольников ACR, BCS и RCS равны соответственно 5, 8 и 10. Найти площадь четырехугольника TACB.

Занятия 9-10. Тема: Комбинированные задачи.

Э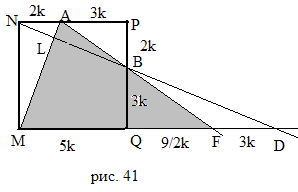 ти занятия посвящены более сложным задачам, которые встречаются на олимпиадах разных уровней. Так как большая часть олимпиадных задач затрагивает небольшое число разделов математики, то школьникам, стремящимся к успеху, полезно знать темы этих разделов и видеть, что многие новые задачи часто не более чем малоузнаваемые вариации прежних.

Задача 1. На стороне NP квадрата MNPQ взята точка A, а на стороне PQ – точка B так, что NA:AP = PB:BQ = 2:3. Точка L является точкой пересечения отрезков MA и NB. В каком отношении точка L делит отрезок MA?

Решение: проведем прямую AB, пусть она пересекает прямую MQ в точке F и пусть прямая NB пересекает прямую MQ в точке D (рис.41).

APB ~ FQB, тогда , откуда QF= .

NPB ~ DQB, тогда , откуда QD = .

FD = QD – QF= .

Из треугольника APB (прямоугольного) по теореме Пифагора AB = k.

Из треугольника QBF (прямоугольного) по теореме Пифагора BF = . Из треугольника AFM по теореме Менелая

, , , .

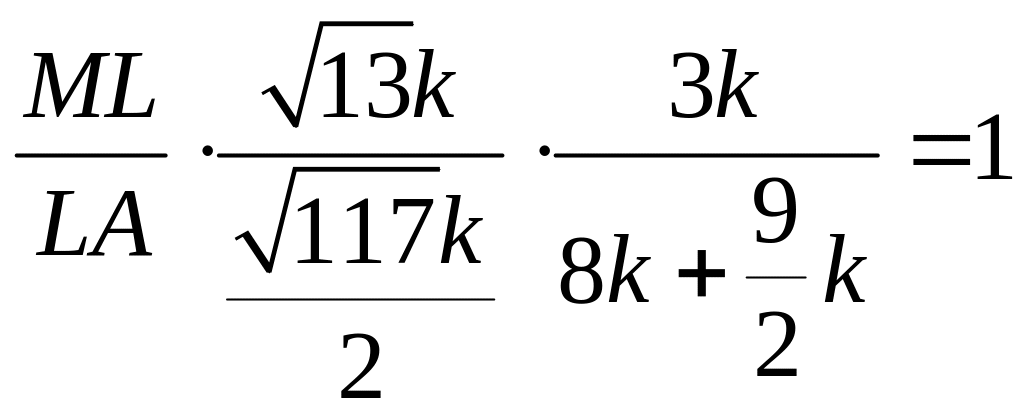Ответ: 25: 4.

Задача 2. Дан параллелограмм ABCD. Точка M делит отрезок AD в отношении p , а точка N делит отрезок DC в отношении q. Прямые BM и AN пересекаются в точке S. Вычислите отношение AS:SN.

Р ешение: если MD=b, то AM=pb; если NC = a, то DN = aq.

Пусть B - точка пересечения прямых BM и CD.

MB D ~ BB C, тогда ;

;

1+p = ; x = .

Прямая BB пересекает две стороны и продолжение третьей треугольника AND. По теореме Менелая

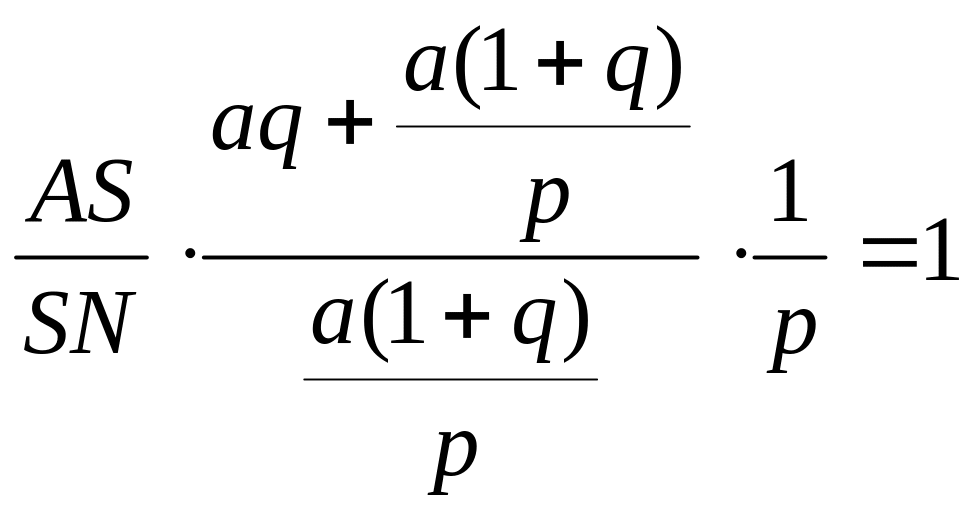, , откуда .

Ответ: .

Задача 3. На сторонах AС и BC взяты точки М и L так, что AM:MC=4:1, CL:LB=3:1. Отрезки AL и BM пересекаются в точке Q. .

1 ) Найти ; 2) На АВ взяли точку N так, что CN – медиана ; , . Найти .

Решение:

1) а) Рассмотрим , BM – секущая (рис.43),

по теореме Менелая ,

б) и имеют равные высоты . Так как ,

в) и имеют равные высоты

2 ) CN-медиана AN=NB. Найдем (рис. 44).

а) , ;

б) ( имеют равные высоты),

; .

в) Рассмотрим ABM и секущую NC.

По теореме Менелая ,

, ,

,

.

Ответ: 11 кв.ед.

Задача 4. На стороне AB ABC взята точка D, а на стороне AC – точка Е так, что длина AE=BD=2. Прямые . Найти , если AB=BC=5, AC=6.

Решение: 1) , ,

2) Рассмотрим ABE, DC – секущая; D AB, O BE, C AE(рис.45).

По теореме Менелая , ; .

Значит, CO – медиана BCE, .

Из ABC по теореме косинусов

,

; .

Ответ: 4.

Примечание 9: если на момент решения задачи теорема косинусов учащимся еще не известна, задачу 4 следует отложить до изучения теоремы.

Задача 5. На сторонах АВ, ВС и СА треугольника АВС отмечены точки и соответственно так, что отрезки и пересекаются в одной точке Q, расположенной внутри треугольника АВС. Пусть Р – точка пересечения отрезков и . Доказать, что .

Доказательство. Эта задача может быть решена многими способами, мы разберем решение, использующее теоремы Менелая и Чевы, чрезвычайно полезные для решения задач такого типа.

Е сли 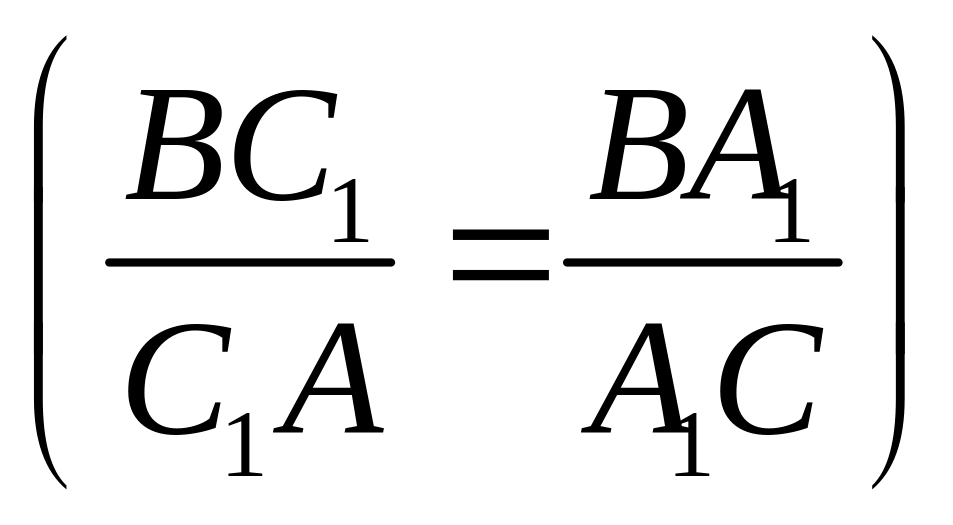, то утверждение задачи может быть доказано достаточно легко. Рассмотрим случай, когда прямые и пересекаются в точке

М ( рис.46). По теореме Менелая для треугольников и имеем:

, , откуда ,

.

Складывая эти равенства, получаем (1)

По теореме Менелая для треугольников и имеем:

,

Учитывая, что , , и складывая уравнения, получаем:

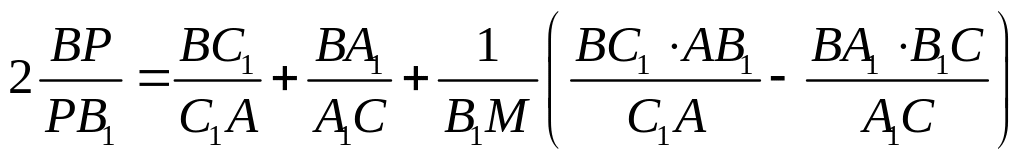. Из теоремы Чевы для треугольника АВС следует, что .

Поэтому (2)

Сравнивая (1) и (2) , получаем требуемое.

З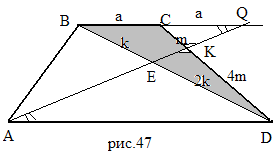 адача 6. В трапеции ABCD с основаниями AD и BC через точку A проведена прямая, которая пересекает диагональ BD в точке E и боковую сторону CD в точке K, причем BE:ED=1:2, CK:KD=1:4. Найдите отношение длин оснований трапеции.

Решение. Пусть BC=a, AD=b. Необходимо найти . Пусть BC AK=Q (рис.47).

1) По теореме Менелая для BCD и секущей AQ имеем CQ=a , BC=CQ=a.

2) CKQ ~ DKA по двум углам, тогда Так как а = BC, b=AD, то

Ответ:

Дополнительные задачи.

1. Высота трапеции ABCD равна 7, а длины оснований AD и BC равны соответственно 8 и 6. Через точку E, лежащую на стороне CD, проведена прямая BE, которая делит диагональ AC в точке O в отношении AO:OC=3:2. Найдите площадь треугольника OEC.

2. Через середину M стороны BC параллелограмма ABCD, площадь которого 1, и вершину A проведена прямая, пересекающая диагональ BD в точке Q. Найдите площадь четырехугольника QMCD.

3. В треугольнике ABC точки K и L принадлежат соответственно сторонам AB и BC. AK:BK=1:2, CL:BL=2:1. Q- точка пересечения отрезков AL и CK. S =1.

Найдите площадь треугольника ABC.