9.3. Выявление роли факторов динамики, структуры и взаиморасположения

явлений индексным методом

В рассмотренном ранее примере взаимосвязи общих индексов стоимостного объёма, цен и физического объёма имеет место соотношение

значение которого состоит в том, что на его основе выделяется влияние отдельных факторов (цены и физического объёма) на изменение стоимостного объёма товаров. Так, если общий уровень цен на товары в отчётном периоде вырос на 11,6% по сравнению с базисным периодом ( а физический объём товаров вырос в отчётном периоде на 7,5% по сравнению с базисным периодом ( то индекс стоимостного объёма товаров равен

.

Т.е. стоимостной объём товаров вырос в отчётном периоде на 20% по сравнению с базисным периодом, что было обусловлено двумя факторами: а) ростом цен в среднем на 11,6%; б) увеличением физического объёма товаров на 7,5%.

При изучении динамики качественных показателей большое значение имеет определение изменения средней величины индексируемого показателя, которое обусловлено двумя факторами - изменением значений индексируемого показателя у отдельных групп единиц и изменением структуры совокупности.

Например, из формулы средней цены

следует, что на её изменение оказывает влияние как изменение цен на отдельные товары , так и изменение числа отдельных товаров в рассматриваемой совокупности.

Для анализа изменения качественных показателей с помощью средних величин (таких как средняя цена , средняя себестоимость единицы изделия , средняя выработка работника , средняя заработная плата работника , средняя трудоёмкость изделия и др.) в статистической практике применяются индексы средних величин, которые зависят от соответствующих индексов уровня и индексов структурных сдвигов. В общем виде эта зависимость следующая

где

называется индексом переменного состава показателя (индексом среднего уровня), так как в качестве весов – соизмерителей в нём выступают составы текущего и базисного периодов;

называется индексом постоянного состава показателя (индексом уровня или индексом фиксированного состава), так как в качестве весов-соизмерителей в нём выступает состав текущего периода ;

называется индексом структурных сдвигов (индексом структуры), так как в нём изменяются лишь веса-соизмерители состава и .

Рассмотрим пример. По известным индексам уровня цен и структурных сдвигов необходимо определить, как изменилась средняя цена и за счёт действия каких факторов произошло это изменение.

Для ответа на этот вопрос надо рассматривать данные о структуре товара, т.е. рассматривать составляющие индекса средней цены

Таким образом, средняя цена товаров снизилась на 3,1%. Это произошло за счёт изменения структуры (состава) товаров на 5%, хотя цены на товары постоянного состава возросли в текущем периоде на 2%.

Для анализа соотношения явлений на различных территориях (взаиморасположения) используются общие территориальные индексы. Например, при изучении соотношения уровня цен на товары в различных городах (странах) исчисляют территориальные индексы цен

В этом случае общие (сводные) индексы характеризуют соотношение цен в городе А (стране А) по сравнению с городом Б (страной Б в единой валюте). Числитель индекса характеризует фактический стоимостной объём данного ассортимента товаров в городе А (стране А). Знаменатель индекса отражает условную величину стоимостного объёма (в единой валюте) данного ассортимента товаров в городе Б (стране Б).

Соответствующий территориальный индекс физического объёма товаров определяют по формуле

Территориальный индекс стоимостного объёма товаров можно представит в виде

Последнее равенство выражает взаимосвязь между территориальными индексами стоимостного объёма, цен и физического объёма товаров.

Тест 3

В качестве варианта ответа необходимо выбрать вариант, содержащий наиболее полный, правильный и точный ответ на вопрос.

№	Вопрос	Варианты ответа
1	Рядом динамики называется	1) совокупность показателей динамики, расположенных в определенной последовательности 2) расположенные в хронологическом порядке показатели, отображающие развитие явления во времени 3) зависимость статистических показателей от времени 4) хронологическое описание явлений и процессов
2	Интервальные ряды отображают	1) уровни ряда на дату 2) результаты развития показателей с учетом предшествующих периодов 3) итоги развития явлений за отдельные периоды времени 4) интервальные показатели
3	Уровень ряда динамики - это	1) определенное значение варьирующего признака в совокупности 2) теоретическое значение показателя, изменяющегося во времени 3) значение показателя времени в моментном или интервальном ряду 4) величина показателя на определенную дату или за определенный период времени
4	Если все уровни ряда динамики сравниваются с одним и тем же уровнем, показатели называются	1) цепными 2) соотнесёнными 3) базисными 4) абсолютными
5	Если сравниваются смежные уровни ряда динамики, показатели называются	1) цепными 2) соотнесёнными 3) базисными 4) абсолютными
6	Абсолютный прирост исчисляется как	1) отношение уровней 2) сумма уровней 3) разность уровней 4) отношение темпов роста
7	Темп роста исчисляется как	1) отношение уровней ряда 2) разность уровней ряда 3) отношение цепных приростов 4) сумма уровней ряда
8	Средний уровень интервального ряда определяется как	1) средняя арифметическая 2) средняя гармоническая 3) средняя хронологическая 4) средняя геометрическая
9	Темп прироста можно определить через темп роста в процентах по формуле	1) 2) 3) 4)
10	Какие факторы определяют тенденцию развития?	1) периодические 2) случайные 3) постоянные 4) спорадические
11	Сезонные колебания представляют собой равномерно повторяющиеся изменения ряда динамики	1) через определенные промежутки времени с годичным интервалом 2) внутри года 3) внутри определенного сезона 4) через промежутки времени с месячным интервалом
12	Для выявления тренда используется	1) метод аналитического выравнивания 2) ряд Фурье 3) регрессионный анализ 4) метод укрупнения интервалов
13	Можно ли изучить взаимосвязи социально-экономических явлений по данным рядов динамики?	1) да 2) нет 3) вероятно 4) не знаю
14	Метод аналитического выравнивания состоит в том, что	1) первоначальный ряд динамики преобразуется в ряды более продолжительных периодов 2) по исходным данным определяются теоретические уровни, в которых случайные колебания погашаются 3) основная тенденция ряда динамики рассчитывается как теоретическая функция времени 4) уровни ряда выравниваются при отбрасывании членов, имеющих наибольшие и наименьшие значения уровней
15	Метод наименьших квадратов состоит в том, что	1) минимизируются квадраты уровней ряда динамики 2) сумма квадратов уровней ряда динамики должна быть минимальной 3) сумма квадратов отклонений теоретических значений уровня от эмпирических должна быть минимальной 4) сумма отклонений теоретических значений уровня от эмпирических должна быть равна нулю
16	Для равноускоренного (равнозамедленного) развития присуще изменение уровней ряда	1) с постоянными абсолютными цепными приростами 2) с постоянными цепными темпами прироста 3) с постоянными цепными темпами роста 4) с уменьшающимися по величине цепными приростами
17	Индексами в статистике называют	1) относительные показатели характеризующие степень выполнения плана, динамику, соотношение в пространстве уровней явлений 2) темпы прироста 3) соотношения разноименных показателей, характеризующих уровень развития явления 4) цифры, буквы и символы при статистических показателях
18	Какие индексы бывают по степени охвата изучаемого сложного явления?	1) комплексные 2) симплексные 3) индивидуальные 4) соизмеримые
19	Общие индексы характеризуют	1) динамику общепринятых показателей 2) сводные результаты изменения явления по всем единицам статистической совокупности 3) изменение общей суммы индексируемого показателя по всей совокупности 4) степень выполнения плана по показателю
20	Общие индексы строятся в формах	1) степенных и экспоненциальных 2) индивидуальных и групповых 3) прямых и обратных 4) средних и агрегатных
21	Общий индекс цен с весами текущего периода называется индексом	1) Фишера 2) Пааше 3) Ласпейреса 4) Доу-Джонса
22	Выбор формы общего индекса зависит от	1) характера исходных данных 2) предпочтения исследователя 3) установок статистических органов 4) случайных факторов
23	Индекс переменного состава цен характеризует	1) соотношение индивидуальных цен отчетного и базисного периодов 2) соотношение цен в среднем 3) соотношение средних цен отчетного и базисного периодов 4) ценовую политику на рынке товаров

Решение задач

Задача 7. Динамика физического объёма производства по часовому заводу характеризуется следующими данными:

Год	1999	2000	2001	2002	2003
Производство часов, тыс. шт.	180	186	180	188	192

Определите:

1) аналитические показатели ряда динамики:

- абсолютные приросты, темпы роста и прироста по годам и к 1999 году;

- абсолютное содержание 1% прироста;

2) средний годовой объём производства часов;

3) среднегодовой абсолютный прирост, среднегодовые темпы роста и прироста.

Проанализируйте рассчитанные показатели и сделайте выводы.

Решение.

1) Расчеты аналитических показателей ряда динамики можно представить в таблице:

Год ( )	1999 (1)	2000 (2)	2001 (3)	2002 (4)	2003 (5)
Производство часов, тыс.шт. ( )	180	186	180	188	192
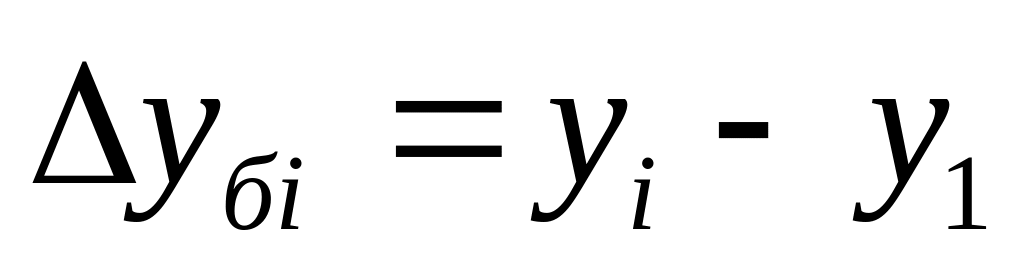, тыс. шт.	-	6	0	8	12
, тыс.шт.	-	6	- 6	8	4
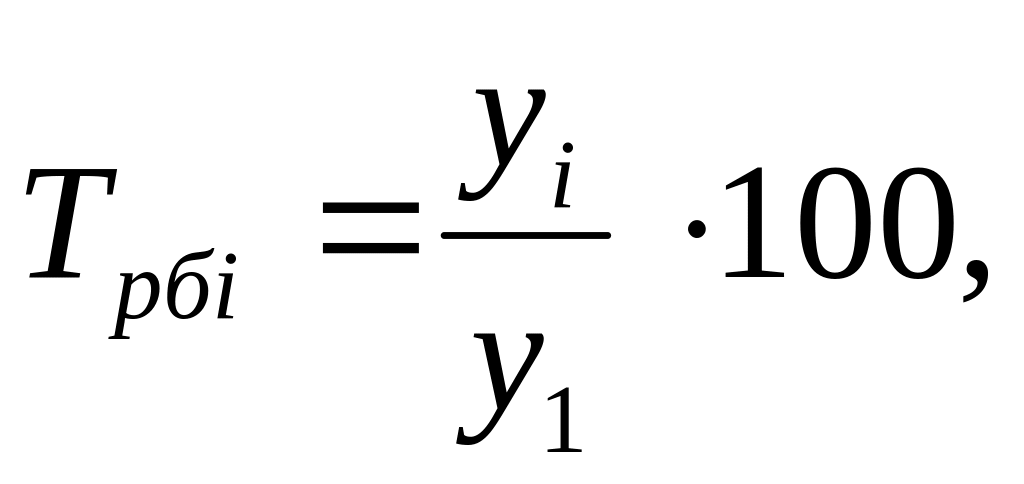%	-	103,3	100	104,4	106,7
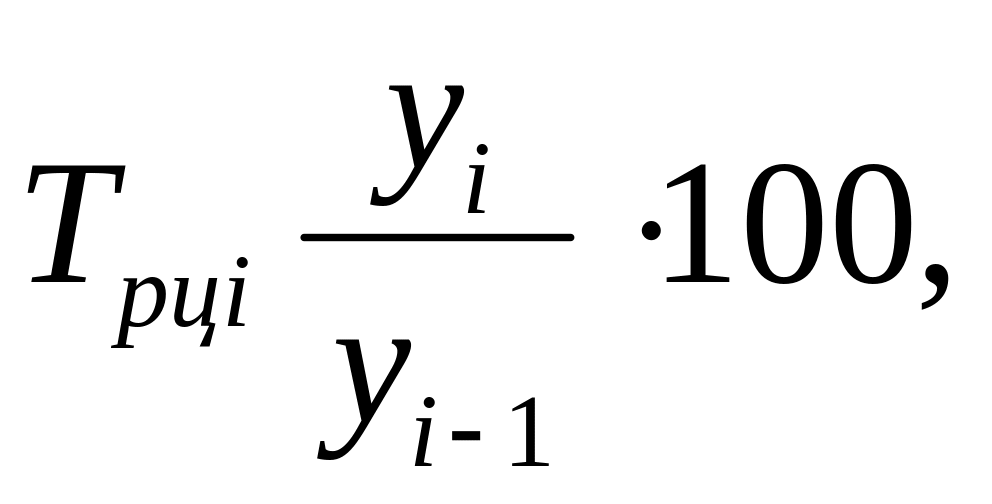%	-	103,3	96,8	104,4	102,1
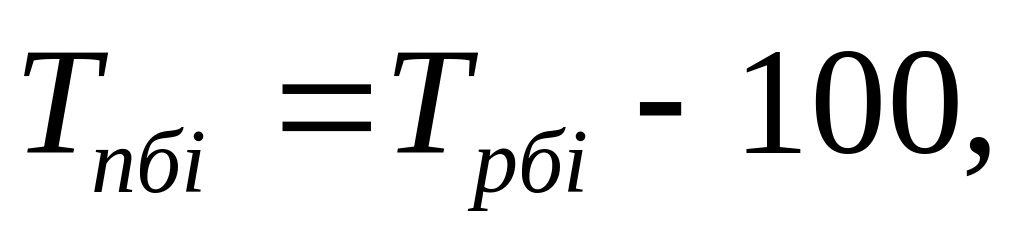%	-	3,3	0	4,4	6,7
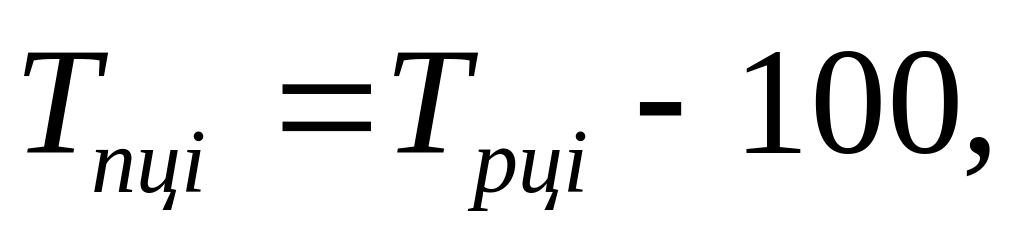%	-	3,3	- 3,2	4,4	2,1
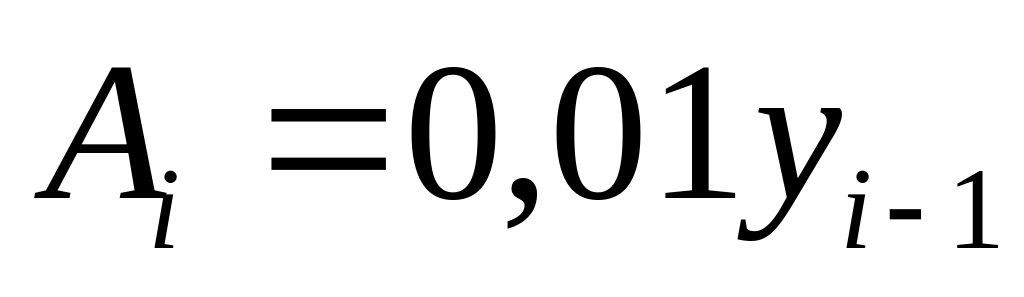, тыс.шт.	-	1,8	1,86	1,8	1,88

2) среднегодовое производство за 1999-2003гг.

тыс.шт.

3) среднегодовые:

- абсолютный прирост

тыс.шт.;

- темп роста

- темп прироста

Выводы: 1. В 2000–2003гг. наблюдался рост производства.

2. В 2001г. наблюдался спад производства часов.

Задача 8. Имеются среднемесячные данные по энергопотреблению промышленных

предприятий города за последние 16 месяцев

Номер месяца	Энергопотребление, млн. кВт	Номер месяца	Энергопотребление, млн. кВт
1	0,25	9	0,42
2	0,34	10	0,46
3	0,22	11	0,65
4	0,36	12	0,51
5	0,21	13	0,53
6	0,45	14	0,65
7	0,55	15	0,81
8	0,65	16	0,67

Провести выявление тренда ряда динамики методом укрупнения интервалов. Сделать вывод.

Решение. Ряд динамики с месячными интервалами преобразуем в ряд динамики с укрупненными интервалами в 4 месяца, причём просуммируем показатели месячных периодов. Результаты укрупнения интервалов приводим в таблице:

Интервал	Энергопотребление, млн. кВт	Интервал	Энергопотребление, млн. кВт
1 – 4 месяцы	0,25+0,34+0,22+0,36=1,17	9 – 12 месяцы	0,42+0,46+0,65+0,51=2,04
5 – 8 месяцы	0,21+0,45+0,55+0,65=1,86	13- 16 месяцы	0,53+0,65+0,81+0,67=2,66

Вывод: По результатам укрупнения интервалов видно, что энергопотребление имеет

отчетливую тенденцию возрастать со временем.

Задача 9. Имеются следующие данные о продаже товаров в трех магазинах:

Магазин	Базисный период		Отчетный период
	цена, тыс. руб.	к-во, шт.	цена, тыс. руб.	к-во, шт.
А	200	1320	214	1501
Б	194	1800	180	1720
В	305	1348	293	1440

Определить: 1) индивидуальные индексы цены, физического объёма и стоимости;

2) групповые индексы цен, физического объёма и товарооборота;

3) общее абсолютное изменение товарооборота по группе и в том числе за счёт изменения уровня цен и физического объема. Сделать выводы.

Решение.

1) Индивидуальные индексы цен, физического объёма и стоимости отдельных товаров определяем по формулам

а результаты расчётов представляем в таблице

Товар
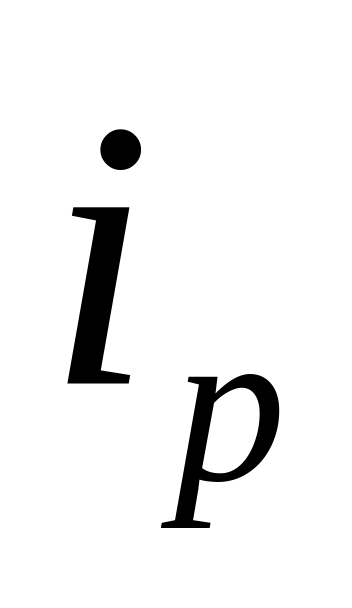
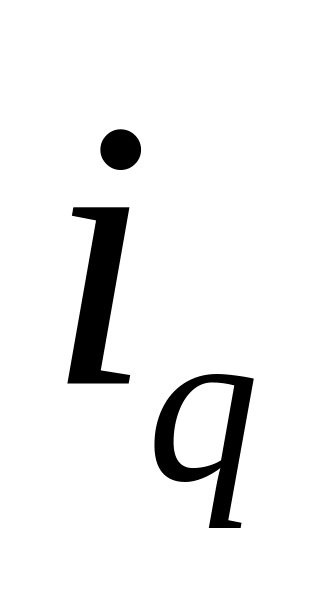
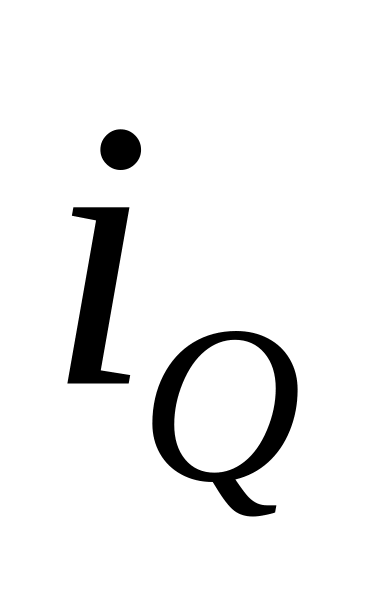
А	1,070	1,137	1,217
Б	0,928	0,956	0,887
В	0,961	1,068	1,026

2) Общие (групповые) индексы:

цен

,

т.е. уровень цен в отчётном периоде по сравнению с базисным снизился на 1,9%;

физического объёма

,

т.е. физический объём товаров в отчётном периоде по сравнению с базисным вырос на 4,8%;

товарооборота

,

т.е. товарооборот в отчётном периоде увеличился на 2,8% по сравнению с базисным периодом.

Поскольку между индексами существует взаимосвязь

то можно сделать вывод: товарооборот вырос на 2,8%, что было обусловлено влиянием двух факторов – снижением уровня цен на 1,9% и увеличением физического объёма на 4,8%.

3) Абсолютные приросты товарооборота рассчитываются, как разность числителя и знаменателя соответствующих индексов. Общий абсолютный прирост равен разности числителя и знаменателя индекса товарооборота

тыс. руб.

в том числе абсолютный прирост за счёт изменения цен

тыс. руб.

и за счёт изменения количества товаров

тыс. руб.

Видно, что общее изменение товарооборота равно сумме изменений за счет влияния отдельных факторов

тыс. руб.

Задача 10. По данным задачи 9 исчислить по трем магазинам: 1) индексы переменного состава цен, постоянного состава цен и структурных сдвигов; 2) определить абсолютный прирост средней цены товаров. Пояснить, под влиянием каких факторов это произошло.

Решение.

1) индекс переменного состава (средней цены)

,

т.е. средняя цена товаров в отчетном периоде снизилась на 1,5%. Индекс постоянного состава (общий индекс цен) рассчитан в предыдущей задаче

Индекс структурных сдвигов (структуры)

Так как между индексами товарооборота, цен и структуры справедлива взаимосвязь

, то можно сделать вывод: средняя цена товаров снизилась на 1,5% за счёт влияния двух факторов – уменьшения уровня цен на 1,9% и изменения количества товаров в сторону увеличения на 0,4%.

2) Общий абсолютный прирост средней цены равен

тыс. руб./шт.,

в том числе за счет изменения уровня цен

тыс. руб./шт.,

и за счёт изменения количества товаров (структуры)

тыс. руб./шт.

Очевидно, что общий абсолютный прирост равен сумме приростов за счет влияния отдельных факторов

тыс. руб./шт.

Задача 11. По имеющимся данным определить общий индекс физического объёма продукции:

Вид продукции	Продукция базисного периода, млн. руб.	Индивидуальные индексы Физического объёма, %
Сапоги мужские	24	150
Костюмы женские	48	90
Куртки детские	32	120

Пояснить полученный результат.

Решение. Общий индекс физического объёма рассчитывается по формуле среднего арифметического индекса со стоимостными весами базисного периода

Физический объём продукции в отчетном периоде вырос на 13,1% по сравнению с базисным периодом.