Центральна симетрія. Означення. Властивості.

Зафіксуємо на площині деяку точку та поставимо у відповідність довільній точці точку , симетричну їй відносно точки (тобто точка є серединою відрізка ). Симетричною до точки вважається ця сама точка. Побудоване перетворення площини називають симетрією відносно точки або центральною симетрією. Точку називають центром симетрії. Позначати перетворення центральної симетрії будемо символом 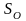. Очевидно, що поворот навколо точки на кут 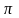є центральною симетрією з центром у даній точці, тобто .

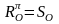Задавати це перетворення можна за допомогою центра симетрії або парою відповідних точок.

Розглянемо деякі властивості даного перетворення. Оскільки центральна симетрія є частинним випадком повороту, то вона володіє всіма перерахованими вище властивостями повороту. Серед властивостей центральної симетрії, не властивих повороту, відмітимо такі:

1) пряма відображається на паралельну до неї пряму, а пряма, яка проходить через центр симетрії, відображається на себе;

2) промінь відображається у паралельний протилежно напрямлений промінь, причому початки цих променів є центрально симетричними точками;

3) відрізок відображається у паралельний, рівний та протилежно напрямлений відрізок;

П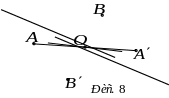 обудова образу прямої при центральній симетрії здійснюється шляхом відшукання образу її довільної точки та проведенні через неї прямої, що паралельна заданій. Можна також будувати пряму, центрально симетричну даній, знайшовши образи двох довільних точок прямої (рис.8).

Побудова образу кола зводиться до відшукання точки, симетричної до його центра, та проведенні кола, радіус якого дорівнює радіусу заданого кола.

Гомотетія та перетворення подібності. Означення.Властивості.

Нехай задане деяке дійсне число , а також на площині зафіксована довільна точка . Кожній точці площини поставимо у відповідність точку таку, що . Оскільки при побудованій таким чином відповідності кожна точка має єдиний образ і різні точки мають різні образи, то введене правило задає перетворення площини. Таке перетворення площини називають гомотетією і позначають символом . Точку називають центром гомотетії, а число - коефіцієнтом гомотетії.

При вектори та напрямлені однаково, тому точки та лежать на промені по одну сторону відносно точки .

П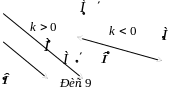 ри вектори та напрямлені протилежно, тому точки та лежать на прямій, яка містить точку , але по різні сторони відносно неї (рис. 9).

При виконується рівність , тому точки та співпадають. Отже, гомотетія з коефіцієнтом є тотожним перетворенням.

При дістаємо, що . Одержана рівність означає, що точки та розташовані симетрично відносно точки . Тому гомотетія з коефіцієнтом є центральною симетрією з центром у точці .

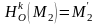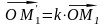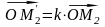Н ехай та Тоді, оскільки та , то , тобто прямі та паралельні. Це дозволяє запропонувати інший спосіб відшукання образу довільної точки, якщо відомий центр гомотетії та пара відповідних гомотетичних точок. Справді, нехай і задана довільна точка . Якщо точка не належить прямій , то образ точки буде знаходитися на перетині прямої та прямої, яка проходить через точку паралельно до прямої (рис. 10).

Якщо ж точка належить прямій , то спочатку знаходять образ довільної точки, яка не належить прямій , а потім за допомогою пари одержаних гомотетичних точок будують образ точки .

Таким чином, гомотетію можна задавати також двома парами відповідних точок, які задовольняють наведені вище обмеження.

Перетворення фігур при гомотетії характеризується рядом властивостей. Зокрема при гомотетії:

1) відстані між точками змінюються в одне і те ж число разів. Рівні відрізки відображаються на рівні відрізки.

Наведемо доведення цієї важливої властивості. Нехай та . Тоді виконуються рівності та . Тому

.

Отже, , що завершує доведення першої частини твердження. Оскільки довжини відрізків, які є образами рівних відрізків, відрізняються від довжин прообразів однаковим множником , то вони рівні.

2) колінеарні вектори відображаються у колінеарні;

3) пряма відображається на пряму, причому паралельні прямі переходять у паралельні прямі;

4) відрізок переходить у відрізок, а точка, яка ділить відрізок у деякому відношенні, переходить у точку, яка ділить образ відрізка у такому ж відношенні. Зокрема середина відрізка переходить у середину відрізка;

5) півплощина переводиться у півплощину;

6) зберігаються величини кутів. Перпендикулярні прямі при гомотетії переходять у перпендикулярні;

7) при гомотетії коло з радіусом переходить у коло з радіусом , центр якого знаходиться у точці, яка є образом центра заданого кола.

Властивість 3) дозволяє описати алгоритм побудови прямої, яка є образом заданої прямої при вибраній гомотетії: спочатку шукають образ довільної точки прямої і через одержану точку проводять пряму паралельно до заданої.

Нехай задані дві різні паралельні прямі та , причому . Тоді існує єдина гомотетія, яка точку переводить у точку , а точку - у точку . Такою є гомотетія з коефіцієнтом та з центром у точці, в якій перетинаються прямі та . Умова того, що задані паралельні прямі – різні, не є обов’язковою.

Побудова кола, гомотетичного до заданого, зводиться до відшукання точки, яка є образом центра кола при вибраній гомотетії та проведенні кола, радіус якого дорівнює радіусу заданого кола, помноженому на .

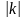Іноді доводиться вибрати гомотетію, яка переводить одне коло у інше. У цьому випадку можна скористатися наступним твердженням.

Теорема. Існує дві гомотетії, кожна із яких переводить деяке коло у довільне неконгруентне коло.

Д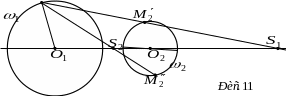 оведення. Нехай задані два кола та з різними центрами у точках та і радіусами та , причому . Виберемо на колі точку та проведемо у колі діаметр, який паралельний прямій . Цей діаметр перетне коло у деяких точках та . Дві гомотетії, кожна з яких визначається двома парами відповідних точок та або згідно з властивістю 6) є шуканими і відображають коло на (рис. 11), оскільки відображають центр кола у центр кола , а точку на колі – у точку на колі . Центр однієї із гомотетій розташований у точці перетину прямих та , а її коефіцієнт при умові, що точки та розташовані по одну сторону відносно прямої , дорівнює . Центр

другої гомотетії розташований у точці перетину прямих та , а її коефіцієнт рівний . Третьої гомотетії, яка відображає коло на нема, оскільки вона перевела б радіус у паралельний радіус кола , тобто у радіус або і співпала б із однією із двох побудованих гомотетій.

Якщо центри кіл співпадають, то коло на відображають дві гомотетії з центром у центрі даних кіл та коефіцієнтами і .

Нехай задано дійсне число .

Перетворення площини, при якому відстані між точками змінюються в одне і те ж число разів, називається перетворенням подібності з коефіцієнтом подібності .

Згідно з означенням, якщо точки та відображаються при перетворенні подібності з коефіцієнтом на точки та , то .

Такі перетворення існують і прикладом може бути гомотетія з довільним коефіцієнтом , при якій, як ми знаємо, відстані між точками змінюються в разів. Позначатимемо перетворення подібності з коефіцієнтом символом . Геометричні фігури, які можна отримати одну з іншої перетворенням подібності, називають подібними.

Перетворення подібності з коефіцієнтом є рухом, оскільки воно не змінює відстані між точками. Тому рухи є частинним випадком перетворень подібності.