
- •Паралельне перенесення. Означення. Властивості.
- •Осьова симетрія. Означення. Властивості. Способи задання.
- •5) Коло перетворюється у рівне коло.
- •Поворот. Означення. Властивості.
- •При повороті:
- •5) Коло перетворюється у рівне коло.
- •Центральна симетрія. Означення. Властивості.
- •Гомотетія та перетворення подібності. Означення.Властивості.
Паралельне перенесення. Означення. Властивості.
Нехай заданий
вектор
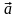 ,
паралельний до деякої площини. Довільній
точці
,
паралельний до деякої площини. Довільній
точці
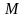 цієї площини поставимо у відповідність
точку
цієї площини поставимо у відповідність
точку
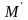 таку, що
таку, що
 .
Одержане перетворення, яке ми будемо
позначати символом
.
Одержане перетворення, яке ми будемо
позначати символом
 ,
називається паралельним
перенесенням
на вектор
.
,
називається паралельним
перенесенням
на вектор
.
К рім
вектора, паралельне перенесення можна
задавати парою відповідних точок.
Побудова образу точки
при паралельному перенесенні циркулем
та лінійкою реалізується у два етапи:
спочатку через задану точку проводять
пряму паралельно до вибраного вектора,
а потім від цієї точки відкладають
відрізок, довжина якого дорівнює довжині
вектора паралельного переносу. Точка
така, що
,
є шуканим образом точки
(рис. 1).
рім
вектора, паралельне перенесення можна
задавати парою відповідних точок.
Побудова образу точки
при паралельному перенесенні циркулем
та лінійкою реалізується у два етапи:
спочатку через задану точку проводять
пряму паралельно до вибраного вектора,
а потім від цієї точки відкладають
відрізок, довжина якого дорівнює довжині
вектора паралельного переносу. Точка
така, що
,
є шуканим образом точки
(рис. 1).
Перерахуємо деякі властивості даного перетворення. При паралельному перенесенні:
1) зберігаються відстані між точками, тобто дане перетворення є рухом (переміщенням),
2) пряма відображається на паралельну до неї пряму, а у випадку, коли вектор перенесення паралельний до прямої, відображається на себе. Паралельні прямі переходять у паралельні, причому відстані між парами цих паралельних прямих рівні;
3) відрізок переходить у паралельний та рівний відрізок, а точка, що ділить відрізок у деякому відношенні, переходить у точку, яка ділить образ відрізка у такому ж відношенні. Зокрема, точка, яка є серединою відрізка переходить у точку, яка є серединою відрізка;
4) кути переходять у рівні і так само орієнтовані кути, зокрема перпендикулярні прямі переходять у перпендикулярні;
5) коло перетворюється у рівне коло.
Побудова образу прямої при паралельному перенесенні здійснюється шляхом відшукання образу її довільної точки та проведенні через неї прямої, що паралельна заданій. Якщо вектор перенесення паралельний до прямої, то вона відображається на себе.
Побудова образу кола зводиться до відшукання образу його центра та проведенні кола, радіус якого дорівнює радіусу заданого кола.
Осьова симетрія. Означення. Властивості. Способи задання.
Нехай на площині
задана деяка пряма
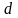 .
Кожній точці
площини поставимо у відповідність
симетричну їй відносно прямої
точку
(рис. 2).
.
Кожній точці
площини поставимо у відповідність
симетричну їй відносно прямої
точку
(рис. 2).
М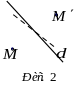 и
називаємо дві точки симетричними
відносно деякої
прямої,
якщо відрізок, який їх сполучає,
перпендикулярний до даної прямої та
ділиться нею пополам. Симетричними до
точок на прямій вважаються ці самі
точки. Побудоване таким чином відображення
є перетворенням площини. Його називають
симетрією
відносно прямої
або осьовою
симетрією.
Пряму
при цьому називають віссю симетрії.
Розглянуте перетворення дальше будемо
позначати символом
и
називаємо дві точки симетричними
відносно деякої
прямої,
якщо відрізок, який їх сполучає,
перпендикулярний до даної прямої та
ділиться нею пополам. Симетричними до
точок на прямій вважаються ці самі
точки. Побудоване таким чином відображення
є перетворенням площини. Його називають
симетрією
відносно прямої
або осьовою
симетрією.
Пряму
при цьому називають віссю симетрії.
Розглянуте перетворення дальше будемо
позначати символом
 .
.
Задавати дане перетворення можна за допомогою осі симетрії або парою відповідних точок, які не співпадають.
П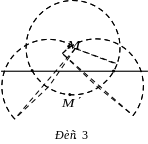 обудову
образу точки
при осьовій симетрії циркулем та лінійкою
можна здійснити наступним чином: спочатку
через вибрану точку проводять пряму
перпендикулярно до осі симетрії та
знаходять точку
обудову
образу точки
при осьовій симетрії циркулем та лінійкою
можна здійснити наступним чином: спочатку
через вибрану точку проводять пряму
перпендикулярно до осі симетрії та
знаходять точку
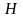 перетину цих двох прямих. Після цього
від точки
на даному перпендикулярі відкладають
відрізок
перетину цих двох прямих. Після цього
від точки
на даному перпендикулярі відкладають
відрізок
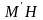 ,
довжина якого дорівнює довжині відрізка
,
довжина якого дорівнює довжині відрізка
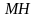 .
Точка
є шуканим образом точки
.
.
Точка
є шуканим образом точки
.
Опишемо деякі властивості осьової симетрії. При даному перетворенні:
1) зберігаються відстані між точками (тобто дане перетворення є рухом);
2) пряма відображається на пряму, а паралельні прямі перетворюються у паралельні, причому відстані між парами цих паралельних прямих рівні;
3) відрізок переходить у рівний відрізок, а точка, що ділить відрізок у деякому відношенні, переходить у точку, яка ділить образ відрізка у такому ж відношенні. Зокрема, точка, яка є серединою відрізка переходить у точку, яка є серединою відрізка;
4) кути переходять у рівні, але протилежно орієнтовані кути. Перпендикулярні прямі переходять у перпендикулярні прямі;
