
- •1.Понятие о сапр и перспективы развития сапр/астпп.
- •2.Состав и структурная схема сапр.
- •3.Принципы создания сапр. Достоинства сапр и астпп.
- •4.Особенности построения сапр
- •5.Графические стандарты
- •6.Декомпозиция проектных задач
- •7.Техническое и математическое обеспечение сапр
- •8.Программное обеспечение сапр
- •9.Информационное и организационное обеспечение сапр
- •10.Лингвистическое и методическое обеспечение сапр
- •11.Техническое обеспечение системы AutoCad
- •12.Основные черты сапр
- •13.Типы компьютерных сетей
- •14.Рабочие компьютерные станции и их процессоры.
- •15.Графические дисплеи и электронный командный планшет
- •16. Принтеры и их виды. Плоттеры, сканеры и дигитайзеры.
- •Матричные принтеры
- •Струйные принтеры
- •Лазерные принтеры
- •17. Банк данных и база данных caпp.
- •18.Принципы организации и операции для работы с субд.
- •19. Макросы и их виды.
- •20.Средства двумерного черчения. Элементы чертежа и методы их построения.
- •22.Система координат и способ указания координат точек в AutoCad. Пиктограммы системы координат.
- •23.Команды получения справок системы AutoCad
- •25.Команды редактирования графического редактора системы AutoCad(меню Modify).
- •26. Команда "Слои" (Layers) графического редактора системы AutoCad.
- •27.Блоки(создание, вставка и изменение) в графическом редакторе системы AutoCad
- •28.Объектная привязка в графическом редакторе системы AutoCad
- •29.Проставление размеров в графическом редакторе системы AutoCad (меню Dimension)
- •30.Размерные переменные в графическом редакторе системы AutoCad.
- •31.Представление чертежей на дисплее в графическом редакторе системы AutoCad (меню View).
- •32.Команда отмены сделанных построений (Undo).
- •33.Деление (Divide) и разметка (Measure) объектов в графическом редакторе системы AutoCad.
- •34. Редактирование полилиний (команда Pedit) в графическом редакторе
- •35.Управления трехмерными видами и Перспектива
- •36. Изменение элементов чертежа (команда Change)
- •37. Вспомогательные средства черчения в гр-ом ред-ре AutoCad.
- •38. Построение трехмерных объектов (полилиний, граней, поверхностей) в гр-ком ред-ре системы AutoCad.
- •39. Построение и редактирование трехмерных многоугольных сетей в графическом редакторе системы AutoCad.
- •40. Пользовательские системы координат в графическом редакторе системы AutoCad
- •41. Отображение нескольких окон и два вида пространств в графическом редакторе системы AutoCad.
- •42. Атрибуты блоков в графическом редакторе системы AutoCad.
- •43.Вывод компьютерных чертежей на бумагу в графическом редакторе системы
- •44.Переменные графического редактора системы AutoCad: названия, возможные значения.
- •45.Целевая функция для решения задачи оптимизации параметров гидропневмо подвески автомобиля
- •46.Основы теории гидропневматических упругих элементов подвески.
- •47.Выбор требуемой вертикальной упругой характеристики подвески автомобиля.
- •48.Алгоритм оптимизации методом Нелдера-Мида.
- •49.Симплексный и градиентный методы оптимизации
- •50.Возможности трехмерного моделирования и его виды
- •51.Каркасное моделирование.
- •52.Поверхностное моделирование и применяемые типы поверхностей.
- •53.Моделирование методом конструктивного представления, булевые операции.
- •54. Преимущество твердотельного моделирования и метод граничного представления.
- •55. Программный пакет динамического анализа твердотельных моделей adams. Программный пакет adams: назначение, общая структура, модули и их возможности.
- •56. Программный пакет adams: модуль View (назначение, меню File, Edit, Review)
- •57. Программный пакет adams: модуль View (меню View, Simulate, Settings).
- •58. Программный пакет adams: модуль View (меню Build).
48.Алгоритм оптимизации методом Нелдера-Мида.

Последовательность работы метода Нелдера-Мида:
Задается исходный симплекс (xk, k=1,…,n+1), к – номер вершины симплекса;
Вершины
симплекса упорядочиваются по убыванию
целевой функции
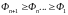 .
.
Определяются координаты геометрического центра фигуры, состоящей из n лучших вершин (не включая
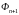 ).
).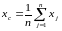
Найденный центр отражается. Координаты точки рассчитываются по формуле:
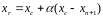 ,
,
 .
.
В точке
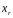 рассчитываем значение целевой функции
рассчитываем значение целевой функции
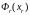 .
.
Значение целевой функции
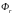 сравнивается с ее значением в вершинах
исходного симплекса. В результате
сравнения возможны следующие варианты:
сравнивается с ее значением в вершинах
исходного симплекса. В результате
сравнения возможны следующие варианты:
Если
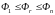 ,
т.е.
-
не лучшая, но и не худшая точка по
сравнению с исходным симплексом. Тогда
вершина с координатой
,
т.е.
-
не лучшая, но и не худшая точка по
сравнению с исходным симплексом. Тогда
вершина с координатой
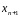 заменяется на вершину с координатой
и
выполняется следующий шаг поиска,
начиная с п.2.
заменяется на вершину с координатой
и
выполняется следующий шаг поиска,
начиная с п.2.Если
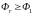 ,
то направление считается удачным и
делается попытка растяжения симплекса
в этом направлении.
,
то направление считается удачным и
делается попытка растяжения симплекса
в этом направлении.
Рассчитывается
координата новой точки:
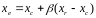
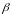 - коэффициент
растяжения,
- коэффициент
растяжения,
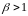 (
(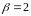 ).
).
В полученной точке
рассчитываем
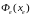 .
Если
.
Если
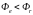 ,
то попытка удачная.
меняем на
,
то попытка удачная.
меняем на
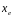 .
.
Если же
 ,
то вершина
меняем
на
и возвращаемся к п.2.
,
то вершина
меняем
на
и возвращаемся к п.2.
Если
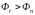 ,
то симплекс признается слишком большим
и выполняется его сжатие.
,
то симплекс признается слишком большим
и выполняется его сжатие.
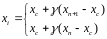

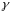 - коэф. сжатия,
- коэф. сжатия,
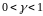 ,
,
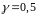 .
.
В этой точке
рассчитывается целевая функция
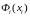 и если
и если
 ,
то сжатие считается удачным и вершина
меняется на
,
то сжатие считается удачным и вершина
меняется на
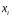 и возвращаемся к п.2.
и возвращаемся к п.2.
Если
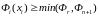 ,
то выполняется текущего симплекса новым
,
то выполняется текущего симплекса новым
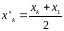
После этого пересчета делается проверка останова задачи:
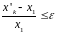 - погрешность
решения.
- погрешность
решения.
Если условие выполняется, то решение останавливается. Если условие не выполняется, то со значениями координат симплекса идем к п.2.
49.Симплексный и градиентный методы оптимизации
Симплексный метод.
Симплекс – многогранник, число сторон которого на одну больше мерности пространства.

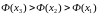
Для поиска новой вершины применяется способ отражения.
Е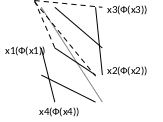 сли
сли
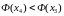 ,
то процесс удачный.
,
то процесс удачный.
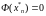
 - оптимальное
значение
- оптимальное
значение
Если
 ,
,
то возвращаемся назад и берем х2.
Градиентный метод.
Упрощенно принцип работы градиентных методов минимизации функций полно представить следующим образом:
1) в исходной точке поиска с координатой х0 определяется направление аитиградиента;
2) вдоль этого направления выполняется шаг заданной длины;
3) в полученной таким образом новой точке опять определяется направление антиградиента и т.д.
Процесс проводится до тех пор, пока происходит улучшение результата, т.е. идет убывание функции F(x).
Отличие разных градиентных методов друг от друга состоит в способе выбора длины и конкретного направления шага на каждом этапе поиска.
Наиболее простым методом является тот, в которой движение вдоль направления антиградиента осуществляется с постоянным шагом:

где
 и
и
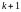 -
номера предыдущей и последующей итерации
поиска.
-
номера предыдущей и последующей итерации
поиска.
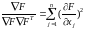 - модуль градиента.
- модуль градиента.
Если значение
целевой функции в новой точке оказывается
больше значения в предыдущей точке,
т.е. Fk+1
> Fk
, то
производится возвращение в предыдущую
точку, потом шаг делится пополам и
процесс продолжается с уменьшенным
шагом. Решение останавливается тогда,
когда величина шага оказывается меньше
некоторого заданного малого числа
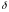 или модуль градиента становится меньше
другого заданного числа
или модуль градиента становится меньше
другого заданного числа
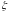 .
.
В некоторых случаях более эффективна является движение с шагом, пропорциональным модулю градиента;
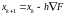
Еще более совершенном градиентным методом является метод наискорейшего спуска, в котором используется одномерный поиск (вдоль одного направления). Его особенность состоит в том, что определив направление антиградиента в исходной точке, определяют точку относительного минимума целевой функции по этому направлению, потом в этой точке снова рассчитывают антиградиент, и процесс повторяется до тех пор, пока последующие итерации позволяют улучшать результат (уменьшать значение целевой функции).
