28.Интегрирование по частям при вычислении определенного интеграла.

Пусть на отрезке [a; b] определены и непрерывны функции u(x) и v(x) вместе со своими производными первого порядка и функция   – интегрируема, тогда на этом отрезке интегрируема функция   и справедливо равенство  .Этой формулой удобно пользоваться в тех случаях, когда нам требуется вычислить интеграл  , причем неопределенный интеграл   мы бы искали интегрированием по частям.

29. Вычисление площадей плоских фигур

ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР  

Пусть функция f (х)  непрерывна на отрезке [a ; b].  Если при этом f (х) ≥ 0 на [a ; b], то  площадь S криволинейной трапеции, ограниченной линиями  ,  выразится с помощью интеграла:     (1)  Если же f (х) ≤ 0 на [a ; b], то −f (х) ≥ 0 на [a ; b].  Поэтому площадь S соответствующей  криволинейной трапеции находится по формуле    или     (2)   Наконец, если линия у = f (х) пересекает ось Ох, то отрезок [a ; b] надо разбить на части, в  пределах которых f (х) не меняет знака, и к каждой части применить ту из формул (1) или (2),  которая ей соответствует.  

30. Несобственный интеграл 1 рода

Определение Предположим, что функция   задана на бесконечном промежутке вида  и интегрируема на любом конечном отрезке   , где   . Таким образом, можно рассмотреть функцию, зависящую от верхнего предела, как от переменной:

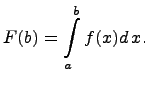Если эта функция имеет предел при   , то число   называется значением несобственного интеграла первого рода:

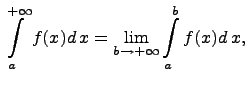а сам определенный интеграл называется сходящимся. Если же предела не существует, то интеграл называется расходящимся и не имеет никакого числового значения..

31. Несобственный интеграл 2 рода

Пусть на полуинтервале   задана функция   , интегрируемая на любом отрезке, принадлежащем данному интервалу, однако не интегрируемая на отрезке   . В точке   эта функция может быть вовсе не определена и стремиться к   , либо вовсе не иметь никакого предела. Рассмотрим функцию

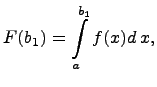
она определена при   . Эта функция может иметь предел при  (левосторонний предел). Этот предел будем называть значением интеграла от   по всему полуинтервалу   и обозначать в точности: 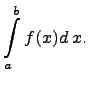Определение. Пусть функция   удовлетворяет указанным выше условиям на   . Несобственным интегралом второго рода назовём определенный интеграл 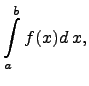значение которого равняется левостороннему пределу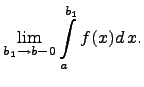

Если этот предел существует, то несобственный интеграл называется сходящимся, а если предела не существует, то расходящимся. Расходящемуся интегралу не приписывается никакого числового значения.

32. Геометрческие приложения определенного интеграла

Площадь фигуры, ограниченной кривыми y=f₁(x) и y=f₂(x), [f₁(x)≤f₂(x)] и прямыми х=а и х=b, находится по формуле       Пример. Вычислить площадь фигуры, ограниченной заданными линиями y=–x², y=–x–2.  Решение. Сделаем чертеж. Найдем абсциссы точек пересечения данных линий: –x²=–x–2 или x²–x–2=0, x₁=–1,x₂=2. Значит,               =–3+1,5+4+2=4,5. Объем тела, полученного вращением криволинейной трапеции вокруг оси Ох; находится по формуле:  .     Длина кривой, заданной уравнением y=f(x), a ≤x≤b,выражается следующим о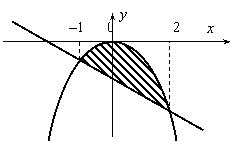 бразом: