22. Интегрировонае простейших иррациональных функция

Рассмотрим интеграл вида  , где подынтегральная функция R рациональна относительно всех ее радикалов. Пусть n - наименьшее общее кратное показателей k_i. Тогда заменой   данный интеграл сводится к интегралу от рациональной функции. Пример. Найти  . Положим  . Тогда .  Интегралы вида    вычисляются при помощи замены  . Пример. Найти 

Положим . Тогда

.

23. Задача о вычислении площади криволинейной трапеции

 Разделим [a, b] точками a = x₀ < x₁ < x₂ < ... < x_n-1 < x_n = b и пусть λ = max(x_k+1 - x_k). Прямые x = x_k разбивают нашу трапецию на n узких полос. Так как функция f(x) непрерывна, то она мало меняется при x_k ≤ x ≤ x_k+1 и без большой погрешности ее можно считать на промежутке [x_k, x_k+1] постоянной и равной f(ξ_k), где ξ_k есть произвольно взятая точка промежутка [x_k, x_k+1]. Легко видеть, что сделанное допущение равносильно тому, что мы принимаем вышеупомянутые полосы за прямоугольники, а всю нашу трапецию - за ступенчатую фигуру, изображенную на рис. 4.

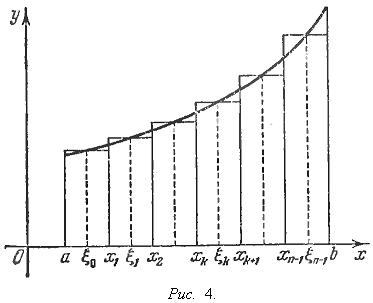
     Площадь этой ступенчатой фигуры, очевидно, равна

     Естественно считать, что эта площадь при малом λ является приближенным значением интересующей нас площади F. Поэтому по определению будем называть площадью нашей криволинейной трапеции предел

     (3)

причем, однако, здесь подлежит доказательству существование этого предела (в предыдущих двух случаях существование этого предела считали очевидным, т. к. масса m и путь s - это заведомо существующие физические величины).

     Сравнивая выражения (1), (2) и (3), полученные в процессе решения рассмотренных задач, замечаем, что с чисто аналитической точки зрения все эти выражения совершенно одинаковы. Поэтому займемся изучением этих выражений, называемых определенными интегралами, уже не интересуясь их конкретным истолкованием

24. Понятие интегральной суммы. Определенный интеграл

Пусть на отрезке [a,b] задана функция y = f(x). Разобьём отрезок [a,b] произвольным образом на n частей точками [x₀ , x₁], [x₁ , x₂], …, [x_i-1 ,x_i], …, [x_n-1 , x_n]; длину i-го отрезка обозначим  :   ; максимальную из длин отрезков обозначим  . На каждом из отрезков [x_i-1 , x_i] выберем произвольную точку   и составим сумму  .  Сумма   называется интегральной суммой. Если существует (конечный) предел последовательности интегральных сумм   при  , не зависящий ни от способа разбиения отрезка [a,b]на части [x_i-1 , x_i], ни от выбора точек  , то функция f(x) называется интегрируемой по отрезку [a,b], а этот предел называется определённым интегралом от функции f(x) по отрезку [a,b] и обозначается  .  Функция f(x), как и в случае неопределённого интеграла, называется подынтегральной, числа a и b - соответственно, нижним и верхним пределами интегрирования.  Кратко определение иногда записывают так:  .  В этом определении предполагается, что b> a. Для других случаев примем, тоже по определению:  Если b=a, то  ; если b<a, то  .