18. Универсальная тригонометрическая подстановка
Рассмотрим
интегрирование выражений полностью
зависящих от тригонометрических
функций, над которыми выполняются лишь
арифметические операции. Такие выражения
называются рациональными функциями
от тригонометрических функций и в
данном случае обозначаются 
.
Например,
, 
, 
.
В
то же время функция 
рациональной
не является.
Теорема. Интеграл
вида 
с
помощью подстановки 
преобразуется
в интеграл от рациональной дроби.
Для
доказательства выразим 
, 
и 
через 
:
;
;
.
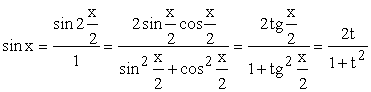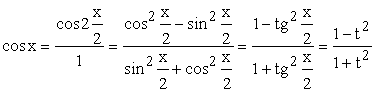19. Интегрирование тригонометрических функций вида Sin ax*Cosbx
Интегралы
вида
находятся с помощью тригонометрических формул
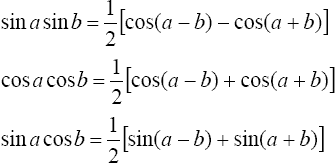
В
результате проведенных
преобразований
,
и
превратились
в рациональные дроби от
.
Подставляя их в исходный интеграл,
получаем:
.
В
данном выражении рациональные дроби
подставлены в рациональную функцию.
Так как над ними выполняются лишь
арифметические операции, то в результате
получается также рациональная дробь.
Итак, рациональную функцию от
тригонометрических функций можно
проинтегрировать, превратив ее в
рациональную дробь.
Подстановка
, 
, 
, 
называется
универсальной тригонометрической
подстановкой.
20. Интегрирование тригонометрических функций вида
В частных случаях один из показателей (m или n) может равняться нулю.
При интегрировании таких функций используется то, что чётную степень косинуса можно выразить через синус, а дифференциал синуса равен cos x dx (или чётную степень синуса можно выразить через косинус, а дифференциал косинуса равен – sin x dx).
Следует различать два случая: 1) хотя бы один из показателей m и n нечётный; 2) оба показателя чётные.
Пусть имеет место первый случай, а именно показатель n = 2k + 1 – нечётный. Тогда, учитывая, что
получим
Подынтегральное выражение представлено в таком виде, что одна его часть – функция только синуса, а другая – дифференциал синуса. Теперь с помощью замены переменной t = sin x решение сводится к интегрированию многочлена относительно t . Если же только степень m нечётна, то поступают аналогично, выделяя множитель sin x, выражая остальную часть подынтегральной функции через cos x и полагая t = cos x.
Если же оба показателя m и n – чётные, то, используя тригонометрические формулы
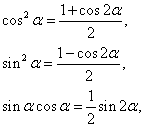
понижают показатели степени синуса и косинуса, после чего получится интеграл того же типа, что и выше. Поэтому интегрирование следует продолжать по той же схеме.
21. Интегрирование иррациональных функций с помощью тригонометрических подстановок
Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.
Интеграл
вида 
.
Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.
Интегралы
этого вида вычисляются с помощью
подстановки 
.
Эта подстановка позволяет преобразовать
тригонометрическую функцию в
рациональную.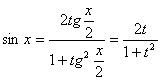
, 
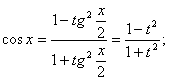Тогда 
Таким
образом: 
Описанное выше преобразование
называется универсальной
тригонометрической подстановкой.