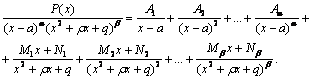- •1. Функция нескольких переменных
- •2. Частное и полное приращение
- •4. Частные производные Функции 2-х переменных
- •5. Полный дифференциал функции. Функции 2-х переменных
- •6. Частные производные высших порядков. Функции двух переменных
- •7. Градиент функции трех переменных
- •8. Производная функции направления
- •9. Экстремум функции двух переменных. Необходимое и достаточное условие экстремума
- •10. Определение первообразной. Теорема о множестве всех первообразных
- •11. Неопределенный интеграл и его свойства
- •12. Метод непосредственного интегрирования
- •13. Метод замены переменной
- •14. Интегрирование по частям
- •15. Простейшие рациональные дроби и их интегрирование
- •16. Разложение правильной дроби на простейшие
- •17. Интегрирование рациональных дробей
- •18. Универсальная тригонометрическая подстановка
- •19. Интегрирование тригонометрических функций вида Sin ax*Cosbx
- •20. Интегрирование тригонометрических функций вида
- •21. Интегрирование иррациональных функций с помощью тригонометрических подстановок
- •22. Интегрировонае простейших иррациональных функция
- •Положим . Тогда
- •23. Задача о вычислении площади криволинейной трапеции
- •24. Понятие интегральной суммы. Определенный интеграл
- •25. Свойство определенного интеграла
- •26. Методы вычисления определенного интеграла. Формула Ньютона – Лейбница
- •27. Замена переменной в определенном интеграле.
- •28.Интегрирование по частям при вычислении определенного интеграла.
- •29. Вычисление площадей плоских фигур
- •30. Несобственный интеграл 1 рода
- •31. Несобственный интеграл 2 рода
- •32. Геометрческие приложения определенного интеграла
- •33. Приближенное вычисление определенных интегралов
- •34. Определение двойного интеграла. Свойства двойного интеграла
- •36. Комплексная плоскость. Арифметические действия над комплексными числами
- •37. Тригонометрические и показательные формы комплексного числа
- •Показательная форма комплексного числа
- •Если обозначить комплексное число , у которого , а , через , то есть , то из (1.3) получимпоказательную форму записи комплексного числа:
- •39. Неполные дифференциальные уравнения и методы их решения.
- •40 Дифференциальные уравнения с разделяющимися переменными
- •41 Однородные дифференциальные уравнения
- •42 Линейные дифференциальные уравнения первого порядка с правой частью
- •43. Однородные дифференциальные уравнения второго порядка
- •44. Дифференциальные уравнения второго порядка с правой частью
- •45. Числовые ряды . Основные понятия. Сходимость ряда. Необходимый признак сходимости
- •46. Гармоничный ряд. Ряд арифметической прогрессии.
- •47. Ряды с положительными членами. Признаки сходимости
- •48. Ряды с членами произвольного знака. Признаки сходимости
- •49. Функциональные ряды. Основные понятия. Область сходимости
- •50. Степенной ряд. Признак сходимости. Область сходимости
- •51. Ряд маклорна и разложение функций в этот ряд
- •52. Ряд Тейлора и разложение функции в этот ряд
- •53. Приминение рядов для вычисления определенных интегралов
13. Метод замены переменной
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть
требуется вычислить интеграл ![]() Сделаем
подстановку
Сделаем
подстановку ![]() где
где ![]() —
функция, имеющая непрерывную производную.
—
функция, имеющая непрерывную производную.
Тогда ![]() и
на основании свойства инвариантности
формулы
интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой:
и
на основании свойства инвариантности
формулы
интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой:
![]()
14. Интегрирование по частям
Интегрирование
по частям — применение следующей
формулы для интегрирования:
![]() Или:
Или:
![]() В частности, с помощью n-кратного
применения этой формулы находится
интеграл
В частности, с помощью n-кратного
применения этой формулы находится
интеграл
![]() где
где ![]() —
многочлен
—
многочлен ![]() -ой
степени.
-ой
степени.
15. Простейшие рациональные дроби и их интегрирование
Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.
Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.
Всякую
правильную рациональную дробь ![]() ,
знаменатель которой разложен на
множители
,
знаменатель которой разложен на
множители![]()
можно
представить (и притом единственным
образом) в виде следующей суммы простейших
дробей:
![]()
где ![]() —
некоторые действительные коэффициенты,
обычно вычисляемые с помощью метода
неопределённых коэффициентов.
—
некоторые действительные коэффициенты,
обычно вычисляемые с помощью метода
неопределённых коэффициентов.
16. Разложение правильной дроби на простейшие
Правильные дроби следующих четырех типов называются простейшими (или элементарными) дробями:
I. ![]()
II. ![]()
III. ![]()
IV. ![]()
При
этом предполагается, что A, B, p, q -
действительные числа, а квадратный
трехчлен ![]() в
дробях III и IV типов не имеет действительных
корней (т.е.
в
дробях III и IV типов не имеет действительных
корней (т.е. ![]() ).
).
Каждая
правильная дробь может быть представлена
в виде суммы простейших дробей указанных
четырех типов. А именно: если знаменатель
данной правильной дроби ![]() разложен
на неповторяющиеся линейные и квадратные
множители
разложен
на неповторяющиеся линейные и квадратные
множители
![]()
где ![]() -
натуральные числа, то эту дробь можно
представить в виде следующей суммы
простейших:
-
натуральные числа, то эту дробь можно
представить в виде следующей суммы
простейших:
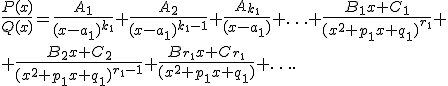
Коэффициенты ![]() в
разложении находятся с помощью метода
неопределенных коэффициентов или
метода частных значений.
в
разложении находятся с помощью метода
неопределенных коэффициентов или
метода частных значений.
17. Интегрирование рациональных дробей
Рациональной
дробью называется дробь вида ![]() ,
где P(x)
и Q(x)
– многочлены. Рациональная дробь
называется правильной, если степень
многочлена P(x)
ниже степени многочлена Q(x);
в противном случае дробь называется
неправильной.
Пусть
необходимо найти интеграл от неправильной
рациональной дроби. При помощи деления
(по правилу деления многочленов)
неправильную рациональную дробь можно
представить в виде суммы целой
рациональной функции и правильной
рациональной дроби. Например,
,
где P(x)
и Q(x)
– многочлены. Рациональная дробь
называется правильной, если степень
многочлена P(x)
ниже степени многочлена Q(x);
в противном случае дробь называется
неправильной.
Пусть
необходимо найти интеграл от неправильной
рациональной дроби. При помощи деления
(по правилу деления многочленов)
неправильную рациональную дробь можно
представить в виде суммы целой
рациональной функции и правильной
рациональной дроби. Например, ![]() .
Затем знаменатель правильной дроби
разлагается на множители вида
.
Затем знаменатель правильной дроби
разлагается на множители вида ![]() ,
а правильная дробь разлагается на сумму
элементарных дробей следующим
образом:
,
а правильная дробь разлагается на сумму
элементарных дробей следующим
образом: