51. Ряд маклорна и разложение функций в этот ряд

1. Разложение функции f(x)=e^x в ряд Маклорена.f(x)=f′(x)=f″(x)=…=f⁽ⁿ⁾(x)=…=e^x. f(0)=f′(0)=f″(0)=…=f⁽ⁿ⁾(0)=…=1. Составим для функции f(x)=e^x формально ряд Маклорена: 1+  . Найдём области сходимости этого ряда.  при любых x, следовательно, областью сходимости ряда является промежуток  (-∞;+∞). Заметим, что так как ряд сходится абсолютно, то    при любых хи тем более   при любых х. Так как f⁽ⁿ⁺¹⁾(x)=e^x и f⁽ⁿ⁺¹⁾(с)=e^с, то  =e^c =0. Таким образом, имеет место разложение при x (-∞;+∞)

e^x=1+  .     (32)

ри использовании рядов, называемых рядами Маклорена (=Макларена), смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование. Теорема Маклорена (ряд Маклорена (=Макларена)) имеет вид:

52. Ряд Тейлора и разложение функции в этот ряд

Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций. Пусть функция   бесконечно дифференцируема в некоторой окрестности точки  . Формальный ряд

называется рядом Тейлора функции   в точке  .

Ряд Тейлора в окрестности точки a имеет виды:

1) , где f(x) - функция, имеющая при х=а производные всех порядков. R_n - остаточный член в ряде Тейлора определяется выражением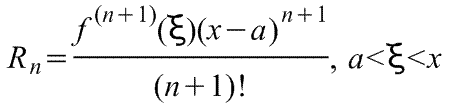 

2)

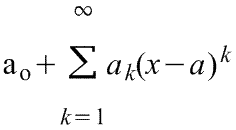
k-тый коэффициент (при х_k) ряда определяется формулой

53. Приминение рядов для вычисления определенных интегралов

Рассмотрим разложение функции в степенной ряд: Для того, чтобы вычислить приближенное значение функции в заданной точке х, принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n членов (n – конечное число), а остальные слагаемые отбрасывают: Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток r_n(x). Для этого применяют следующие приемы: если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена.

если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.

в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа:   (или x<c<a).