1. Функция нескольких переменных
Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.
Обычно функция нескольких переменных задается явным аналитическим способом. Например: z=3x+5y2,u=xy+z2 и т.д.
Встречается также и неявное задание таких функций, например: z-2x-sinxy=0. Упорядоченная пара чисел (x,y) может рассматриваться как точка на плоскости, т.е. Z есть функция точки (x,y). Чтобы задать функцию z=f(x,y), надо не только указать правило нахождения z по заданным x и y, но и то множество (называемое областью задания функции) пар значений, которые могут принимать аргументы x и y.
2. Частное и полное приращение
Полное приращение функции Dz=f(x+Dx, y+Dy)-f(x,y)
Частное приращение функции Dx z=f(x+Dx)-f(x,y) Dy z=f(x,y+Dy)-f(x,y) Вообще, полное приращение функции не равно сумме частных приращений. Пример. z=xy. Dx z=(x+Dx)y-xy=yDx Dy z=x(y+Dy)-xy=xDy Dz=(x+Dx)(y+Dy)-xy=yDx+xDy+DyDx № Dy z+Dx z.
3.
Предел
и непрерывность функции двух переменных
исло А называется
пределом функции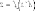 
в
точке 
(или
при 
и 
),
если для любого сколь угодно малого
положительного числа 
найдется
положительное число 
такое,
что для всех точек 
,
отстоящих от точки
на
расстояние, меньшее чем
,
выполняется неравенство
.
Обозначается
предел 
.
Определение
2. Функция 
называется
непрерывной в точке
,
если предел функции в этой точке
существует и 
.
Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва.
На функции нескольких переменных переносятся все свойства и методы теории пределов функции одной переменной.
4. Частные производные Функции 2-х переменных
Рассмотрим
функцию двух переменных 
.
Зафиксируем значение одного из ее
аргументов, например 
,
положив 
.
Тогда функция 
есть
функция одной переменной 
.
Пусть она имеет производную в
точке 
:
Значение
этого выражения показывает, как быстро
меняется значение функции при сдвиге
аргумента в направлении вектора 
.
Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.
.
Данная производная называется частной
производной (или частной производной
первого порядка) функции
по
в
точке 
и
обозначается одним из следующих
символов: 
; 
; 
; 
.
Разность 
называется
частным приращением по
функции
в
точке
и
обозначается символом 
:
.
Учитывая приведенные обозначения, можно записать
.