4. Сортировка данных

Пусть имеется некоторая последовательность элементов произвольного типа (массив или связный список). Сортировкой называется расположение элементов этой последовательности согласно определённому линейному отношению порядка.

1. Пирамидальная сортировка

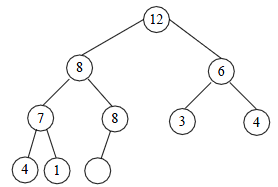
В алгоритме пирамидальной сортировки используется специальная структура данных – пирамида - двоичное дерево, в вершинах которого размещаются заданные нам элементы. При этом должны выполняться следующие требования:

* все уровни, за исключением последнего, должны быть заполнены полностью

* последний уровень (т.е. уровень листьев дерева) может быть заполнен частично, но обязательно слева направо без пропусков

* основное свойство пирамиды: ни один элемент в пирамиде не может быть больше своего родителя

Первая фаза сортировки пирамидой. На первой фазе мы преобразуем исходную последовательность в пирамиду. Как правило, пирамида строится прямо в исходном массиве, и дополнительная память не требуется.

Вторая фаза сортировки пирамидой. На второй фазе полученная пирамида преобразуется в отсортированный массив. Это делается следующим образом. Из основного свойства пирамиды следует, что максимальный элемент находится на её вершине, то есть это элемент а[0]. Поменяем местами элемент а[0] с последним элементом массива - а[п-1]. В результате а[0] встанет на своё конечное место (действительно, раз он наибольший, то после сортировки должен стоять в самом конце).

Чтобы этот элемент больше не рассматривать, уменьшим на 1 длину массива (исходную длину мы предварительно запомним).

Наконец, вызвав функцию downheap() для элемента а[0], мы снова получим пирамиду, только в ней будет на один элемент меньше.

Выполняя в цикле вышеперечисленные действия, мы будем получать отсортированную последовательность, начиная с конца массива. После (п-1) итераций, мы. очевидно, получим полностью отсортированную последовательность.

сложность второй фазы и всего алгоритма — Q(n-log n).

один из недостатков алгоритма сортировки пирамидой состоит в том. Что он не является устойчивым. Преимущества - алгоритм не использует дополнительной памяти, работает одинаково хорошо для среднего и худшего случая.

2. Сортировка слиянием

посмотрим, как можно эффективно слить две уже отсортированных последовательности) в одну общую, также отсортированную. Для этого можно поступить следующим образом. Сравним первые элементы двух последовательностей, меньший из них извлечём и поместим на выход. Так будем продолжать до тех пор. пока одна из последовательностей не опустеет. После этого остаётся только добавить остаток второй последовательности в конец результирующей.

Например, пусть заданы последовательности <2,5,8> и <3, 4>. Сначала сравним элементы 2 и 3, меньший из них 2 - он станет первым элементом результата, а у нас остаётся <5,8> и <3,4>. Теперь 3 меньше чем 5. 3 уходит в результат, у нас остаётся <5,8> н <4>. На следующем шаге 4 уходит, и вторая последовательность становится пустой. Для завершения слияния остаток первой последовательности уходит в результат.

Рекурсивная реализация данного алгоритма очень легка н проста для понимания. Чтобы отсортировать массив, мы разбиваем его на две примерно равные части, рекурсивно сортируем каждую из них. после чего сливаем отсортированные части и получаем результирующий отсортированный массив.

Большим недостатком данного алгоритма является необходимость выделения памяти под вспомогательный массив, куда помешаются результаты слияния двух половинок исходного массива.

сложность всего алгоритма — Q(n-log n).