35.Классификация средних величин

Средняя-обобщающая мера вариационного признака, к-я х\р уровень признака в расчёте на единицу совокупности. Условием испол.ср.явл.наличие качественно однородной совокупности и достаточно большой объём данных. В з\в от ремаемых задач испол.:

Средние арифметические

Простая

взвешенная по показателям тяги f_i

для дискретного ряда

для интервального ряда

для сгруппированных данных

Средняя гармоническая

простая

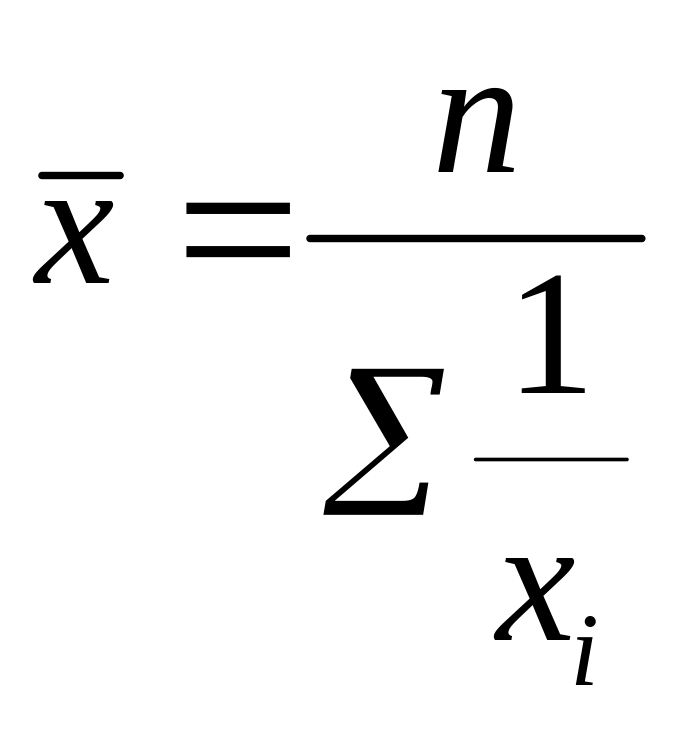
взвешенная

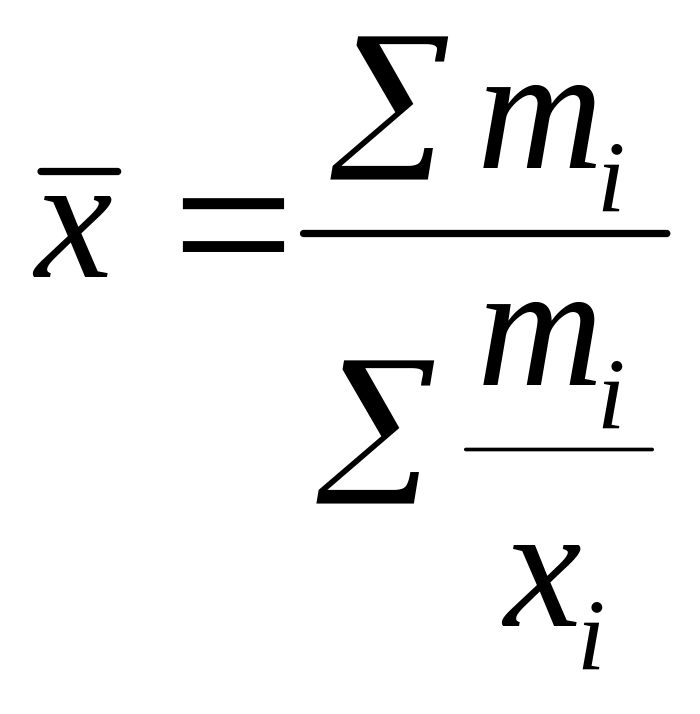
Средняя геометрическая

Средняя степенная

Средняя хронологическая

Средняя квадратическая

36. Анализ эк-х процессов на основе парного кореляционно-регрессионного анализа (кра).

Парная кореляция изучает взаимосвязи фак-тора и результативного признака. Парный КРА проводится по следующим этапам:

1) для исходных данных представленных в виде таблицы определяют поле кореляции; по полу-ченному полю кореляции строят линию регре-сии; 2)определяют уравнение регресии на основе имеющейся таблицы; 3)расчитывают тесноту взаимосвязи на основе коэф-та кореляции, анализируют полученное значение коэф-та кореляции [-1;1]. Если r<0, то связь обратная; если r>0, то связь прямая; если r=0 – взаимосвязь отсутствует; если r=1 – связь тесная.

4)На основе получ значения r осуществляют качественную хар-ку тесноты взаимосвязи используя шкалу Чеддока. 5)Оценивают адекват-ность полученного уравнения регрессии, для этого расчитывают коэф-т детерминации: Д=г2*100%. Этот коэф-т показывает в процент-ном отношении влияние выбранного фактора на результативный признак. Если Д50%, тоуравне-ние регрессии считается адекватным и может быть рекомендовано для практического исполь-зования. Если Д<50% - неадекватно, необходимо использовать или другое уравнение или увели-чить кол-во исх.данных.

37.Относительные показатели вариации.

Вариация – это изменение признака у единиц совокупности. Для колич-ной оценки вариации или колеблемости признака используются след. пок-ли:

1.размах вариации хар-ет амплитуду колебаний W=Xmax – Xmin, где

Xmax, Xmin – соответственно max и min значения признака. Преимущество показателя – легкость в применении, недостаток – его аеличина зависит только от крайних точек.

2. среднее линейное отклонение (Л) показ. средн. отклонение отдельн. вариантов от их средней величины и рассчит-ся как средн. арифметич. Для несгруппиров. данных исп-ют ср. арифм. простую форму, для сгруппиров. – взвешенную.

Простая форма:

Л=Σ│х - х− │/ n , где х – отдельное значение признака, х− - среднее значение признака, n – число единиц совок-ти.

Взвешенная форма:

Л=Σ(х - х− )f/ Σf , где х – отдельное значение признака, х− - среднее значение признака, f – частоты (веса).

3.дисперсия показ. средние квадратич. отклонения отдельных вариантов от их средн. величины. Это теоретич. вел-на, не имеет единиц измерения, используется для расчета средн. квадратич. отклонения. Дисперсия имеет 2 формы: простую (для несгруппир. данных). δ = √Σ(х - х− )² / n, где х – отдельное значение признака, х− - среднее значение признака, n – число единиц совок-ти.

- и взвешенную (для сгруппир. данных):

δ = √ Σ(х - х− )² f / Σf ,где х – отдельное значение признака, х− - среднее значение признака, f – частоты (веса).

5.коэффициент вариации – это проц-ное отн-ение средн. лин-ого или ср. квадратич. откло-ния к средн. величине признака.

V^л = Л / х− * 100 (линейн.)

V^δ = δ / х− * 100 (квадратич.)