Имитационное моделирование спроса на дополнительные услуги сотовой связи

Экономико-математические модель (ЭММ) - математическое описание экономического процесса или объекта, произведенное в целях их исследования и управления ими: математическая запись решаемой экономической задачи.

Одной из первых была модель воспроизводства, разработанная французским ученым Ф. Кенэ еще в XVIII в. А в XX в. первая общая модель развивающейся экономики была сконструирована Дж. фон Нейманом. Значительный опыт построения ЭММ накоплен отечественными учеными, применявшими их для анализа экономических процессов, прогнозирования и планирования во всех звеньях и на всех уровнях экономики, вплоть до планирования развития народного хозяйства страны в целом, особенно перспективного.

Принято подразделять ЭММ на две большие группы:

- модели, отражающие преимущественно производственный аспект экономики;

- модели, отражающие преимущественно социальные аспекты экономики.

Из моделей первой группы можно назвать модели долгосрочного прогноза сводных показателей экономического развития, межотраслевые модели, отраслевые модели оптимального планирования и размещения производства, а также модели оптимизации структуры производства в отраслях.

Из моделей второй группы наиболее разработаны модели, связанные с прогнозированием и планированием доходов и потребления населения, демографических процессов.

Во всех случаях необходимо, чтобы модель содержала достаточно детальное описание объекта, позволяющее, в частности, осуществлять измерение экономических величин и их взаимосвязей, чтобы были выделены факторы, воздействующие на исследуемые показатели.

Пример: формула, по которой определяется на заводе потребность в материалах, исходя из норм расхода, есть ЭММ.

Если количество видов изделий обозначить через n, нормативы расхода — a_i, количество изделий каждого вида — x_i, то модель запишется так:

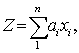
Кроме того, полезно записать условия, в которых она действительна, т. е. ограничения модели (напр., лимиты на те или иные материалы). Строго говоря, расчет по такой формуле не даст точного результата: потребность в материалах может зависеть также от случайных изменений в размерах брака и отходов, от страховых запасов и т. д. Но в общем она зависит именно от указанных двух видов величин: норм расхода материала и объемов выпуска продукции. Первые из них в данном случае называются параметрами модели, вторые — переменными модели.

Такая модель называется описательной, или дескриптивной; она описывает зависимость расхода (потребности в материале) от двух факторов — количества изделий и расходных норм. Большое значение в экономике имеют оптимизационные модели (или оптимальные). Они представляют собой системы уравнений, равенств и неравенств, которые кроме ограничений (условий) включают также особого рода уравнение, называемое функционалом, или критерием оптимальности. С помощью такого критерия находят решение, наилучшее по какому-либо показателю, напр. минимум затрат на материалы при заданном объеме продукции или, наоборот, максимум продукции (или прибыли) при заданных ограничениях по ресурсам и т. д.

Напр., можно попытаться найти такой план работы цеха, который при заданном объеме материалов (т. е. их расход не должен быть больше какой-то величины, допустим, B) гарантирует наибольший объем продукции. Единственное, что надо при этом знать дополнительно — цену единицы продукции pi. Тогда модель будет записываться так:

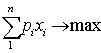
при условии

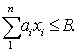
Кроме того, обязательно надо учесть, что искомые величины объемов производства каждого изделия не должны быть отрицательными:

x_i ≥ 0, i = 1, 2, ..., n.

Мы получили элементарную оптимизационную модель, относящуюся к типу моделей линейного программирования. Решив эту модель, т. е. узнав значения всех x_i, от 1-го до n-го, мы получим искомый план.

Важное свойство ЭММ — их применимость к разным, на первый взгляд непохожим ситуациям. Напр., если в приведенном примере через a_i обозначить нормы внесения удобрений, а через x_i — размеры участков, то та же самая формула покажет общий объем потребности в удобрениях. Точно такую же формулу можно применить к расчету затрат семьи на покупку разных продуктов и во многих других случаях.

Модель может быть сформулирована тремя способами:

1) в результате прямого наблюдения и изучения некоторых явлений действительности (феноменологический способ),

2) вычленения из более общей модели (дедуктивный способ),

3) обобщения более частных моделей (индуктивный способ).

Подобные модели, в которых описывается моментное состояние экономики, называются статическими, те же, которые показывают развитие объекта моделирования, — динамическими. 

Модели могут строиться не только в виде формул, как рассмотренные здесь (это называется аналитическим представлением модели), но и в виде числовых примеров (численное представление), в форме таблиц (матричное представление) и в форме особого рода графов (сетевое представление модели).

Соответственно различают модели числовые, аналитические, матричные, сетевые.

 

Метод сценариев.

Сценарий представляет собой набор прогнозов по каждому решению, ее реализации, по возможным положительным и отрицательным последствиям. Сценарии в принятии управленческих решений похоже на литературные сценарии и содержат пролог (вступление, обоснование), основная часть (развитие ситуации), эпилог (последствия). При разработке управленческих решений метод сценариев дополняется ситуационным анализом.

Типовая процедура разработки сценария (шаг, этап):

1. Руководитель составляет подробное описание задания (цель, ситуация, проблема);

2. Работникам поручается разработка вариантов решения проблемы;

3. Специалисту с литературными способностями поручают составить сценарий;

4. Текст сценария распространяется по всем участникам процесса разработки решения;

5. Проведение совещания по обсуждению сценария;

6. Составление окончательного сценария для ввода в базу данных организации.

Метод сценариев применяется в ситуациях, когда необходимо обеспечить высокую вероятность результата и свести к минимуму потери.

Разновидности метода сценария:

1. Метод получения согласования мнения. Сценарий разрабатывается группой, коллективом экспертов (метод Делфи). Применяется по отношению к крупным знаковым событиям в будущем.

2. Метод повторяющегося объединения независимых сценариев.

Суть: по каждому аспекту сложной проблемы разработать сценарий, затем они объединяются и формируют общий сценарий развития ситуации.

Применяется к сложным проблемам.

Плюсы: углубленный анализ всех аспектов ситуации.

Минусы: согласование этих сценариев.

3. Метод матриц взаимо влияний. Кардон и Хелмер – разработали.

Суть: определение на основе экспертных оценок потенциального взаимовлияния событий.

Плюсы: рассмотрение множества комбинаций событий.

Минусы: большая трудоемкость и корректная обработка результатов.

Метод сценариев относят к анализу возможного, а не вероятного будущего. Сценарий привязан к реальным возможностям.

Содержательная часть сценария включает:

1. История развития объекта (явления, процесса).

2. Текущая ситуация.

3. Цель развития объекта.

4. Действующие лица.

5. Психологический конфликт.

6. Проблема (техническая, социальная).

7. Набор мероприятий, решений.

8. Предполагаемые результаты и последствия.

Условия эффективности метода сценария:

1. Правильное соотношение содержательной и количественной информации. 70% на 30% - идеал.

2. Разрабатывается для большой группы людей или организации.

3. Наглядность методов сценария.

4. Кадровое обеспечение.

Модификацией метода сценария является метод дерева решений, который позволяет визуально оценить результаты различных решений и выбрать наилучший их набор. Применяется для типовых управленческих процессов, если накоплен обширный опыт и имеется достаточно информации о решениях, условиях и будущих результатов. Метод дерева решений применяется при разработке компьютерных игр на выбор стратегии.