
- •Раздел 1 «Общие основы теории принятия решений. Этапы процесса рпур»
- •3 Варианта иерархии решений:
- •2. Риск и неопределенность, сопутствующие решениям. Классификация рисков. Сущность стратегического риск-менеджмента. Способы снижения риска на стадиях разработки и реализации управленческого решения.
- •3. Модель процесса подготовки и принятия управленческого решения. Виды моделей принятия решений. Этапы разработки и принятия управленческих решений.
- •Графическая схема модели (упрощенная)
- •Содержание основных этапов принятия и реализации решения
- •Исходных данных;
- •Разработка → принятие → реализация
- •8 Типов ситуации в зависимости от параметров
- •Инициативно-целевая.
- •Программно-целевая.
- •6. Разработка альтернатив решений. Анализ внешней и внутренней среды. Метод матрицы swot.
- •7. Этап принятия управленческого решения. Стратегии принятия решений. Многокритериальный выбор и оценочные системы. Согласование и утверждение принятого решения.
- •1. Перечень критериев (набор).
- •2. Оценка сравнительной важности критериев (веса, ранги).
- •Вербально-числовая шкала Харрингтона
- •4. Принципы выбора.
- •8. Этап реализации (исполнения) управленческого решения: сущность и содержание. План мероприятий. Программа реализации. Анализ и оценка результатов исполнения.
- •9. Контроль реализации управленческих решений. Контроллинг. Ответственность руководителя за принятие и реализацию управленческого решения, ее виды и механизм привлечения.
- •10. Эффективность принимаемых управленческих решений и ее виды. Методы оценки и система показателей эффективности управленческих решений.
- •11. Организационно-правовое, кадровое и финансовое обеспечение процесса разработки, принятия и реализации управленческого решения.
- •12. Информационное обеспечение процесса разработки, принятия и реализации управленческого решения. Информационные технологии разработки и принятия решений. Системы поддержки принятия решений.
- •Раздел 2 «Методы разработки и принятия управленческих решений».
- •13. Общая классификация и краткая характеристика методов разработки и принятия управленческих решений.
- •1. Методы, применяемые на этапе диагностики проблемы и формулировки ограничений и критериев.
- •2. Методы, применяемые на этапе определения альтернатив.
- •14. Методы прогнозирования и планирования при разработке управленческих решений в условиях риска. Методы стратегического планирования.
- •К основным методам планирования относятся:
- •В последнее время особую популярность приобрели такие методы планирования, как:
- •Анализ чувствительности может использоваться:
- •Морфологический ящик
- •Расширение поискового поля с помощью морфологического анализа
- •Морфологическая таблица (ящик)
- •Решение:
- •16. Методы оптимизации при принятии решений: сущность и общая характеристика. Линейное и целочисленное программирование. Типовые задачи оптимизации.
- •Решение с помощью теории графов.
- •Модификации транспортной задачи: Транспортная задача в сетевой постановке.
- •Транспортная задача с ограничениями пропускной способности.
- •Многопродуктовая транспортная задача.
- •Особые требования:
- •1. Очный опрос
- •2. Заочный опрос
- •Методы получения количественных оценок
- •Итак, как работает Метод экспертных оценок:
- •2. Методы получения качественных экспертных оценок.
- •Парные сравнения.
- •Метод эвристических вопросов.
- •Метод многомерных матриц.
- •Метод ассоциаций.
- •Метод инверсии.
- •Метод эмпатии (метод личной аналогии)
- •Метод 635.
- •Метод синектики.
- •Метод организованных стратегий
- •Метод «мозгового штурма».
- •Метод Дельфи.
- •20. Методы моделирования в принятии решений: сущность и общая характеристика. Экономико-математические модели. Имитационное моделирование. Метод сценариев.
- •Математической модели;
- •Имитационное моделирование спроса на дополнительные услуги сотовой связи
2. Методы получения качественных экспертных оценок.
а) экспертная классификация. Экспертами определяется: 1) принадлежность объекта исследования определенным классам, типам, видам; 2) перечень признаков объекта исследования, позволяющих отнести его к тому или иному классу, типу, виду и т.д.
Задача классификации с явными диагностическими признаками может быть сформулирована следующим образом.
Дано: N - число диагностических признаков; S i - число упорядоченных и, как правило, вербальных оценок качества на шкале i-гo диагностического признака; Xi ={x 1i ,x 2i ,...,x si } - множество оценок на шкале i-гo признака; Q - количество диагностических классов ( P 1 , P 2 ,..., P Q ), к которым могут принадлежать классифицируемые объекты.
Декартово произведение А шкал признаков определяет множество всех гипотетически возможных состояний, описываемых диагностическими признаками. Состояние a i , принадлежащее А, описывается вектором (а i 1 , а i 2 ,...,а iN), где j -м компонентом является одно из значений на шкале i -г o диагностического признака.
Требуется: на основе знаний эксперта классифицировать все векторы а i отнеся каждый из них к одному или нескольким классам решений.
Особенность задачи: ставится цель - построение полной классификации, т.е. классификации всех возможных состояний объекта исследования.
Подход экспертной классификации предназначен для построения полных, непротиворечивых и точных баз экспертных знаний в задачах отнесения объектов к различным классам решений. Основные черты подхода экспертной классификации :
• структуризация проблемы ;
• предъявление эксперту описаний объектов в привычном для эксперта виде ;
• распространение решений эксперта на другие состояния (объекты ) при помощи отношения доминирования по характерности ;
• проверка информации эксперта на непротиворечивость ; . эффективная стратегия опроса эксперта .
Эксперты должны обладать всей полнотой знаний.
Используются компьютерные технологии. Компьютерные системы построения полных и непротиворечивых баз знаний ставят эксперту вопрос за вопросом до тех пор, пока все состояния (все векторы a i из множества А) не будут отнесены к одному или нескольким классам. Для создания таких баз знаний требуется от одной—двух недель до одного— двух месяцев работы с опытным экспертом (в зависимости от объема базы знаний).
Приведем конкретные данные по системе КЛАСС. Для создания базы знаний по семи коматозным заболеваниям (классифицируются 2304 состояния пациента) потребовалось 12 ч работы эксперта, по 14 болезням, начинающимся с болевого синдрома в области живота (около 20 тыс. состояний), — 60 ч. Разработка первой базы знаний заняла примерно семь дней, второй — около месяца.
Система ДИФКЛАСС позволяет классифицировать в среднем до 700 состояний объекта исследования в час
Система КЛАСС, а также последовавшие за ней системы ДИФКЛАСС, СТЕПКЛАСС и КЛАНШ отличаются друг от друга стратегией предъявления состояний эксперту. Так, в системе КЛАСС осуществляется выбор наиболее информативного состояния. Предполагается, что все возможные ответы эксперта для любого неизвестного состояния объекта равновероятны. Для каждого неклассифицированного состояния вычисляются количества косвенно классифицируемых состояний при всех возможных ответах эксперта. Далее подсчитывается среднее количество, которое и характеризует информативность предъявления конкретного вектора. Компьютер осуществляет перебор всех неквалифицированных на данный момент состояний и выбирает то, для которого ожидаемое среднее количество косвенно классифицированных состояний максимально. Существенно более эффективными (по числу обращений к эксперту) являются методы ДИФКЛАСС и КЛАНШ.
Пример. Определение перечня признаков, адекватно представляющий состояние объекта исследования? Для этой цели разработана человекомашинная процедура АРИАДНА, которая имитирует диалог по телефону между неопытным специалистом, находящимся рядом с объектом исследования и проводящим измерения, и экспертом, находящимся далеко от объекта. Диалог строится таким образом, что компьютер задает вопросы эксперту, использует его ответы для постановки новых вопросов и т.д. Пример такого диалога.
Компьютер: Вас просят помочь в постановке диагноза. Начинающий врач сообщает вам по телефону, что пациент без сознания и что подозревается диабетическая кома. Каким будет ваш первый вопрос?
Эксперт: Начало заболевания — постепенное или внезапное?
Компьютер: А что более характерно для диабетической комы?
Эксперт: Постепенное начало.
Компьютер: Предположим, что начало было постепенное. Каким будет ваш следующий вопрос?
В ходе диалога эксперт называет признаки и их возможные значения, упорядочивает признаки по характерности для данного заболевания, решая привычные для себя задачи постановки диагноза.
В системе АРИАДНА использованы идеи «диагностических игр», предложенные И.М. Гельфандом. Диагностическая игра — эта та же деловая игра, но применяемая конкретно для диагностики методов принятия решения в медицине (диагностика методов диагностики). Эти игры возникли при исследовании способов передачи знаний от опытных врачей новичкам.
Итак, при подобном подходе процедуры структуризации могут быть представлены следующим образом. Компьютер ставит вопросы эксперту, приглашая его классифицировать объект исследования и называть один за другим признаки, используемые при классификации и их возможные значения для каждого класса решений.
Результатом этого этапа является совокупность признаков, необходимая для полной классификации объектов определенного типа, все возможные значения этих признаков, а также перечень классов решений.
б) метод парных сравнений. Варианты рассматриваются в паре, и от пары выбирается предпочтительный;
Психологами доказано, что попарное сопоставление лежит в основе любого выбора (т.е. Вы выбираете продукты, сравнивая их попарно), тем не менее, шкалу порядка часто составляют заранее (не ранжированный ряд) и фиксируют в ней опорные точки, которые называют баллами.
Пример ранжирования шести объектов путем попарного сравнения. Это результат работы одного эксперта, оценивавшего объекты определенным образом. Предпочтение одного объекта перед другим обозначено 1, обратная ситуация - 0.
Таблица 1. Ранжирование шести объектов путем попарного сравнения
Номер объекта |
1 |
2 |
3 |
4 |
5 |
6 |
Итог |
1 |
х |
1 |
0 |
1 |
1 |
1 |
4 |
2 |
0 |
х |
0 |
1 |
1 |
1 |
4 |
3 |
1 |
1 |
х |
1 |
1 |
1 |
5 |
4 |
0 |
0 |
0 |
х |
0 |
0 |
0 |
5 |
0 |
0 |
0 |
1 |
х |
0 |
1 |
6 |
0 |
0 |
0 |
1 |
1 |
х |
2 |
Ранжированный ряд (шкала порядка) для объектов, сравнительная оценка которых приведена в таб. 1, будет иметь вид:
Q4<Q5<Q6<Q2=Q1<Q3.
Если использовать несколько экспертов, то можно получить более точный результат.
Можно использовать более совершенные критерии, например, преимущество определить оценкой 1, худшее качество определить оценкой -1, а равноценное качество определить оценкой 0. Механизм составления ранжированного ряда остается прежним.
Так появилась двенадцатибальная шкала интенсивности землетрясений MSK - 64, минералогическая шкала Мооса, пятибалльная шкала оценки знаний, баллы в фигурном катании и т.д.
в) метод ранговой корреляции (ранжирование альтернативных вариантов по степени предпочтительности). Не более 20 – 30 вариантов.
Экспертный опрос на основе метода ранговой корреляции основан на том, что каждый из m экспертов, участвующих в опросе, присваивает каждому из оцениваемых n объектов (критериев) некоторое ранговое число (оценку). При этом наиболее важный критерий получает ранг (оценку) 1, следующий − ранг 2 и т. д. в порядке убывания значимости. Если число рангов k не совпадает с числом объектов n , то эксперт присваивает разным объектам один и тот же ранг. Через uij обозначается ранговое число, которое i-ый эксперт присвоил j-му объекту, причем i = 1, 2, ...m и j = 1, 2, ...n.
Чаще всего число рангов меньше, чем число оцениваемых объектов ( k < n ), поэтому для обеспечения возможности применения метода ранговой корреляции объектам присваивают так называемые нормированные ранги. В каждой строке ранговым числам присваиваются последовательно неповторяющиеся места, а затем определяется среднее арифметическое суммы мест, которые занимают объекты с одинаковыми рангами. Это значение записывается в новую нормированную матрицу на место соответствующего ранга. Места для удобства подписываются в исходной матрице в верхнем правом углу ячейки.
Пример №1. Пусть пять экспертов о семи объектах экспертизы Q составили такие ранжированные ряды по возрастающей шкале порядка:
эксперт № 1 –
![]()
эксперт № 2 –
![]()
эксперт № з –
![]()
эксперт № 4 –
![]()
эксперт № 5 –
![]()
Место объекта в ранжированном ряду называется его рангом. Численное значение ранга в ряду возрастающей шкалы порядка увеличивается от 1 до t. В нашем примере t=1.
4. Определяются суммы рангов каждого из объектов экспертной оценки. В рассматриваемом примере они таковы:

5. На основании полученных сумм рангов строим обобщенный ранжированный ряд.
Для нашего примера он имеет вид
6. Обобщенные экспертные оценки качества рассматриваемых объектов экспертизы, т.е. коэффициенты их весомости, рассчитываются по формуле:
 (1)
,
(1)
,
где n – количество экспертов; m - число оцениваемых показателей;
![]() –
коэффициент
весомости j-го показателя в рангах
(баллах), который дал
–
коэффициент
весомости j-го показателя в рангах
(баллах), который дал
i-ый эксперт.
Расчеты по формуле (1) для рассматриваемого примера дают следующие результаты:
 .
.
Анализируя полученные экспертным методом оценки качества, можно не только указать, какой объект лучше или хуже других, но и на сколько.
Пример №2. Рассмотрим пример, когда 5 экспертов оценивают 6 критериев по четырехбалльной системе, т. е. наименее важному критерию присваивается ранг, равный 4. Тогда результаты экспертного опроса можно представить в виде таблицы 1.
Таблица 1

Например, для первого эксперта ранг 1 повторяется два раза, т. к. он присвоен третьему и пятому объектам (К4 и К10), которые, соответственно, имеют места 1 и 2. Следовательно, нормированный ранг этих объектов, представляющий собой среднее арифметическое их мест, равен (1 + 2)/2 = 1,5. Это значение в новой матрице будет стоять в первой строке в третьей и пятой ячейках следующей таблицы 2.
Ранговое число 2 повторяется в первой строке один раз, поэтому ему присваивается следующее место − 3, которое и будет новым нормированным рангом (первая ячейка). Рангу 3 будут присвоены места 4 и 5, а значение (4 + 5)/2 = 4,5 займет в новой матрице вторую и шестую ячейки, где в первоначальной матрице находилась цифра 3. Четвертому рангу, который повторяется один раз, соответствует место 6, которое и будет его нормированным значением.
Во второй строке первый ранг, встречающийся один раз, не меняется; рангу 2 соответствуют места 2–4 и нормированное значение (2 + 3 + 4)/3 = 3; встречающимся по одному разу рангам 3 и 4 соответствуют нормированные значения, равные их местам, соответственно, − 5 и 6.
Таким же образом определяются нормированные ранги и для остальных объектов. В результате нормирования матрица приобретает вид таблицы 2. Последняя строка таблицы 2 содержит суммы нормированных рангов для каждого критерия.
Таблица 2
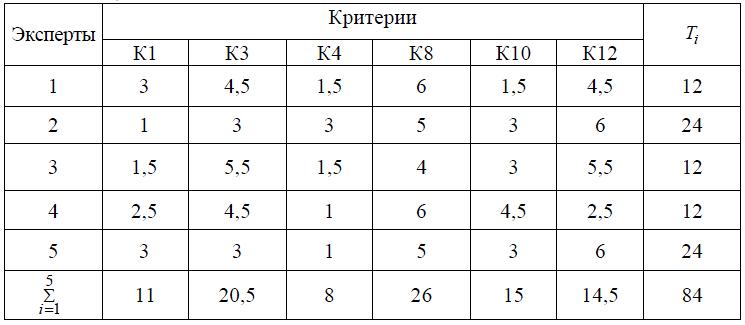
В полученную матрицу вводится столбец Ti , который будет далее использован для оценки достоверности полученных результатов.
Величины Ti рассчитываются по формуле:
![]()
где t j − число повторений j-го рангового числа в i-ой строке.
В примере с четырехбалльной системой оценок число слагаемых в формуле равно 4. Для первого эксперта ранги 1, 2, 3 и 4 повторялись 2, 1, 2 и 1 раз соответственно:
Т1 = (23 –2) + (13 –1) + (23 ––2) + (13 –1) = 12.
Для второго эксперта:
Т2 = (13 –1) + (33 –3) + (13 ––1) + (13 –1) = 24.
Аналогично вычисляются все значения последнего столбца таблицы 2.
Поскольку более важный критерий имеет меньший ранг, то наиважнейшему критерию будет соответствовать минимальная сумма нормированных рангов, т. е. все эксперты оценили этот критерий относительно небольшим числом.
Как видно из вышеприведенного примера, первое место и наибольшее предпочтение должны быть отданы третьему объекту, второе место – первому, третье место – шестому, четвертое место – пятому, пятое место – второму, шестое место – четвертому и т. д.
г) метод векторов предпочтительности. Для каждого варианта эксперт определяет сколько других вариантов превосходит его по предпочтительности. Используется как коллективная оценка (2, 5, 7, 9, 3, 1, 6, 8, 9).
д) дискретные экспертные кривые (линейные графики). Применяются при составлении динамики, прогнозов. По индивидуальным кривым выстраивается общий тренд. Результат – наглядный сценарий развития ситуации.
Инвариантность («стирание различий», обобщение оценок) обеспечивается использованием средних величин:
- средние арифметические;
- средние по Коши (медиана, мода);
- средние по Колмогорову.
Выбор формы и метода проведения экспертного опороса зависит от трех оснований:
1. Цель проведения опроса - что именно должна представить экспертная комиссия в результате своей работы:
- информацию для принятия решения ЛПР
- или проект самого решения?
От ответа на этот вопрос зависит организация работы экспертной комиссии, и он служит первым основанием для разбиения методов.
Если цель – сбор информации для принятия решения, тогда полезен следующий метод постепенного увеличения числа экспертов. Сначала первый эксперт приводит свои соображения по рассматриваемому вопросу. Составленный им материал передается второму эксперту, который добавляет свои аргументы. Накопленный материал поступает к следующему - третьему - эксперту... Процедура заканчивается, когда иссякает поток новых соображений.
Если цель – подготовка проекта самого решения, то применяются математические методы в экспертных оценках.
2. Число туров экспертного опроса. Экспертизы могут включать один тур, два, три или неопределенное число туров. Чем больше туров, тем более тщательным является анализ ситуации, поскольку эксперты при этом обычно много раз возвращаются к рассмотрению предмета экспертизы. Но одновременно увеличивается общее время на экспертизу и возрастает ее стоимость. Можно уменьшить расходы, вводя в экспертизу не всех экспертов сразу, а постепенно. Так, например, если цель состоит в сборе аргументов "за" и "против", то первоначальный перечень аргументов может быть составлен одним экспертом. Второй добавит к нему свои аргументы. Суммарный материал поступит к первому и третьему, которые внесут свои аргументы и контраргументы. И так далее - добавляется по одному эксперту на каждый новый тур.
3. Предпочтения в форме общения экспертов: отсутствие общения - заочное анонимное общение - заочное общение без анонимности - очное общение с ограничениями - очное общение без ограничений.
При отсутствии общения эксперт высказывает свое мнение, ничего не зная о других экспертах и об их мнениях. Он полностью независим, что и хорошо, и плохо. Обычно такая ситуация соответствует однотуровой экспертизе. Заочное анонимное общение, например, как в методе Дельфи, означает, что эксперт знакомится с мнениями и аргументами других экспертов, но не знает, кто именно высказал то или иное положение. Следовательно, в экспертизе должно быть предусмотрено хотя бы два тура. Заочное общение без анонимности соответствует, например, общению по Интернету. Все варианты заочной экспертизы хороши тем, что нет необходимости собирать экспертов вместе, следовательно, находить для этого удобное время и место.
При очных экспертизах эксперты говорят, а не пишут, как при заочных, и потому успевают за то же время сказать существенно больше. Очная экспертиза с ограничениями весьма распространена. Это - собрание, идущее по фиксированному регламенту.
Примером является военный совет в императорской русской армии, когда эксперты (офицеры и генералы) высказывались в порядке от младшего (по чину и должности) к старшему.
Наконец, очная экспертиза без ограничений - это свободная дискуссия. Все очные экспертизы имеют недостатки, связанные с возможностями отрицательного влияния на их проведение социально-психологических свойств и клановых (партийных) пристрастий участников, а также неравенства их профессионального, должностного, научного статусов.
Пример: Представьте себе, что соберутся вместе 5 лейтенантов и 3 генерала. Независимо от того, какая информация имеется у того или иного участника встречи, ход ее предсказать нетрудно: генералы будут беседовать, а лейтенанты - помалкивать. При этом вполне очевидно, что лейтенанты получили образование позже генералов, а потому обладают полезной информацией, которой нет у генералов.
Комбинация различных видов экспертизы. Реальные экспертизы часто представляют собой комбинации различных описанных выше типов экспертиз.
Пример: защита студентом дипломного проекта. Сначала идет многотуровая очная экспертиза, проводимая научным руководителем и консультантами, в результате студент подготавливает проект к защите. Затем два эксперта работают заочно - это автор отзыва сторонней организации и заведующий кафедрой, допускающий работу к защите. Обратите внимание на различие задач этих экспертов и объемов выполняемой ими работы - один пишет подробный отзыв, второй росписью на титульном листе проекта разрешает его защиту. Наконец - очная экспертиза без ограничений (для членов ГАК - государственной аттестационной комиссии). Дипломный проект оценивается коллегиально, по большинству голосов, при этом один из экспертов (научный руководитель) знает работу подробно, а остальные - в основном лишь по докладу. Отметим, что мнения экспертов учитываются с весами, а именно, мнения членов ГАК - с весом 1, мнения всех остальных - с весом 0 (совещательный голос). Таким образом, имеем сочетание многотуровой и однотуровой, заочных и очных экспертиз. Подобные сочетания характерны для многих реально проводящихся экспертиз.
Методы обработки экспертных оценок. Информация, полученная от экспертов, в целях минимизации погрешностей и влияния субъективного фактора обрабатывается с помощью специальных логических и математических процедур и преобразуется в форму, удобную для выбора решения.
Обработка результатов экспертного опроса предполагает:
Определение согласованности мнений экспертов.
Согласованность мнений экспертов определяется по коэффициенту конкордации (согласия) Кендалла. В отношении него рассчитывается дисперсия (отклонение).
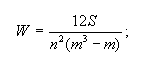
где S - сумма квадратов отклонений всех оценок рангов каждого объекта экспертизы от среднего значения; n - число экспертов; m - число объектов экспертизы.
Коэффициент конкордации изменяется в диапазоне 0<W<1, причем 0 - полная несогласованность, 1 - полное единодушие. Значение коэффициента = 1, если мнения экспертов абсолютно совпадают. Минусы: эксперты являются зависимыми и заранее договорились. Если коэффициент = 0, то это означает полную рассогласованность мнений экспертов. Минусы: эксперты не компетентны.
Пример. Необходимо определить степень согласованности мнения пяти экспертов, результаты ранжирования которыми семи объектов приведены в таблице.
Номер объекта экспертизы |
Оценка эксперта |
Сумма рангов |
Отклонение от среднего |
Квадрат отклонения |
||||
1 |
2 |
3 |
4 |
5 |
||||
1 |
4 |
6 |
4 |
4 |
3 |
21 |
1 |
1 |
2 |
3 |
3 |
2 |
3 |
4 |
15 |
-5 |
25 |
3 |
2 |
2 |
1 |
2 |
2 |
9 |
11 |
121 |
4 |
6 |
5 |
6 |
5 |
6 |
28 |
8 |
64 |
5 |
1 |
1 |
3 |
1 |
1 |
7 |
-13 |
169 |
6 |
5 |
4 |
5 |
6 |
5 |
25 |
5 |
25 |
7 |
7 |
7 |
7 |
7 |
7 |
35 |
15 |
225 |
Итого |
х |
х |
х |
х |
х |
140 |
х |
630 |
Оцениваем среднеарифметическое число рангов:
Qср = (21 + 15 + 9 + 28 + 7 + 25 + 35)/7 = 140/7= 20.
Затем оцениваем сумму квадратов отклонений от среднего: S = 630. Определяем величину коэффициента конкордации:
W = 12 * 630 / 52 * (73 - 7) = 12*630/25*(343-7) = 0,9.
Вывод: различные мнения экспертов в данном примере незначимы.
Обобщение оценки объектов экспертизы.
Определение зависимостей между суждениями экспертов.
Определение относительных весов объектов экспертизы.
Оценка надежности результатов экспертизы.
Математические методы обработки экспертных мнений:
Математическое ожидание: усредненная оценка мнений экспертов с учетом случайных элементов (вероятности).
Пусть задан закон распределения случайной величины x.
-
x
х1
х2
х3
¼
хn
P
p1
p2
p3
¼
pn
Математическое ожидание Мx (или М(x)) случайной величины x определяется формулой
![]()
Пример. Пусть в некотором магазине, торгующем электробытовой техникой, получены статистические данные о числе проданных холодильников в каждый день месяца (условно считаем, что месяц состоит из 30 рабочих дней). Эти данные собраны в таблицу:
-
Количество проданных холодильников
0
1
2
3
4
5
Число дней, в которые было продано столько холодильников
3
7
8
9
2
1
По этой таблице легко подсчитать число холодильников, проданных в магазине за месяц: 0×3+1×7+2×8+3×9+4×2+5×1 = 63. Чтобы подсчитать среднее число холодильников, продававшихся в один день месяца, нужно эту сумму разделить на 30, в результате получим 2,1. Если в приведенной таблице каждое число второй строки поделить на 30, то получится последовательность дробей:
![]() ,
каждая из которых представляет собой
так называемую относительную
частоту,
с которой в данный месяц появлялся
приведенный в верхней строке объём
продаж. Очевидно, что если просуммировать
все произведения чисел, стоящих в первой
строке таблицы, на их относительные
частоты, то получится то же среднее
число продававшихся в один день
холодильников:
,
каждая из которых представляет собой
так называемую относительную
частоту,
с которой в данный месяц появлялся
приведенный в верхней строке объём
продаж. Очевидно, что если просуммировать
все произведения чисел, стоящих в первой
строке таблицы, на их относительные
частоты, то получится то же среднее
число продававшихся в один день
холодильников:
![]()
Вывод: среднеожидаемое число продаваемых холодильников составляет 2,1 шт. в день.
Оптимизационные задачи («медиана Кемени» - среднее мнение экспертов, которое обеспечивает минимальное отклонение мнений разных кандидатов).
С помощью расстояния Кемени находят итоговое мнение комиссии экспертов. Пусть А1 , А2 , А3 ,…, Ар - ответы р экспертов, представленные в виде бинарных отношений. Для их усреднения используют т.н. медиану Кемени Arg min ∑ D (Ai ,A) , где Arg min - то или те значения А, при которых достигает минимума указанная сумма расстояний Кемени от ответов экспертов до текущей переменной А, по которой и проводится минимизация. Таким образом, ∑ D (Ai ,A) = D (A1 ,A) + D (A2 ,A) + D (A3 ,A) +…+ D (Aр ,A) .
Пример. Рассмотрим пример вычисления медианы Кемени. Пусть дана квадратная матрица (порядка 9) попарных расстояний для множества бинарных отношений из 9 элементов А1 , А2 , А3 ,..., А9 (см. табл.).
Матрица попарных расстояний
0 |
2 |
13 |
1 |
7 |
4 |
10 |
3 |
11 |
2 |
0 |
5 |
6 |
1 |
3 |
2 |
5 |
1 |
13 |
5 |
0 |
2 |
2 |
7 |
6 |
5 |
7 |
1 |
6 |
2 |
0 |
5 |
4 |
3 |
8 |
8 |
7 |
1 |
2 |
5 |
0 |
10 |
1 |
3 |
7 |
4 |
3 |
7 |
4 |
10 |
0 |
2 |
1 |
5 |
10 |
2 |
6 |
3 |
1 |
2 |
0 |
6 |
3 |
3 |
5 |
5 |
8 |
3 |
1 |
6 |
0 |
9 |
11 |
1 |
7 |
8 |
7 |
5 |
3 |
9 |
0 |
Требуется найти в этом множестве медиану для множества из 5 элементов {А2 , А4 , А5 , А8 , А9}.
В соответствии с определением медианы Кемени следует ввести в рассмотрение функцию С(А) = ∑ D(Ai ,A) = D(A2 ,A)+D(A4 ,A)+D(A5 ,A)+D(A8 ,A)+D(A9 ,A), рассчитать ее значения для всех А1 , А2 , А3 ,..., А9 и выбрать наименьшее.
Проведем расчеты: С(А1) = 24, С(А2) = 13, С(А3) = 21, С(А4) = 27, С(А5) = 16, С(А6) = 23, С(А7) = 15, С(А8) = 25, С(А9) = 25.
Из всех вычисленных сумм наименьшая равна 13, и достигается она при А = А2, следовательно, медиана Кемени - это А2.
