Решение с помощью теории графов.

Рассматривается двудольный граф, в котором пункты производства находятся в верхней доле, а пункты потребления — в нижней. Пункты производства и потребления попарно соединяются рёбрами бесконечной пропускной способности и цены за единицу потока  .

К верхней доле искусственно присоединяется исток. Пропускная способность рёбер из истока в каждый пункт производства равна запасу продукта в этом пункте. Цена за единицу потока у этих рёбер равна 0.

Аналогично к нижней доле присоединяется сток. Пропускная способность рёбер из каждого пункта потребления в сток равна потребности в продукте в этом пункте. Цена за единицу потока у этих рёбер тоже равна 0.

Дальше решается задача нахождения максимального потока минимальной стоимости (mincost maxflow). Её решение аналогично нахождению максимального потока в алгоритме Форда — Фалкерсона. Только вместо кратчайшего дополняющего потока ищется самый дешёвый.

При решении несбалансированной транспортной задачи применяют приём, позволяющий сделать ее сбалансированной. Для этого вводят фиктивные пункты назначения или отправления. Выполнение баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц.

Модификации транспортной задачи: Транспортная задача в сетевой постановке.

В этом варианте пункты не делятся на пунктов отправления и пункты потребления, все пункты равноправны, но производство задается положительным числом, а потребление - отрицательным. Перевозки осуществляются по заданной сети, в которой дуги могут соединять любые пункты (включая производитель -> производитель, потребитель -> потребитель). Задача решается слегка измененным методом потенциалов, практически тем же, что и классическая постановка.

Транспортная задача с ограничениями пропускной способности.

Вариант транспортной задачи в сетевой постановке, в котором задается максимальная пропускная способность некоторых дуг. Задача решается слегка усложненным методом потенциалов.

Многопродуктовая транспортная задача.

Вариант транспортной задачи, в которой присутствует несколько продуктов (пункты могут производить/потреблять несколько продуктов). Для некоторых дуг задается ограничение на пропускную способность (без этого ограничения задача распадается на отдельные задачи по продуктам). Задача решается симплекс-методом (используется разложение Данцига-Вулфа, в качестве подзадач используются однопродуктовые транспортные задачи)

17. Вероятностно-статистические методы принятия решений: сущность и общая характеристика. Эконометрические методы. Высокие статистические технологии. Точки роста. Метод статистических игр. Метод стратегических игр.

К вероятностно-статистическим методам относятся:

1. Вероятностно-статистические методы описания неопределенности.

2. Вероятностно-статистические методы принятия решений.

Основа этих методов:

- теория вероятности;

- методы статистического анализа (корреляционный, регрессионный);

- теория нечеткости;

- эконометрические методы;

- метод статистических игр.

Применение вероятностно-статистических методов включает этапы:

1. Переход от реальности к абстрактной математико-статистической схеме (построение моделей, процессов, процедур).

2. Проведение расчетов и получение выводов математическими средствами (в рамках вероятностной модели).

3. Интерпретация математико-статистических методов применительно к реальной ситуации и принятие решения.

Эконометрические методы в составе вероятностно-статистических методов применяются в основном в контролинге, т.е. когда необходимо разнообразная информация и удобные инструменты для ее анализа. Применяются «высокие статистические технологии» для поддержки принятия решений. Особенно к объектам не числовой природы (пример: выбор главной цели организации, сравнение образцов продукции).

К высоким статистическим технологиям относят:

1. Статистика не числовых данных.

2. Статистика интервальных данных.

3. Статистика нечетких данных (≈).

Большое распространение получают «нейронные сети», они используются для построения эконометрических моделей при принятии решений.

Нейронная сеть – специальная компьютерная программа имитирующая работу мозга человека. Состоит из базовых элементов – нейронов. Идея метода восходит к 1940 гг.

Эконометрические инструменты применяемые в вероятностно статистических методах:

1. Описание данных и графическое представление.

2. Углубленный вероятностно статистический анализ.

3. Экспертные исследования.

4. Методы сценария и анализа риска.

Современной эконометрической технологией является «точка роста». Точки роста – ключевые этапы жизненно важных для развития процесса объекта.

Виды точек роста:

1. Непараметрические точки роста, т.е. представлены в виде гипотезы, предположения.

2. Робастность. Это точка ориентированная на отсечение лишнего в результатах наблюдения и на усиление главенствующей тенденции (устойчивость).

3. Бутстреп. Это точка получается в результате размножения выборки наблюдения и собирание их в определенный набор.

4. Интервальные, т.е. «от…и до….».

5. Нечисловые (качественные признаки, ранги, классы, разряды).

Современные статистические технологии включают целый ряд процедур, алгоритмов, выполняемых последовательно, параллельно, по сложной схеме.

Типовая схема статистической технологии

1. Планирование статистического исследования.

2. Организация сбора данных о программе.

3. Непосредственный сбор данных и их фиксация.

4. Первичное описание данных (построение таблиц, диаграмм).

5. Оценка числовых и не числовых параметров, в том числе вариация (колеблемость) зависимости).

6. Проверка статистических гипотез.

7. Более углубленное изучение (многомерный статистический анализ).

8. Проверка устойчивости полученных оценок и выводов.

9. Применение полученных статистических результатов в конкретных прикладных целях.

10. Составление итоговых отчетов для ЛПР и других лиц – не специалистов в эконометрике и статики.

Теория игр. Данный метод служит для моделирования оценки воздействия принятого решения на конкурентов. Изначально была разработана военными с тем, чтобы в стратегии учесть возможные действия противника. В бизнесе игровые модели используются для прогнозирования реакции конкурентов на изменение цен, модификацию и освоение новой продукции, предложения дополнительного обслуживания и т.д. Теория игр используется реже, чем другие модели, так как ситуации в реальном мире очень сложны и часто меняются. Но, тем не менее, теория игр полезна для определения наиболее важных и требующих учета факторов в ситуации принятия решений в условиях конкурентной борьбы. Благодаря применению данной теории организация может прогнозировать действия конкурентов, что является преимуществом и увеличивает конкурентоспособность.

Игра - упрощенная формализованная модель реальной кон­фликтной ситуации. Математически формализация означает, что выработаны определенные правила действия сторон в процессе игры: варианты действия сторон; исход игры при данном вари­анте действия; объем информации каждой стороны о поведении всех других сторон.

Одну играющую сторону при исследовании операций может представлять коллектив, преследующий некоторую общую цель. Однако разные члены коллектива могут быть по-разному инфор­мированы об обстановке проведения игры.

Выигрыш или проигрыш сторон оценивается численно, дру­гие случаи в теории игр не рассматриваются, хотя не всякий выигрыш в действительности можно оценивать количественно.

Игрок - одна из сторон в игровой ситуации. Стратегия иг­рока - его правила действия в каждой из возможных ситуаций игры. Существуют игровые системы управления, если процесс управления в них рассматривается как игра.

Платежная матрица (матрица эффективности, матрица игры) включает все значения выигрышей (в конечной игре).

Пусть игрок 1 имеет т стратегий А_i, а игрок 2 - п стратегий В_j, ( ;  ). Игра может быть названа игрой тхп. Представим мат­рицу эффективности игры двух лиц с нулевой суммой, сопрово­див ее необходимыми обозначениями (табл. 1).

Таблица 1

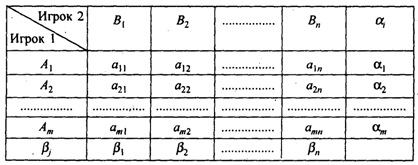
В данной матрице элементы   – значения выигрышей игро­ка 1 – могут означать и математическое ожидание выигрыша (среднее значение), если выигрыш является случайной величи­ной. Величины  ,– соответственно мини­мальные значения элементов  , по строкам и максимальные - по столбцам. Их содержательный смысл будет отражен ниже.

В теории игр не существует установившейся классификации видов игр. Однако по определенным критериям некоторые виды можно выделить.

Количество игроков. Если в игре участвуют две сто­роны, то ее называют игрой двух лиц. Если число сторон больше двух, ее относят к игре п игроков. Наибольший интерес вызыва­ют игры двух лиц. Они и математически более глубоко прорабо­таны.

Количество стратегий игры. По этому критерию игры делятся на конечные и бесконечные. В конечной игре каж­дый из игроков имеет конечное число возможных стратегий. Если хотя бы один из игроков имеет бесконечное число возможных стратегий, игра является бесконечной.

Взаимоотношения сторон. Согласно данному кри­терию игры делятся на кооперативные, коалиционные и бескоа­лиционные. Если игроки не имеют право вступать в соглашения, образовывать коалиции, то такая игра относится к бескоалицион­ным; если игроки могут вступать в соглашения, создавать коали­ции - коалиционной. Кооперативная игра - это игра, в которой заранее определены коалиции.

Характер выигрышей. Этот критерий позволяет клас­сифицировать игры с нулевой и с ненулевой суммой. Игра с ну­левой суммой предусматривает условие: «сумма выигрышей всех игроков в каждой партии равна нулю». Игры двух игроков с нулевой суммой относят к классу антагонистических. Естествен­но, выигрыш одного игрока при этом равен проигрышу другого. Примерами игр с нулевой суммой служат многие экономические задачи. В них общий капитал всех игроков перераспределяется между игроками, но не меняется. К играм с ненулевой суммой также можно отнести большое количество экономических задач. Например, в результате торговых взаимоотношений стран, уча­ствующих в игре, все участники могут оказаться в выигрыше. Игра, в которой нужно вносить взнос за право участия в ней, является игрой с ненулевой суммой.

Вид функции выигрышей. По этому критерию игры подразделяются на матричные, биматричные, непрерывные, выпуклые, сепарабельные и т. д. Поясним суть некоторых из них.

Матричная игра - конечная игра двух игроков с нулевой суммой. В общем случае ее платежная матрица является прямо­угольной (см. табл. 1). Номер строки матрицы соответствует номеру стратегии, применяемой игроком 1. Номер столбца соот­ветствует номеру стратегии игрока 2. Выигрыш игрока 1 являет­ся элементом матрицы. Выигрыш игрока 2 равен проигрышу игрока 1. Как показано в приложении, матричные игры всегда имеют решения в смешанных стратегиях. Они могут быть реше­ны методами линейного программирования.

Биматричная игра - конечная игра двух игроков с ненулевой суммой. Выигрыши каждого игрока задаются своей матрицей, в которой строка соответствует стратегии игрока 1, а столбец — стратегии игрока 2. Однако элемент первой матрицы показывает выигрыш игрока 1, а элемент второй матрицы - выигрыш игро­ка 2. Для биматричных игр так же, как и для матричных, разра­ботана теория оптимального поведения игроков.

Если функция выигрышей каждого игрока в зависимости от стратегий является непрерывной, игра считается непрерывной. Если функция выигрышей выпуклая, то и игра - выпуклая.

Если функция выигрышей может быть разделена на сумму произведений функций одного аргумента; то игра относится к сепарабельной.

Количество ходов. Согласно этому критерию игры можно разделить на одношаговые и многошаговые. Одношаго­вые игры заканчиваются после одного хода каждого игрока. Так, в матричной игре после одного хода каждого из игроков проис­ходит распределение выигрышей. Многошаговые игры бывают позиционными, стохастическими, дифференциальными и др.

Информированность cmoрон. По данному крите­рию различают игры с полной и неполной информацией. Если каждый игрок на каждом ходу игры знает все ранее приме­ненные другими игроками на предыдущих ходах стратегии, такая игра определяется как игра с полной информацией. Если игроку не все стратегии предыдущих ходов других игроков известны, то игра классифицируется как игра с неполной ин­формацией. Мы далее убедимся, что игра с полной информа­цией имеет решение. Решением будет седловая точка при чистых стратегиях.

Степень неполноты и н формации. По этому кри­терию игры подразделяются на статистические (в условиях час­тичной неопределенности) и стратегические (в условиях полной неопределенности).

Игры с природой часто относят к статистическим играм. В статистической игре имеется возможность получения информации на основе статис­тического эксперимента, при котором вычисляется или оценива­ется распределение вероятностей состояний (стратегий) приро­ды. С теорией статистических игр тесно связана теория приня­тия экономических решений.

Под статистическими играми понимается образная игра двух лиц (человек и природа) с использованием человеком дополнительной статистической информации о состоянии природы. Человек это разумный игрок, а природа это пассивный игрок (не разумный). Смысл игры: четко определить выигрыши, потери и риски для человека.

Вне зависимости от сложности решения или сложности средства, используемого для анализа решения, все, принимающие решения, сталкиваются с альтернативами и состоянием природы. Альтернатива — направление действия или стратегия, которая может быть выбрана принимающим решение (например, не брать зонт завтра). Состояние природы — ситуация, на которую принимающий решение не может влиять или имеет очень слабое влияние (например, завтрашняя погода).

Можно построить таблицу решений или платежную таблицу, чтобы помочь компании определить ее альтернативы. Для любых альтернатив и определенного состояния природы имеется следствие или выход, который обычно представляется в денежном выражении. Все альтернативы в примере  записываются в левой части таблицы, а состояния природы записываются в верхней части таблицы, условные значения (платы) находятся внутри таблицы.

Пример - Создаем таблицу для компании, включающую условные значения, которые базируются на следующей информации. Случай благоприятного рынка — большой завод даст чистую прибыль компании 200 тысяч долларов, если рынок неблагоприятный, то чистые потери будут 180 тысяч долларов. А малый завод принесет 100 000-долларовый доход в случае благоприятного рынка; чистые потери в 20 тысяч долларов появятся, если рынок будет неблагоприятным.

Оценки игры.

Рассмотрим матричную игру, представленную матрицей вы­игрышей тхп, где число строк  , а число столбцов   (см. табл. 2.1). Применим принцип получения максимального га­рантированного результата при наихудших условиях. Игрок 1 стремится принять такую стратегию, которая должна обеспечить максимальный проигрыш игрока 2. Соответственно игрок 2 стре­мится принять стратегию, обеспечивающую минимальный вы­игрыш игрока 1. Рассмотрим оба этих подхода.

Подход игрока 1.Он должен получить максимальный гарантированный результат при наихудших условиях. Значит, при выборе отвечающей этим условиям своей чистой страте­гии он должен выбрать гарантированный результат в наихудших условиях, т.е. наименьшее значение своего выигрыша а,., которое обозначим

Чтобы этот гарантированный эффект в наихудших условиях был максимальным, нужно из всех а, выбрать наибольшее зна­чение. Обозначим его а и назовем чистой нижней ценой игры («максимин»):

                                                                  

Таким образом, максиминной стратегии отвечает строка мат­рицы, которой соответствует элемент a_i. Какие бы стратегии ни применял игрок 2, игрок 1 максиминной чистой стратегией га­рантировал себе выигрыш, не меньший, чем a. Таково оптималь­ное поведение игрока 1.

Подход игрока 2. Своими оптимальными стратегиями он стремится уменьшить выигрыш игрока 1, поэтому при каж­дой j-й чистой стратегии он отыскивает величину своего макси­мального проигрыша

                                                                              

в каждом j-м столбце, т.е. определяет максимальный выигрыш игрока 1, если игрок 2 применит j-ю чистую стратегию. Из всех своих n j-х чистых стратегий он отыскивает такую, при которой игрок 1 получит минимальный выигрыш, т.е. определяет чистую верхнюю цену игры («минимакс»):

                                                                  

Чистая верхняя цена игры показывает, какой максимальный выигрыш может гарантировать игрок 1, применяя свои чистые стратегии, - выигрыш, не меньший, чем a. Игрок 2 за счет ука­занного выше выбора своих чистых стратегий не допустит, что­бы игрок 1 мог получить выигрыш, больший, чем b. Таким об­разом, минимаксная стратегия отображается столбцом платеж­ной матрицы, в котором находится элемент b (см. табл. 2.1). Она является оптимальной чистой гарантирующей стратегией игро­ка 2, если он ничего не знает о действиях игрока 1.

Чистая цена игры v - цена данной игры, если нижняя и вер­хняя ее цены совпадают:

                                                      

В этом случае игра называется игрой с седловой точкой.

Пример 1. Определить верхнюю и нижнюю цены при за­данной матрице игры и указать максиминную и минимаксную стратегии. Представим матрицу игры с обозначениями страте­гий b_j, a._j, (табл. 2).

Т а б л и ц а 2

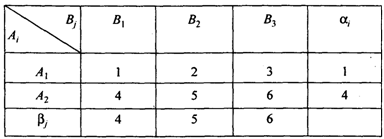
Решение. Определим нижнюю цену игры:

;  ;  (см. столбец  ).

Определим верхнюю цену игры:

;  ;  ;   (см. строку b_j).

Таким образом,  , т.е.

Значит,   – чистая цена игры при стратегиях А₂ и B₁. Следовательно, имеем игру с седловой точкой.

Пример 2. Определим максиминную и минимаксную стра­тегии при заданной матрице эффективности (табл. 3).

Решение. Определим максиминную стратегию:

;  ; 

Максиминная стратегия - строка А₂.

Таблица 3

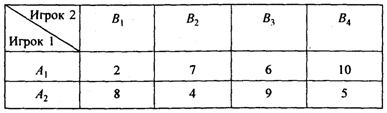
Определим минимаксную стратегию:

Минимаксная стратегия - столбец В₂. Здесь  , следова­тельно, седловой точки нет.

Если матрица игры содержит элемент, минимальный в сво­ей строке и максимальный в своем столбце, то он, как уже сказано выше, является седловой точкой. В этом случае мы имеем игру с седловой точкой.

Пусть в игре с седловой точкой один игрок придерживается седловой точки, тогда другой получит лучший результат, если также будет придерживаться этой точки. Лучшее поведение иг­рока не должно повлечь уменьшение его выигрыша. Зато худшее поведение может привести к этому. В данном случае решением игры являются:

• чистая стратегия игрока 1;

• чистая стратегия игрока 2;

• седловой элемент.

Оптимальные чистые стратегии — это чистые стратегии, об­разующие седловую точку.

В игре без седловой точки, если игрок 1 информирован о стратегии, принятой игроком 2, он сможет принять оптималь­ную стратегию, которая не совпадает с максиминной.

Пример 3. Дана матрица игры

Допустим, игроку 1 стало известно, что игрок 2 принял минимаксную стратегию. Игрок 1 должен выбрать оптимальную стратегию при условии, что B₂  – стратегия игрока 2 (  = 5).

Решение. Определим максиминную стратегию игрока 1:

Стратегия игрока 1 – А₂ - максиминная.

Выберем оптимальную стратегию для игрока 1. Ею будет не максиминная А₂, дающая игроку 1 выигрыш   = 4, а та страте­гия, которая соответствует  . В этом случае его максималь­ный гарантированный выигрыш будет равен верхней цене игры  , поэтому он выберет свою оптимальную стратегию А₁, зная, что игрок 2 выбрал свою стратегию В₂. Таким образом, рас­смотренный пример дает результат, отличный от результата при игре с седловой точкой.

Стратегия является оптимальной, если ее применение обес­печит игроку наибольший гарантированный выигрыш при лю­бых возможных стратегиях другого игрока.

На примере 2.3 показано, что бывают ситуации, когда игрок 1 может получить выигрыш, превосходящий максиминный, если ему известны намерения игрока 2.

При многократном повторении игры в сходных условиях можно добиться гарантированного среднего выигрыша, превос­ходящего для игрока 1 максиминный.

18. Метод экспертных оценок: сущность и общая характеристика. Организация и основные стадии экспертного опроса. Формы проведения экспертного опроса. Догмы согласованности и одномерности. Способы обработки экспертных оценок. Коэффициент «согласия».

Экспертный метод в системе методов принятия управленческих решений.

Сущность экспертных методов (всех) заключается в проведении интуитивно-логического анализа проблемы, выполняемого привлеченными для этих целей специалистами - экспертами, обладающими необходимыми профессиональными знаниями, опытом, интуицией.

Когда прибегают к экспертным методам. В сложных ситуациях выбора ЛПР может не обладать всей необходимой информацией или опытом, что повышает степень риска принятия ошибочного решения. Кроме того, многие проблемы, требующие решения, полностью или частично не поддаются количественному анализу, и, следовательно, не дают возможности использовать методы моделирования. В подобных случаях значительный эффект приносят экспертные технологии.

Экспертные методы делятся на группы:

Эвристические методы. Методы коллективной генерации идей (в т.ч. мозговой штурм).	Эксперты вырабатывают нестандартные оригинальные идеи решения проблем.
Методы экспертных оценок. Метод экспертиз.	Эксперты ОЦЕНИВАЮТ, а не выдвигают (как в эвристических методах) решения, проекты, программы, соревнования, экзамен, обстановку и т.п.
Методы экспертного прогнозирования. Метод сценариев.	Эксперты составляют СЦЕНАРИЙ будущего, определяют последствия вариантов решений и т.п.

Методы экспертных оценок - это методы организации работы со специалистами-экспертами и обработки мнений экспертов. 

Экспертное оценивание — процедура получения оценки проблемы на основе мнения специалистов (экспертов) с целью последующего принятия решения (выбора).

Экспертная оценка — компетентное мнение, мнение эксперта по какой-либо из проблем, находящихся в сфере его компетенции.

Существует две группы экспертных оценок:

• Индивидуальные оценки основаны на использовании мнения отдельных экспертов, независимых друг от друга.

• Коллективные оценки основаны на использовании коллективного мнения экспертов (экспертных комиссий).

Совместное мнение обладает большей точностью, чем индивидуальное мнение каждого из специалистов. Данный метод применяют для получения количественных оценок качественных характеристик и свойств.

Примеры экспертных оценок: индивидуальные - преподаватель единолично ставит отметку студенту, а врач - диагноз больному. Но в сложных случаях заболевания или угрозе отчисления студента за плохую учебу обращаются к коллективному мнению - симпозиуму врачей или комиссии преподавателей. Аналогичная ситуация - в армии. Обычно командующий принимает решение единолично. Но в сложных и ответственных ситуациях проводят военный совет. Один из наиболее известных примеров такого рода - военный совет 1812 г. в Филях, на котором под председательством М.И. Кутузова решался вопрос: "Давать или не давать французам сражение под Москвой?"

 Другой простейший пример экспертных оценок - оценка номеров в КВН. Каждый из членов жюри поднимают фанерку со своей оценкой, а технический работник вычисляет среднюю арифметическую оценку, которая и объявляется как коллективное мнение жюри (ниже увидим, что такой подход некорректен с точки зрения теории измерений).

В фигурном катании процедура усложняется - перед усреднением отбрасываются самая большая и самая маленькая оценки. Это делается для того, чтобы не было соблазна завысить оценку одной спортсменке (например, соотечественнице) или занизить другой. Такие резко выделяющиеся из общего ряда оценки будут сразу отброшены.

Экспертные оценки часто используются при выборе, например:

 - одного варианта технического устройства для запуска в серию из нескольких образцов,

 - группы космонавтов из многих претендентов,

 - набора проектов научно-исследовательских работ для финансирования из массы заявок,

 - получателей экологических кредитов из многих желающих,

 - при выборе инвестиционных проектов для реализации среди представленных, и т.д.

Оценка нескольких технических проектов по их степени соответствия заданному критерию – пример работы целой экспертной комиссии.

Известны следующие методы экспертных оценок:

1. Метод ассоциаций. Основан на изучении схожего по свойствам объекта с другим объектом.

2. Метод парных (бинарных) сравнений. Основан на сопоставлении экспертом альтернативных вариантов, из которых надо выбрать наиболее предпочтительные.

3. Метод векторов предпочтений. Эксперт анализирует весь набор альтернативных вариантов и выбирает наиболее предпочтительные.

4. Метод фокальных объектов. Основан на перенесении признаков случайно отобранных аналогов на исследуемый объект.

5. Индивидуальный экспертный опрос. Опрос в форме интервью или в виде анализа экспертных оценок. Означает беседу заказчика с экспертом, в ходе которой заказчик ставит перед экспертом вопросы, ответы на которые значимы для достижения программных целей. Анализ экспертных оценок предполагает индивидуальное заполнение экспертом разработанного заказчиком формуляра, по результатам которого производится всесторонний анализ проблемной ситуации и выявляются возможные пути ее решения. Свои соображения эксперт выносит в виде отдельного документа.

6. Метод средней точки. Формулируются два альтернативных варианта решения, один из которых менее предпочтителен. После этого эксперту необходимо подобрать третий альтернативный вариант, оценка которого расположена между значений первой и второй альтернативы.

Экспертные оценки получают в ходе экспертного опроса.

Экспертный опрос — разновидность опроса, в ходе которого респондентами являются эксперты — высококвалифицированные специалисты в определенной области деятельности.

Надёжность оценок и решений, принимаемых на основе суждений экспертов, достаточно высока и в значительной степени зависит от организации и направленности процедуры сбора, анализа и обработки полученных мнений.

Сама процедура экспертного опроса предполагает:

• анализ исследуемой ситуации

• выбор группы экспертов

• выбор способа замера экспертных оценок

• процедуру непосредственной оценки работы экспертов

• анализ полученных данных

Может оказаться необходимой также:

• проверка входных данных, используемых для экспертных оценок

• изменение состава экспертных групп

• повторные замеры по тем же вопросам с последующим сопоставлением результатов с объективной информацией, полученной другими методами.

Основные стадии экспертного опроса с точки зрения его организации.

1) Принятие решения о необходимости проведения экспертного опроса и формулировка лицом, принимающим решения (ЛПР) его цели.

 2) Подбор и назначение ЛПР основного состава рабочей группы (РГ).

 3) Разработка РГ и утверждение у ЛПР технического задания на проведение экспертного опроса.

 4) Разработка аналитической группой РГ подробного сценария (т.е. регламента) проведения сбора и анализа экспертных мнений (оценок). 

Сценарий проведения экспертного опроса включает в себя прежде всего  конкретный вид информации, которая будет получена от экспертов (например, слова, условные градации, числа, ранжировки, разбиения или иные виды объектов нечисловой природы). Например, довольно часто экспертов просят высказаться в свободной форме, ответив при этом на некоторые количество заранее сформулированных вопросов. Кроме того, их просят заполнить формальную карту, в каждом пункте выбрав одну из нескольких градаций. Сценарий должен содержать и конкретные методы анализа собранной информации. Например, вычисление медианы Кемени, статистический анализ люсианов, применение иных методов статистики объектов нечисловой природы и других разделов прикладной статистики (о некоторых из названных методов речь пойдет ниже). Эта работа ложится на эконометрическую и компьютерную группу РГ. Традиционная ошибка - сначала собрать информацию, а потом думать, что с ней делать. В результате, как показывает печальный опыт, информация используется не более чем на 1-2%.

 5) Подбор экспертов в соответствии с их компетентностью. На этой стадии РГ составляет список возможных экспертов и оценивает степень их пригодности для планируемого исследования.

 6) Формирование экспертной комиссии. На этой стадии РГ проводит переговоры с экспертами, получает их согласие на работу в экспертной комиссии (сокращенно ЭК). ЛПР утверждает состав экспертной комиссии, возможно, вычеркнув или добавив часть экспертов к предложениям РГ. Проводится заключение договоров с экспертами об условиях их работы и ее оплаты.

 7) Проведение сбора экспертной информации. 

 8) Компьютерный анализ экспертной информации .

 9) При применении согласно сценарию экспертной процедуры из нескольких туров - повторение двух предыдущих этапов.

 10) Итоговый анализ экспертных мнений, интерпретация полученных результатов аналитической группой РГ и подготовка заключительного документа ЭК для ЛПР.

 11) Официальное окончание деятельности РГ, в том числе утверждение ЛПР заключительного документа ЭК, подготовка и утверждение научного и финансового отчетов РГ о проведении экспертного исследования, оплата труда экспертов и сотрудников РГ, официальное прекращение деятельности (роспуск) ЭК и РГ.