Решение:

Для установления связи между величиной цены за 1 м² (факторный признак) и прибылью (результативный признак) произведем сортировку соответствующих столбцов заданных в исходной таблице по возрастанию цены за 1 м² . На основании результатов рабочей таблицы 2 строим сводную таблицу 5 (аналитической группировки организаций) зависимости прибыли от цены за 1 м². Таблица 2. Аналитическая группировка

№ группы	Группы организаций по ценам	Число орг-ций	Цена на первичном рынке жилья, тыс. руб./ м2		Прибыль, тыс. руб.
			всего	в среднем	всего	в среднем
1	20,6-23,5	3	64,9	21,63	450	150
2	23,5-26,4	6	146,4	24,4	1800	300
3	26,4-29,3	9	244,5	27,17	3570	396,67
4	29,3-32,2	8	244,5	30,56	4500	562,5
5	32,2-35,2	4	136,4	34,1	3080	770
	Всего	30	836,7	27,89	13400	446,67

Анализ таблицы 2 показывает, что между рассматриваемыми признаками существует прямая корреляционная связь (увеличение цены за 1 м² ведет к увеличению прибыли).  Общая дисперсия (данные таблиц ):

  Таблица 3.Расчет межгрупповой дисперсии

№ группы	Прибыль на 1 организацию, млн. руб.,	Количество организаций fi
1	150,00	3	264033,33
2	300,00	6	129066,67
3	396,67	9	22500,00
4	562,50	8	107338,89
5	770,00	4	418177,78
Итого	446,67	30	941116,67

Межгрупповая дисперсия:

  Коэффициент детерминации:

  Вывод:

прибыль на 87,92% зависит от выручки от цены на первичном рынке жилья, а на 12,08% от неучтенных в модели факторов. Эмпирический коэффициент корреляции:

  Вывод: связь между прибылью и ценой на первичном рынке жилья тесная.

16. Методы оптимизации при принятии решений: сущность и общая характеристика. Линейное и целочисленное программирование. Типовые задачи оптимизации.

Очень распространенными являются оптимизационные задачи. Их цель: поиск оптимального решения в соответствии с целевой функцией при заданных ограничениях. При этом целевая функция является линейной, а ограничения задаются линейными неравенствами.

К методам оптимизации относятся:

1. Линейное программирование.

2. Целочисленное программирование.

3. Теория графов.

Линейное программирование. Наиболее распространены линейные функции, линейные ограничения. Впервые применил Канторович Л.В. в 1930^хгг. Решал задачи производственного менеджмента и оптимизации производства. В США после второй мировой войны. 1975г – Канторович, нобелевская премия по экономике за эти методы.

Модель линейного программирования применяют для определения оптимального способа распределения дефицитных ресурсов при наличии конкурирующих потребностей. Данный вид модели наиболее распространен на промышленных предприятиях. Линейное программирование обычно используют специалисты штабных подразделений для разрешения производственных трудностей. Оно заключается в том, что помогает максимизировать прибыль при наличии одного нескольких ресурсов, каждый из которых используется для производства нескольких видов товара. Обычно при решении оптимизации данного типа моделей обычно используется Симплекс-метод.

Типичные варианты применения линейного программирования в управлении производством:

- Укрупненное планирование производства.

Составление графиков производства, минимизирующих общие издержки с учетом издержек в связи с изменением ставки процента.

- Планирование ассортимента изделий.

Определение оптимального ассортимента продукции, в котором каждому ее виду свойственны свои издержки и потребности в ресурсах.

- Маршрутизация производства изделия.

Определение оптимального технологического маршрута изготовления изделия.

- Управление технологическим процессом.

Сведение к минимуму отходов (стали, ткани, кожи и т.д.).

- Регулирование запасов.

Определение оптимального сочетания продуктов на складе и хранилище.

- Календарное планирование производства.

Составление календарных планов, минимизирующих издержки с учетом расходов на содержание запасов, оплату сверхурочной работы и заказов на стороне.

- Планирование распределения продукции.

Составление оптимального графика отгрузки с учетом распределения продукции между производственными предприятиями и складами, складами и магазинами.

- Распределение рабочих.

Минимизация издержек при распределении рабочих по местам

Типовые задачи линейного программирования:

1. Производственная задача.

2. Двойственная задача.

3. Задача о диете.

4. Транспортная задача.

Методы решения задач линейного программирования и целочисленного программирования различаются. Для линейного программирования используются методы вычислительной математики, а не экономики:

- простой перебор;

- направленный перебор;

- симплекс метод.

Целочисленное программирование. Применяется к решению задач в которых переменные – целые числа.

К ним относятся:

1. задача о выборе оборудования;

2. задача о ранце;

3. задачи размещения (любых объектов);

4. задачи теории расписаний;

5. задачи календарного и оперативного планирования;

6. задачи назначения персонала и др.

Для целочисленного программирования применяют методы:

- метод приближения непрерывными задачами (сначала линейное программирование, потом только целые числа);

- метод направленного перебора (метод ветвей и границ).

Теории графов. Относятся к дискретной математике. Граф – совокупность точек (вершин), которые соединены дугами (ребрами). Исходному объекту приписывают новые качества, например ориентированный граф. В экономике дугам графа приписывают числовые значения (стоимость, время).

Типовые задачи:

- задачи коми-вояжера (посетить все вершины графа и вернуться в исходную вершину с минимальными затратами);

- задача о кратчайшем пути (найти самый короткий путь);

- задача о максимальном потоке (послать максимальное количество груза при ограниченной пропускной способности).

Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи).

Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку). Под названием транспортная задача, определяется широкий круг задач с единой математической моделью, эти задачи относятся к задачам линейного программирования и могут быть решены оптимальным методом. Однако, спец.метод решения транспортной задачи позволяет существенно упростить её решение, поскольку транспортная задача разрабатывалась для минимизации стоимости перевозок.

Классическую транспортную задачу можно решить симплекс-методом, но в силу ряда особенностей её можно решить проще (для задач малой размерности).

Условия задачи располагают в таблице, вписывая в ячейки количество перевозимого груза из   в   груза  , а в маленькие клетки — соответствующие тарифы  .

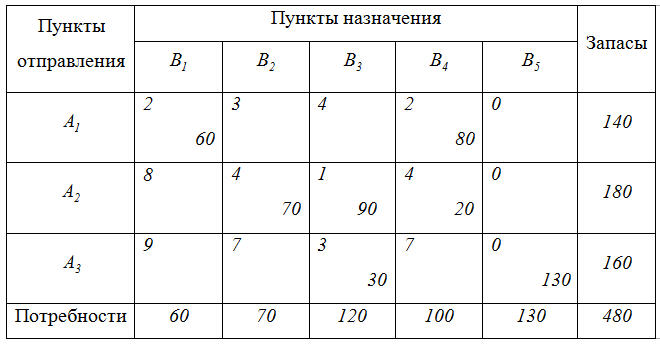
Требуется определить опорный план и путём последовательных операций найти оптимальное решение.