14. Методы прогнозирования и планирования при разработке управленческих решений в условиях риска. Методы стратегического планирования.

Прогнозирование – это составная часть планирования, позволяющая с определенной точностью представить ожидаемый ход развития событий для принятия эффективного управленческого решения.

В теории решений применяется понятие технологическое прогнозирование означающее переход от идеи к конкретному решению проблемы.

Методы изыскательского прогнозирования:

1. Экстраполяция.

2. Моделирование.

3. Метод исторических аналогий.

4. Метод сценариев и др.

Используются точные эмпирические данные и преимущественно количественная информация.

Методы нормативного прогнозирования:

1. Метод Паттерн: обоснование планирования посредством научно-технической оценки количественных данных.

2. Метод Делфи.

3. Методы прогнозного графа Поспелова и Глушкова.

Предпочтение отдается качественной информации.

При разработке прогноза к их числу относятся ситуации, когда данные представлены не только в виде количественных, но и в качественных (словесных) описаний. В связи с этим большое распространение получает экспертное прогнозирование.

Основные этапы разработки прогноза:

1. Подготовка к разработке прогноза (предпрогнозное ориентирование). Определяется прогнозный фон (границы внешней среды).

2. Анализ ретроспективной информации (прошлого), внешних и внутренних условий.

3. Определение наиболее вероятных вариантов развития внешних и внутренних условий (сценарный прогноз).

4. Проведение экспертизы.

5. Разработка альтернативных вариантов действий и решений.

6. Априорная (предварительно) и апостериорная оценка качества прогноза.

7. Контроль хода реализации и корректировка прогноза. Проводится мониторинг.

8. Начало нового цикла прогноза.

Успешность прогнозирования зависит от таких условий:

- объема и качества информации о прогнозируемом процессе, объекте управления;

- правильности формулирования задачи прогнозирования и обоснованности выбора способа ее решения;

- наличия необходимых вычислительных средств и вычислительного аппарата в соответствии с выбранным методом.

Методы (методика) прогнозирования – определенное сочетание приемов (способов) выполнения прогностических операций, получение и обработка информации о будущем на основе однородных методов разработки прогноза.

В 1927 году В.А.Базаров-Руднев предложил 3 метода прогноза: экстраполяция, аналитическая модель, экспертиза.

Современные технологии прогнозирования основаны на использовании различных математических теорий:

- функциональный анализ,

- теория рядов,

- теория экстраполяции и интерполяции,

- теория вероятности,

- математическая статистика,

- теория случайных функций и случайных процессов,

- корреляционный анализ,

- теория распознавания образов.

Для прогнозирования в практической деятельности применяются различные количественные и качественные методы:

1. Количественные методы (приемы) базируются на информации, которую можно получить, зная тенденции изменения параметров или имея статистически достоверные зависимости, характеризующие производственную деятельность объекта управления. Примеры этих методов анализ временных рядов, каузальное (причинно-следственное) моделирование.

2. Качественные методы основаны на экспертных оценках специалистов в области принимаемых решений, например методы экспертных оценок, мнение жюри (усреднение мнений экспертов в релевантных сферах), модели ожидания потребителя (опрос клиентов).

В настоящее время существует около 220 методов прогнозирования, но чаще всего на практике используются не более 10, среди них: 

• фактографические (экстраполяция, интерполяция, тренд-анализ), 

• экспертные (в т.ч. опрос, анкетирование), публикационные (в т.ч. патентные), 

• цитатно-индексные,

• сценарные,

• матричные,

• моделирование, 

• аналогий, 

• построение графов и т.д.

Краткая характеристика методов прогнозирования и область их применения

Метод	Основные условия применения	Особенности приме­нения	Область применения
1 . Сценар­ный (функ­ционально-логическое прогнозиро­вание)	Наличие определен­ного количества ва­риантов развития системы	Подчинение страте­гической функции развития системы, выбор оптимальной альтернативы управ­ления. Установление логической последо­вательности событий	Сценарии разрабатыва­ются для определения рамок будущего разви­тия технологии, рыноч­ных сегментов, стран и регионов и т.д. Долго­срочный прогноз, прак­тически неограничен
2. Экстра­поляция	Количественное оп­ределение важней­ших параметров по­ведения объекта не менее чем за 5 пе­риодов	Прогнозирование на основе предположе­ния о неизменности тенденций в буду­щем	Прогнозирование пока­зателей по предприятию, прогноз потребностей в ресурсах, прогнозирова­ние спроса, финансовое прогнозирование. Крат­косрочный прогноз
3. Регресси­онный ана­лиз	Используется для объектов, имеющих сложную, многофак­торную природу. Предполагает нали­чие выборки по ис­следуемым объектам и показателям	Исследует зависи­мость определенной величины от другой величины или не­скольких величин	Прогнозирование объема инвестиций, уровня за­трат, финансовых ре­зультатов, объемов про­даж и т.п. Используется в среднесрочном прогно­зировании
4. Эксперт­ный	Создание эксперт­ной группы из высо­коквалифицирован­ных специалистов в данной области (численностью не менее 9 человек)	Прогнозирование развития объектов по экспертным оценкам	Прогнозирование рын­ков сбыта, сроков об­новления выпускаемой продукции, прогноз технического уровня продукции. Срок про­гнозирования не огра­ничен
5. Струк­турное про­гнозирова­ние	Возможности реше­ния проблемы при сохранении функ­ций, но изменении структуры и (или) значений парамет­ров объекта	Построение про­гнозных графов и «дерева целей»	Прогноз развития объ­екта в целом, формули­ровка сценария дости­жения прогнозируемой цели. Срок прогнозиро­вания не ограничен
6. Прогно­зирование по аналогии	Используется при схожести объектов прогнозирования, их целей, последствий прогноза	Применяется только для доказанной ана­логии между объек­тами, нельзя приме­нять для новых объ­ектов, процессов, ситуаций, т.е. не имеющих аналогов	Может применяться для установления качест­венной и количествен­ной аналогии с целью изучения опыта, результатов и т.п. Кратко­срочное и среднесроч­ное прогнозирование
7.Комплексные системы прогнозирования (комби­нирован­ный метод)	Условия определен­ные для конкретных методов прогнозиро­вания (п.п. 1-6)	Возможность рацио­нального сочетания методов с целью по­вышения точности прогнозирования, снижения затрат на прогнозировании	Для всех видов прогно­зирования. Срок не ог­раничен

Появляются новые методы:

- адаптивные методы прогнозирования – построение самонастраивающихся рекуррентных моделей, способных отражать изменяющиеся во времени динамические свойства временного ряда и учитывать информационную ценность его членов;

- морфологическое исследование (для систематического и непредубежденного отбора возможностей в связи с изыскательским прогнозированием);

- ретроальтернативистика (И.В. Бестужев-Лада);

- метод «дерево целей» (впервые использован при разработке схемы ПАТТЕРН) для нормативного прогнозирования и оценки «общих элементов»;

- «контекстуальное картографирование» (contextual mapping);

- причинно-следственный метод, близкий к проблемно-целевому методу (Базарова-Руднева);

- комбинированный прогноз – некоторая обобщающая оценка, получаемая на основе формального или неформального объединения частных прогнозов, чаще всего путем суммирования их с определенными весовыми коэффициентами.

Однако чаще всего анализ опирается на разработанные в начале и середине 20 века статистические методы:

• временной и пространственной экстраполяции;

• корреляционные, регрессионные и факторные;

• эконометрические и эвристические;

• моделирования процессов развития.

Рассмотрим подробнее самые распространенные методы прогнозирования.

Экстраполяция представляет собой процедуру переноса ранее сделанных выводов по поводу какой-то части объектов, явлений и закономерностей за пределы известного на все множество этих объектов, явлений или закономерностей.

Экстраполяция – это метод прогнозирования, построенный на основании ранее полученных и изученных данных, предположения с видом на будущее. Причем прогноз этим методом может составляться как на количественные характеристики, так и на качественные.

Данный метод позволяет работать с «неизвестными» на основании полученных знаний, предполагает работу с «будущим», исходя из достоверной информации о прошлом и настоящем. Он применяется, например, при расчете смертности или роста рождаемости населения. Основаниями служат объективные факторы прошлых лет и настоящего времени, которые оказались наиболее влияющими на эти показатели.

В экономике метод экстраполяции является одним из самых действенных в плане прогнозирования динамики социально-экономических явлений. С его помощью можно составить прогноз конъюнктуры товарного рынка. За основу расчетов здесь берутся данные изучения и анализа, определяющие степень развития и тенденции развития международной торговли и производства в перспективе.

Данный метод прекрасно подходит для определения будущих показателей объема рынка, величины складских запасов, но его прогнозы могут казаться неверными в вопросе определения уровня продаж, так как не учитывает возможность возникновения неожиданных факторов, которые существенно могут повлиять на прежний ход вещей. На основании экстраполяции можно с точностью до 75 % дать прогноз на завтрашний день, но вероятность его точности на месяц уже может упасть до 30%, так как не учитываются неожиданные факторы влияния.

Если проводить экстраполяцию в будущее – она будет называться перспективной, а если в прошлое – ретроспективной.

Применение экстраполяции основано на двух основных предпосылках:

• дальнейшее развитие исследуемого явления описывается плавной кривой;

• общая тенденция развития того или иного явления в настоящем или прошлом не должна претерпевать значительных изменений в обозримом будущем.

Применение экстраполяции целесообразно в начальной стадии построения точных окончательных прогнозов. Механическое использование этого метода способно привести к серьезным погрешностям, что может стать причиной неправильных выводов и неточных исследований. Для того чтобы результаты прогнозирования были максимально точными, следует учитывать все возможные гипотезы, предпосылки и условия.

Прогнозную экстраполяцию можно разбить на два этапа.

1) Выбор оптимального вида функции, описывающей ретроспектив­ный ряд данных. Выбору математической функции для описания тренда предшествует преобразование исходных данных с использованием сгла­живания и аналитического выравнивания динамического ряда.

2) Расчет коэффициентов (параметров) функции, выбранной для экст­раполяции.

К методам экстраполяции относятся:

- метод скользящих средних,

- метод экспоненциального сглаживания;

-метод наименьших квадратов.

Методы (приемы) экстраполяции:

1. Экстраполяция на основе среднего коэффициента роста (метод скользящих средних). Применяется, когда имеет место резкое колебание показателей по годам наблюдения и не обнаруживается тенденция к росту или снижению показателей. Метод позволяет отвлечься от случайных колебаний временного ряда. Это достигается путем замены значений внутри выбранного интервала средней арифметической величиной. Интервал, величина которого остается постоянной, постепенно сдвигается на одно наблюдение. Величина интервала скольжения –Р– может принимать любое значение от минимального (Р = 2) до максимального (Р = N – 1, где N — длина рассматриваемого временного ряда). Сглаженный ряд короче первоначального.

2. Экстраполяция на основе экспоненциального сглаживания. Позволяет построить такое описание процесса (динамического ряда), при котором более поздним наблюдениям придается большее значение по сравнению с ранними наблюдениями, причем важность значении наблюдений на ранних этапах убывает по экспоненте, тогда как экстраполяция методом подбора функций учитывает все данные исходного динамического ряда с одинаковым "весом".

Общий вид экспоненциального уравнения регрессии:

y=aebx или y=ea+bx .

Для упрощения алгоритма обработки выборочной совокупности проводится линеаризация экспоненциального уравнения регрессии путем логарифмирования второго из представленных  уравнений

ln y=a+bx.

 Проведя замену ln y на z, получается линейное уравнение вида:

z=a+bx.

Далее используя систему нормальных уравнений для линейной зависимости

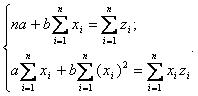
Определяем параметры уравнения регрессии  a и b. Производя обратную замену,  получаем эмпирические значения результирующего признака.

3. Экстраполяция на основе метода наименьших квадратов (МНК) (метода подбора функций, аналитического выравнивания динамических рядов).  Метод основан на методе математической экстраполяции, которая в математическом смысле означает распространение закона изменения функции из области ее наблюдения на область, лежащую вне отрезка наблюдения. Суть метода - в выборе оптимального вида функции (прямая, парабола, гипербола, логарифмическая, их комбинированное сочетание), которая наиболее точно описывает тенденцию изменений объекта прогнозирования в будущем.

Суть названия «метода наименьших квадратов» (МНК) в том, что выравнивающая функция (прямая, гипербола, парабола, др.) будет занимать такое положение среди точек фактических значении показателей, при котором суммарное отклонение точек от функции будет минимальным, т.е. искомые параметры должны удовлетворять условию:

где S – выравнивающая функция (линейная функция (прямая), гипербола, парабола и др.)

y_i – фактические уровни показателей в динамическом ряду

y¢_i – расчетный ряд прогнозируемых показателей, вычисленный по уравнению функции;

n – число наблюдений

Задача выбора функции заключается объективно отразить изменяющие тенденции в объекте прогнозирования, и определении лучшей формы связей (коэффициент корреляции) между прогнозируемым фактором и факторами-признаками влияющими на него.

По выбору формы кривой определяют прогноз на среднесрочную перспективу. Для выбора кривой используют как простые функции типа:

- прямой у = а + bх (линейная функция),

- гиперболы y = a + b/x,

- параболы: у = а + bх + сх² и др.,

так и сложные, комбинированные функции, сочетание выше названных функции. Например, y = a + blnt + ct и др.

Метод применяется при среднесрочном прогнозировании, на начальном этапе для выявления тенденций присущих объекту прогнозирования.

Исходной информацией для экстраполяции с помощью метода подбора функций являются временные (динамические) ряды.

Временной ряд представляет собой упорядоченные во времени наборы измерений тех или иных характеристик исследуемого объекта, т.е. множество наблюдений, полученных последовательно во времени.

Этапы реализации метода подбора функций:

I этап. Сбор информации за ряд лет о прошлом объекта прогнозирования и представления ее в виде динамического ряда.

II этап. Построение графика о функционировании объекта прогнозирования в прошлом до настоящего периода. По виду построенного графика устанавливают: имеет ли исследуемый динамический ряд прогнозируемого объекта (урожайность) отчетливо выраженную тенденцию к росту или снижению, если да, то является ли она плавной и какой характер тенденции (монотонная или немонотонная, возрастающая или убывающая).

Выбор функции, которая наиболее реально отражает изменения в объекте прогнозирования, проводится с помощью метода наименьших квадратов.

Прямолинейная зависимость имеет вид:

Парабола второй степени при b > 0 и с < 0 симметрична относительно точки максимума, изменяю­щей направление связи, а именно рост на падение.

Такого рода функцию можно наблюдать в экономике труда при изучении зависимости заработной платы работников физического труда от возраста, с увеличением возраста повышается заработная плата ввиду одновременного увеличения опыта и повышения квалификации работника. Однако с определенного возраста ввиду старения организма и снижения производительности труда дальнейшее повышение возраста может приводить к снижению заработной платы работника.

Гиперболическая зависимость:

Может быть использована на микро- и макроуровне - например, для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота. Классическим ее примером является кривая Филлипса, характеризующая соотношение между нормой безработицы и процентом прироста заработной платы.

III этап. Расчет коэффициентов (параметров) функции, выбранной для экст­раполяции.

1. Линейная модель (модели зависимости Y от Х ) имеет вид:

y_x=a+b*x.

При этом b называют коэффициентом регрессии; a называют свободным членом уравнения регрессии.

Система нормальных уравнений:

 у = na + b х;

 ху = а х + b x² .

Коэффициенты находятся по формулам:

 у  х² - xу х

a = -----------------------;

n x² -  х x

n xу - x y

b = -----------------------.

n x² -  х x

Если в решаемой задаче много цифр, то:

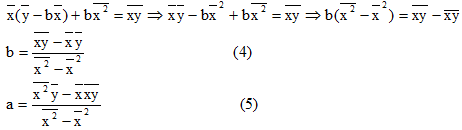
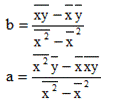align=absMiddle v:shapes="_x0000_i1051">

Полученная прямая является оценкой для теоретической линии регрессии. Имеем:

Итак,   является уравнением линейной регрессии.

2. Уравнение регрессии параболы 2-го порядка имеет следующий вид:

y=a+bx+cx²

 Нормальные уравнения метода наименьших квадратов для параболической зависимости таковы:

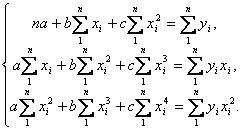
Решая эту систему уравнений, получаем значения параметров a, b и c.

3. Уравнение регрессии гиперболы имеет следующий вид:

Из системы нормальных уравнений метода наименьших квадратов для гиперболы:

определяются значения коэффициентов гиперболического уравнения регрессии a и b.

4. Степенная форма зависимости (логарифмическая).

Общий вид степенного уравнения регрессии:

y=a·xb.

Логарифмирование дан­ного уравнения приводит его к линейному виду:

ln y = ln a + b ln x

Оценки параметров a и b уравнения могут быть найдены МНК. Система нормальных уравнений имеет вид:

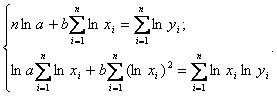
Параметр b определяется из системы, а параметр a – потенцированием выражения lna.

IV этап. Оценка достоверности прогнозных расчетов. Проводят с помощью приемов математической статистики и графиков.

- Индекс детерминации R²  используется для проверки статистической значимости в целом уравнения нелинейной регрессии по F-критерию Фишера:

,

где m – число параметров при переменных х; n – число наблюдений.

Если Fфакт>Fкрит(α; m; n - m - 2) , то гипотеза Н0 о статистической не значимости  уравнения регрессии отклоняется.

Для степенной функции yx=axb,  гиперболы  , экспоненты y=ea+bx формула F-критерия имеет вид:

.

Для параболы второй степени y=a+bx+cx2:

.

- Индекс корреляции (показатель тесноты нелинейной корреляции), вычисляемый по формуле:

                                      ,                                            

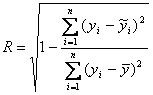где ỹi - индивидуальные значения у  по уравнению связи.

Индекс корреляции находится в границах: 0 < R < 1 и чем ближе к единице, тем теснее связь рассматриваемых признаков, более надежно найденное уравнение регрессии.

Пример №1. Прогноз на основе линейной регрессии.

На основании нижеследующих данных о продажах и расходах на рекламу (графы 2 и 3) составить прогноз ожидаемого объема продаж в будущем периоде (при расходах на рекламу в 20 тыс. руб.):

Таблица 1. Таблица исходных расчетных значений

Периоды	Расходы на рекламу, тыс. руб., х	Продажи, млн. руб., у	х * у	х2	у2
1	2	3	4	5	6
1	18	30	540	324	90
2	38	40	1520	1444	1600
3	22	28	616	484	784
4	28	32	896	784	1024
5	46	50	2300	2116	2500
6	24	40	960	576	1600
7	24	40	960	576	1600
8	44	46	2024	1936	2116
9	14	28	392	196	784
10	26	44	1144	676	1936
11	30	36	1080	900	1296
12	34	36	1224	1156	1296
	å х =348	å у = 450	å ху =13656	å х2 = 11168	å у2 =17436

Решение:

1. рассчитываем значение b (для чего предварительно составляем таблицу значений):

Пример №2. Три метода экстраполяции.

Таблица 1. – Исходные данные

Год	N п/п	Трансфертные платежи, млн. долларов
2001	1	189,1
2002	2	230,8
2003	3	255,1
2004	4	274,8
2005	5	299,4
2006	6	334,5
2007	7	394
2008	8	453
2009	9	505
2010	10	552
2011	11	593
2012	12	644
2013	13	683
2014	14	715
2015	15	768

Задание: рассчитать точечный прогноз на 2022-ой год, используя приемы экстраполяции:

1 Экстраполяция на основе среднего коэффициента роста.

2 Экстраполяция на основе экспоненциального сглаживания.

3 Экстраполяция на основе метода наименьших квадратов.

Выбрать наиболее вероятный прогноз.

1 Экстраполяция на основе среднего коэффициента роста . В основу расчета положен средний темп роста.

Прогнозируемый результат определяется по формуле:   где У_баз. – базовый уровень, принятый за основу экстраполяции (за начальную точку экстраполяции); - средний коэффициент роста; l – дальность прогнозирования (период упреждения). В качестве базового принимается последний уровень исходного ряда.

Средний коэффициент роста рассчитывается по формуле, как среднее арифметическое коэффициентов, рассчитанных по каждому году.

где К_i - темпы роста, рассчитанные по каждому году.

Для этого необходимо рассчитать коэффициенты роста за каждый период на основе динамики исходного ряда по формуле:

Коэффициент роста в текущем году равен отношению показателя данного года к предыдущему значению.

Расчет коэффициентов представлен в таблице 2.

Таблица 2 – Расчет коэффициентов роста.

Годы	Уф	Кi
1	189,1	-
2	230,8	1,2205182
3	255,1	1,105286
4	274,8	1,0772246
5	299,4	1,0895197
6	334,5	1,1172345
7	394	1,1778774
8	453	1,1497462
9	505	1,1147903
10	552	1,0930693
11	593	1,0742754
12	644	1,0860034
13	683	1,060559
14	715	1,0468521
15	768	1,0741259
Сумма		15,487082

Средний коэффициент роста составит: name=object6 align=absmiddle v:shapes="_x0000_i1029">. Рассчитаем прогноз: У₁₆ = 768 ∙ 1,1062 = 849,6 У ₁₇ = 768 ∙ 1,1062 ² = 939,8 У ₁₈ = 768 ∙ 1,1062 ³ = 1039,6 У ₁₉ = 768 ∙ 1,1062 ⁴ = 1150 У ₂₀ = 768 ∙ 1,1062 ⁵ = 1272,1 У ₂₁ = 768 ∙ 1,1062 ⁶ = 1407,2 У ₂₂ = 768 ∙ 1,1062 ⁷ = 1556,7

Вывод: по среднему коэффициенту роста трансфертные платежи в 22-м году составят 1556,7 млн.долл.

2. Экстраполяция на основе экспоненциального сглаживания. Экстраполяция на основе экспоненциального сглаживания осуществляется по формуле:

S_t = α ∙ X_t + (1 - α) ∙ S_t-1 , (2.6)

где S_t – текущее сглаженное значение; Х_t – текущее значение исходного ряда; S_{t – 1} – предыдущее сглаженное значение; α - сглаживающая const. α = 0…1 – необходимо выбрать наиболее приемлемое значение с тем, чтобы сглаженный ряд в наибольшей степени отражал закономерность развития, был приближен к динамике исходного ряда и позволял усреднить базовый уровень. α = 0,5.

Таблица 3 – Экспоненциальное сглаживание

Год	Трансфертные платежи, млн. долларов	Экспоненциальное сглаживание
1	189,1	189,1
2	230,8	209,95
3	255,1	232,53
4	274,8	253,66
5	299,4	276,53
6	334,5	305,52
7	394	349,76
8	453	401,38
9	505	453,19
10	552	502,59
11	593	547,8
12	644	595,9
13	683	639,45
14	715	677,22
15	768	722,61

S₁ = 189,1. S₂ = 0,5∙ 230,8 + (1-0,5) ∙ 189,1 = 209,95. S₃ = 0,5∙ 255,1 + (1-0,5) ∙ 209,95= 232,53. S₄ = 0,5∙ 274,8 + (1-0,5) ∙ 232,53= 253,66 S₅ = 0,5∙ 299,4 + (1-0,5) ∙ 253,66= 276,53 S₆ = 0,5∙ 334,5 + (1-0,5) ∙ 276,53= 305,52 S₇ = 0,5∙ 394 + (1-0,5) ∙ 305,52= 349,76 S₈ = 0,5∙ 453 + (1-0,5) ∙ 349,76= 401,38 S₉ = 0,5∙ 505 + (1-0,5) ∙ 401,38= 453,19 S₁₀ = 0,5∙ 552 + (1-0,5) ∙ 453,19= 502,59 S₁₁ = 0,5∙ 593 + (1-0,5) ∙ 502,59= 547,8 S₁₂ = 0,5∙ 644 + (1-0,5) ∙ 547,8= 595,9 S₁₃ = 0,5∙ 683 + (1-0,5) ∙ 595,9= 639,45 S₁₄ = 0,5∙ 715 + (1-0,5) ∙ 639,45= 677,22 S₁₅ = 0,5∙ 768 + (1-0,5) ∙ 677,22= 722,61 На основании полученного ряда рассчитывается средний коэффициент роста, аналогично предыдущему методу. 

Таблица 4 – Средний коэффициент роста после экспоненциального сглаживания

Годы	Уф	Кi
1	189,1	-
2	209,95	1,1103
3	232,53	1,1075
4	253,66	1,0909
5	276,53	1,0902
6	305,52	1,1048
7	349,76	1,1448
8	401,38	1,1476
9	453,19	1,1291
10	502,59	1,109
11	547,8	1,09
12	595,9	1,0878
13	639,45	1,0731
14	677,22	1,0591
15	722,61	1,067
Сумма		15,4111

, (2.8) где К_i – коэффициенты роста, рассчитанные по экспоненциальному ряду; m – число точек в экспоненциальном ряду. Тогда прогноз рассчитывается аналогично предыдущему методу: , (2.9) где У_{баз.эксп.} – последнее значение выбранного экспоненциального ряда. У₁₆ = 722,61 ∙ 1,1008 = 795,45 У ₁₇ = 722,61 ∙ 1,1008 ² = 878,63 У ₁₈ = 722,61 ∙ 1,1008 ³ = 963,89 У ₁₉ = 722,61 ∙ 1,1008 ⁴ = 1061,05 У ₂₀ = 722,61 ∙ 1,1008 ⁵ = 1168,01 У ₂₁ = 722,61 ∙ 1,1008 ⁶ = 1285,74 У ₂₂ = 722,61 ∙ 1,1008 ⁷ = 1415,35

Вывод: по методу экспоненциального сглаживания трансфертные платежи в 22-м году составят 1415,35 млн.долл.

3. Прогноз на основе метода наименьших квадратов. Для начала нужно выбрать функцию

Критерием правильности выбора функции является минимум суммы расчетных значений показателя от фактических: S = ∑ (Уф - Ур)² min.

Так как сумма квадратов отклонений расчетных значений показателя от фактических у функции параболы меньше, чем у прямой, то для прогнозирования наиболее приемлема функция параболы.

Произведем расчеты на основе функции параболы. Система нормальных уравнений для функции параболы имеет вид: A∙ n + B∙∑ t + C∙∑ t² = ∑ У;  A∙∑ t + B∙∑ t² + C∙∑ t³ = ∑ У∙ t; A∙∑ t² + B∙∑ t³ + C∙∑ t⁴ = ∑ У∙ t².

Для упрощения расчетов присвоим t такие значения, чтобы ∑ t = 0. Тогда система уравнений примет вид: A∙ n + + C∙∑ t² = ∑ У;  B∙∑ t² + = ∑ У∙ t; A∙∑ t² + C∙∑ t⁴ = ∑ У∙ t².

Для составления системы уравнений для функции параболы выполним расчеты по форме таблицы 5.

Таблица 5 – Сводная таблица для функции параболы.

Год	Уфакт	t	t2	t4	У t	У t2	Урасч	(Уф - Ур)	(Уф - Ур)2
1	189,1	-7	49	2401	-1324	9265,9	181,1	8	63,915
2	230,8	-6	36	1296	-1385	8308,8	214,6	16,2	260,91
3	255,1	-5	25	625	-1276	6377,5	249,6	5,5	30,003
4	274,8	-4	16	256	-1099	4396,8	286	-11,2	126,14
5	299,4	-3	9	81	-898,2	2694,6	323,9	-24,5	598,94
6	334,5	-2	4	16	-669	1338	363,1	-28,6	820,75
7	394	-1	1	1	-394	394	403,9	-9,9	97,174
8	453	0	0	0	0	0	446	7	49
9	505	1	1	1	505	505	489,6	15,4	237,91
10	552	2	4	16	1104	2208	534,6	17,4	303,29
11	593	3	9	81	1779	5337	581	12	143,35
12	644	4	16	256	2576	10304	628,9	15,1	227,91
13	683	5	25	625	3415	17075	678,2	4,8	22,92
14	715	6	36	1296	4290	25740	729	-14	194,75
15	768	7	49	2401	5376	37632	781,1	-13,1	172,43
итог	6890,7	0	280	9352	12001	131577	6890,7	0	3349,4

Используя значения таблицы 5, составим систему уравнений: A∙ 15 + C∙280 = 6890,7; B∙280 = 12001; A∙280 + C∙9352 = 131577.

В  = 12001/280; А = 459,38-18,7 ∙ С; С= (459,38-18,7 ∙ С) ∙ 280 + 9352 ∙ С = 131577

Решив систему уравнений, получим значения параметров: А =446; В = 42,859; С =0,7167. Следовательно, уравнение параболы в нашем примере имеет вид: У_расч = 446 + 42,859 ∙ t + 0,7167 ∙ t² .

Выполним аналогичные расчеты на основе функции прямой. Уравнение прямой: A∙ n + B∙∑1/ t = ∑ У; A∙∑ t + B∙∑ t² = ∑ У∙ t.

Таблица 6 – Сводная таблица для функции прямой.

Год	Уфакт	t	t2	У t	Урасч	(Уф - Ур)	(Уф - Ур)2
1	189,1	-7	49	-1324	159,36	29,74	884,47
2	230,8	-6	36	-1385	202,22	28,58	816,82
3	255,1	-5	25	-1276	245,08	10,02	100,4
4	274,8	-4	16	-1099	287,94	-13,14	172,66
5	299,4	-3	9	-898,2	330,8	-31,4	985,96
6	334,5	-2	4	-669	373,66	-39,16	1533,5
7	394	-1	1	-394	416,52	-22,52	507,15
8	453	0	0	0	459,38	-6,38	40,704
9	505	1	1	505	502,24	2,76	7,6176
10	552	2	4	1104	545,1	6,9	47,61
11	593	3	9	1779	587,96	5,04	25,402
12	644	4	16	2576	630,82	13,18	173,71
13	683	5	25	3415	673,68	9,32	86,862
14	715	6	36	4290	716,54	-1,54	2,3716
15	768	7	49	5376	759,4	8,6	73,96
итог	6890,7	0	280	12001	6890,7	0	5459,2

A ∙15 =6890,7; B∙280 =12001

A= 6890,7/15; В = 12001/280

А = 459,38

В = 42,86 Уравнение прямой имеет вид: У _расч = 459,38+42,86* t. Подставляя в полученное уравнение, значения t из таблицы 6, получим расчетные значения У. 

Рассчитаем прогноз на 22-ой год, исходя из полученного уравнения параболы: У_расч = 446 + 42,859 ∙ t + 0,7167 ∙ t² У₁₆ =446+42,859*8+ 0,7167 *64 =834,7 ; У ₁₇ = 446+42, 859*9+ 0,7167 *81 = 889,8; У ₁₈ = 446+42, 859*10+ 0,7167 *100 = 946,3; У ₁₉ = 446+42, 859*11+ 0,7167 *121 = 1004,2; У ₂₀ = 446+42, 859*12+ 0,7167 *144 = 1063,5; У ₂₁ = 446+42, 859*13+ 0,7167 *169 = 1124,3; У ₂₂ = 446+42, 859*14+ 0,7167 *196 = 1186,5

Вывод: по методу наименьших квадратов (функция параболы) трансфертные платежи в 22-м году составят 1186,5 млн.долл.

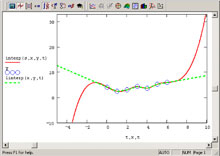
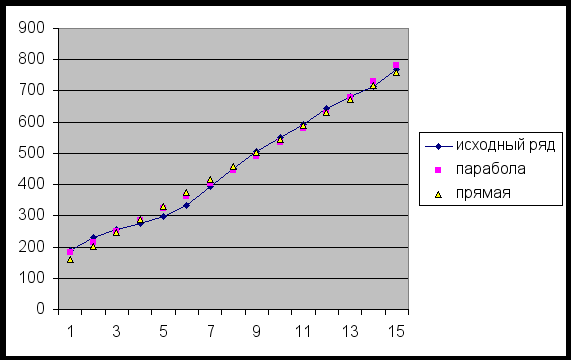
Полученные три прогноза отразим на графике: 

Выбор наиболее вероятного прогноза. Прогноз при помощи среднего коэффициента роста завышен, поскольку за базовый уровень принимается последнее значение исходного ряда. 

Метод экспоненциального сглаживания позволяет построить такое описание процесса, при котором характеризуется не средний уровень процесса, а тенденция, сложившаяся к моменту последнего наблюдения.

Метод наименьших квадратов - прогноз на весь период упреждения будет рассчитываться на основе выбранной функции, несмотря на происходящие изменения. Если расчетные значения У близки или совпадают с фактическими значениями исходного ряда, то можно утверждать, что нам удалось подобрать математическую функцию, соответствующую динамике исходного ряда. Только в этом случае можно говорить о вероятности полученного прогноза.

Таким образом, наиболее достоверным представляется прогноз на основе экспоненциального сглаживания. То есть, трансфертные платежи в 22-м году скорее всего составят 1415,35 млн.долл.

Моделирование в прогнозировании. Инструмент позволяет строить и изучать сценарии изменения интересующих показателей при помощи методов статистического, эконометрического, математического моделирования и визуализировать полученные результаты.

Основные возможности:

• поддержка широкого класса методов моделирования, в том числе эконометрических, балансовых, оптимизационных;

• сценарное прогнозирование возможных последствий принятия управленческих решений («Что будет, если ..?»);

• поиск оптимальных управляющих параметров экономической системы при заданных ограничениях.

Простая трендовая модель динамики - это уравнение тренда с указанием начала отсчета единиц времени. Прогноз по этой модели заключается в подстановке в уравнение тренда номера периода, который прогнозируется.

Модель временного ряда в общем виде описывается следующим выражением:

W( )t =T( )t + N( )t +S( )t +A(t),

где T(t) – тренд, основная составляющая; N(t) – регулярные колебания около тренда; S(t) – сезонная составляющая; A(t) – случайная составляющая (аддитивная помеха).

Например, тренд урожайно­сти зерновых культур во Франции имеет вид: '

Прогноз по этому тренду на 2000 г., номер которого от 1983 г. равен 17, составит:

Интерпретация этого прогноза должна быть следующей: если урожайность зерновых во Франции будет возрастать до 2000 г. с той же средней скоростью (среднегодовым приростом), с какой она росла в период с 1970 по 1995 г., то тренд урожай­ности в среднем пройдет в 2000 г. через точку 75,93 ц/га. Такой прогноз и называется точечным прогнозом.  Поскольку мы дали прогноз с двумя знаками за запятой, то реально это уже не строго точечный прогноз, а прогноз по­падания тренда в интервал от 75,9250001 до 75,9349999 ц/га, т.е. в интервал шириной 0,01 ц/га.

Прогнозирование на один шаг вперед можно вести на основе регрессионной модели по методу наименьших квадратов (МНК).

Для моделирования различных процессов применяется метод Монте-Карло, основанный на использовании случайных чисел. Обобщенный алгоритм реализации метода Монте-Карло обеспечивает прогнозирование работы объекта и вычисление статистических характеристик его функциональных параметров.

В последнее время значительный интерес проявляется к методам, основанным на нелинейных моделях. Большая часть таких методов принадлежит к разряду технологий искусственного интеллекта (ИИ). Это, в первую очередь, искусственные нейронные сети (ИНС) и новейшие средства оптимизации, к числу которых относятся, например, генетические алгоритмы, метод моделирования отжига и другие.

Методы планирования. Прогнозирование – составная часть планирования.

Планирование — оптимальное распределение ресурсов для достижения поставленных целей, деятельность (совокупность процессов), связанных с постановкой целей (задач) и действий в будущем.

Планирование в самом общем виде подразумевает выполнение следующих этапов:

• Постановка целей и задач

• Составление программы действий (проектирования)

• Вариантное составление программы (вариантное проектирование)

• Выявление необходимых ресурсов и их источников

• Определение непосредственных исполнителей и доведение планов до них

• Фиксация результатов планирования в материальном виде, например, в виде проекта, карты боевых действий, приказа в письменной форме и т. п.

Планы являются средством координации деятельности различных подразделений при принятии управленческих решений. В планах определяются имеющиеся ресурсы, необходимые для достижения намеченных целей в рамках конкретного периода. Планы охватывают деятельность производственных отделений, поэтому принятие управленческих решений осуществляется в рамках своих планов. 

Методы планирования.