23. Особенности диффузии донорных примесей.

Диффузия мышьяка:

П 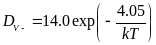реобладающий механизм диффузии – вакансионный. Основной вклад в диффузию мышьяка вносят 2 типа пар мышьяк - вакансия. Это пары, состоящие из замещающего атома мышьяка, т.е. As⁺ и вакансии, нейтральной V⁰ или однократно отрицательно заряженной V^-.

При высоких концентрациях имеет место кластеризация мышьяка.

Наиболее распространенная модель предполагает, что мышьяк образует кластеры по 3 атома и 1 электрону. Атомы кластера положительно заряжены при высоких температурах, но при комнатной температуре кластер, в целом, нейтрален.

3As⁺ + e^- = As₃⁺² => 300^˚K=> As₃

Влияние кластеризации на электрические характеристики: N_ОБЩ = N_А + N_КЛ = N_А + 3M_КЛ, где M_КЛ – концентрация кластеров. Концентрация свободных носителей при высоких температурах: n = N_А + (2/3) N_КЛ = N_А + 2 М_КЛ; при комнатной температуре: n = N_А

Диффузия фосфора:

В диффузии фосфора участвуют и междоузлия, и вакансии. Основной вклад в диффузию фосфора вносят 3 типа пар. Это пары, состоящие из замещающего атома фосфора, т.е. P⁺ и междоузлия, нейтрального I⁰ или акцепторного, однократно ионизованного I^-, или двукратно ионизованной акцепторной вакансии V⁼.

П онятие Е – центров: Е – центр – пара вакансия-примесный атом, которая может быть в различных зарядовых состояниях: Е⁰ – нейтральном; Е^- - акцепторном; Е⁺ - донорном. Модель Файера – Цая для диффузии фосфора предполагает участие акцепторных Е^- - центров. Уравнение образования акцепторных Е^- - центров: Р⁺ + V⁼ = (PV)^-;

DP=

24. Совместная диффузия примесей.

При совместной диффузии обнаружено влияние примесей друг на друга.

Примесь, диффундирующая с высокой концентрацией, оказывает заметное влияние на примесь с низкой концентрацией, тогда как обратное влияние пренебрежимо мало.

Совместная диффузия фосфора и бора:

Ускорение диффузии бора в присутствии фосфора проявляется в биполярных транзисторах с фосфорным эмиттером, как dip-эффект - выдавливание базы под эмиттером.

У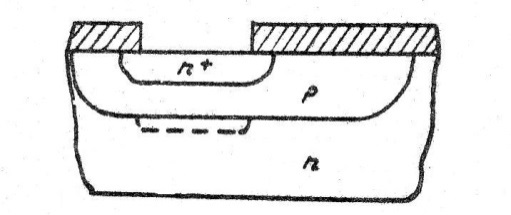 скорение диффузии связано с диссоциацией E – центров в области низких концентраций и увеличением за счет этого концентрации вакансий, что приводит к увеличению коэффициента диффузии бора.

Глубина выдавливания:

Где D_B - собственный коэффициент диффузии бора и D_nB - коэффициент диффузии под эмиттером;

w₀ – глубина базового слоя, t – время диффузии эмиттера.

Совместная диффузия мышьяка и бора:

При совместной диффузии мышьяка и бора глубина базы под эмиттером уменьшается

С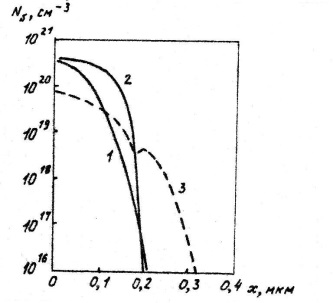 овместная диффузия бора и мышьяка: 1 – распределение бора в начальный момент; 2 – распределение мышьяка в результате диффузии при 1000 ˚С в течение 25 мин.; 3 – распределение бора после диффузии мышьяка. В области подложки наблюдается горб, вызванный притягиванием бора к области p-n перехода. В результате глубина проникновения бора в подложку и, соответственно, глубина базы немного уменьшается.

Совместная диффузия мышьяка и фосфора:

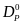
Т радиционно для создания мелкозалегающих исток/стоковых областей n⁺ - типа используется мышьяк, который имплантируется в подложку с неоднородным распределением бора, возникающим в результате подлегирования канала и формирования т. наз. P – кармана. В процессе, разработанным для японского варианта КМДП - технологии уровня 130 нм, для создания n⁺ - областей кроме мышьяка использовалась имплантация фосфора с целью подавления токов утечки. При этом обнаружилось аномальное поведение фосфора в присутствии мышьяка. Бор сегрегирует в хвосте распределения мышьяка, собираясь туда из объема подложки. Пик фосфора возникает за счет ухода примеси из приповерхностной части подложки. При длительном отжиге в хвосте распределения мышьяка создается обедненная фосфором область. Неплохие результаты моделирования рассмотренного аномального эффекта получаются, если предположить, что диффузия в этом случае идет с участием нейтральных и отрицательно заряженных междоузлий, т.е. диффундируют пары (PI)⁺ и (PI)⁰, соответственно. Коэффициент диффузии с учетом весового коэффициента f₀ (оптимально при f₀ = 0.1) можно записать:

- коэффициент диффузии с участием нейтральных междоузлий . - коэффициент диффузии с участием отрицательно заряженных междоузлий, - собственный коэф. диффузии фосфора.

?25. Особенности процесса постимплантационной диффузии. TED-эффект.

С уменьшением размеров требуются все более мелкие области с все более низким сопротивлением. Создание таких слоев без введения дефектов в кремний и без влияния материалов других слоев почти невозможно. В процессе ионной имплантации создается большое число дефектов в подложке, что сильно влияет на процесс постимплантационного отжига. Высокие дозы имплантации приводят к аморфизации поверхности кремния и формированию распределенных дефектов, т.е. дислокаций.

Экспериментально обнаружено, что существует временной интервал, в процессе постимплантационного отжига, когда диффузия идет с существенно более высокой скоростью, примерно постоянной в течение этого интервала. Затем скорость диффузии падает до обычного значения. Этот эффект получил название эффект временно-ускоренной диффузии или TED-эффект. Длительность интервала временно-ускоренной диффузии падает c ростом температуры отжига. Таким образом, при исследовании быстрого постимплантационного отжига: при более высокой температуре отжига могут наблюдаться меньшие глубины p-n переходов. TED-эффект объясняется ускорением диффузии за счет неравновесной концентрации междоузлий, которые отжигаются более быстро при высокой температуре.

Модели, задействованные при расчете TED-эффекта:

- Постимплантационные дефекты +1 модель - Имплантирумый атом создает траекторию разрушений, соударяясь с атомами решетки и смещая их, создавая междоузлия и вакансии. Каждый имплантированный ион может создавать порядка 100 междоузлий (I) и вакансий (V), прежде чем он остановится. Считается, что, хотя полное количество постимплантационных дефектов значительно выше, каждый ион в результате имплантации смещает в среднем 1 атом из решетки, причем распределение междоузлий смещено в глубину подложки, а вакансий - к поверхности.

- Кольца дислокаций - Для случая аморфизирующей имплантации известно о формировании протяженных дефектов на границе между аморфизированной и кристаллической областями. Эти протяженные дефекты известны как кольца дислокаций.

При моделировании дислокационные кольца считаются имеющими одинаковый радиус и плотность и оцениваются по результатам исследований с помощью просвечивающей электронной микроскопии. Расположение колец определяется по глубине аморфного слоя.

- Кластеризация точечных дефектов - Согласно экспериментальным исследованиям междоузлия группируются в плоскости {113}. Найдено, что эти кластеры диссоциируют во время отжига и скорость диссоциации экспоненциально падает. Поэтому за короткое время только часть имплантированных дефектов способна внести вклад в TED-эффект.

Если время увеличивается, то число высвобождаемых дефектов возрастает, и вклад в TED – эффект увеличивается. Если отжиг идет при высокой температуре, большинство кластеров активно диссоциируют в процессе роста температуры. Поэтому должен быть произведен тщательный учет диссоциации кластеров при моделировании подъема температуры в процессе отжига