7. Системы координат при моделировании ионной имплантации.

Первая система координат – это система, привязанная к реальной установке ионной имплантации. В этой системе координат ионный пучок всегда направлен вдоль оси –Z.

Вторая система координат – это система, привязанная к подложке. В этой системе всегда ось X направлена вдоль базового среза пластины, ось Z – перпендикулярно поверхности подложки. Ось Y образует с заданными осями X и Z правую тройку

Третья система координат – это система, построенная непосредственно для проведения вычислений и моделирования либо двумерного сечения в двумерных задачах, либо трехмерного кристалла в трехмерных задачах

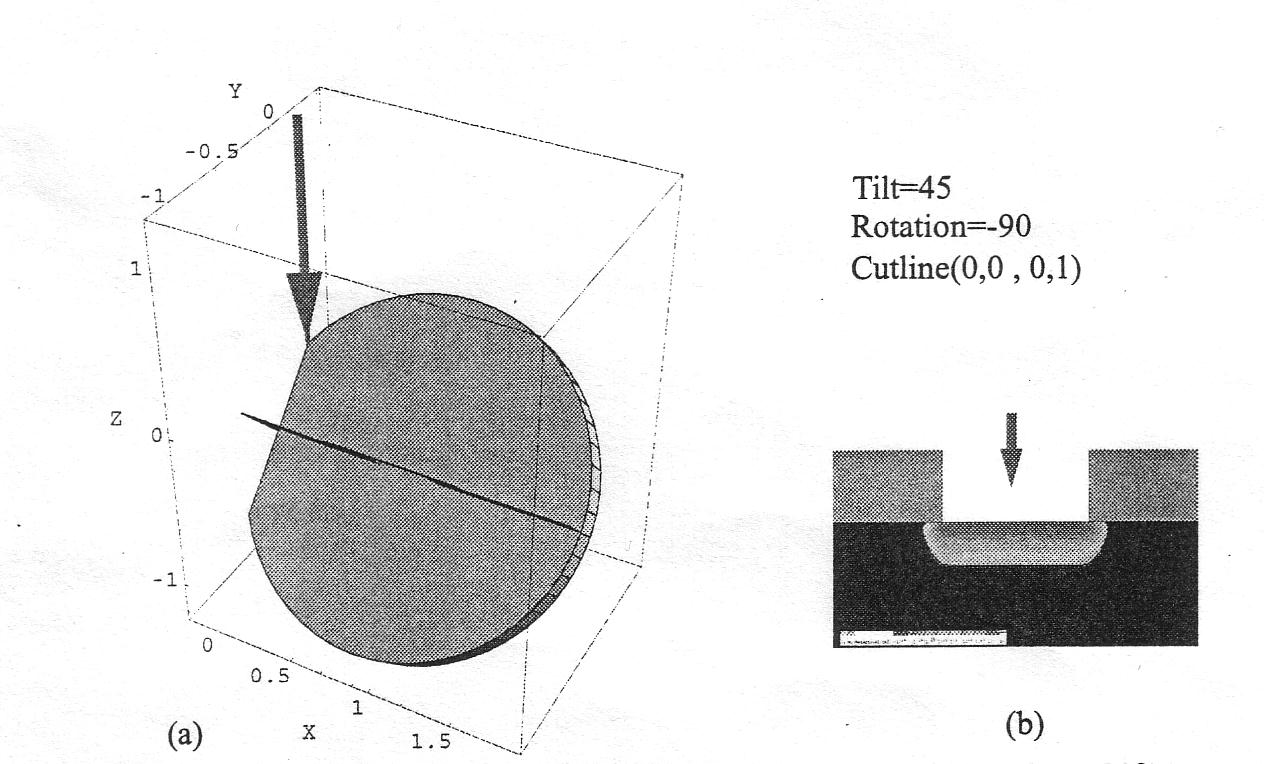
Положение пластины в установке ионной имплантации и связь первой и второй координатных систем определяется параметрами Tilt и Rotation. Третья система координат определяется через положение секущей в системе координат подложки. Положение секущей задается координатами начала (x0, y0) и конца (x1, y1) вектора секущей на поверхности подложки в операторе Cutline (x0, y0, x1, y1). Наклон подложки - вращение вокруг направления базового среза задается углом Tilt. Поворот описывается, как вращение вокруг оси Z подложки и задается углом Rotation

Угол Tilt может быть определен как угол между осями Z в первой и второй системах координат, т.е. между осями Z имплантера и подложки. Угол Rotation определяется как угол между проекцией оси Z имплантера на плоскость подложки и осью Y подложки. Положительным считается направление против часовой стрелки.

8. Принцип суперпозиции при расчете функций распределения примеси.

Во время имплантации ионы внедряются в подложку через открытые участки внешней поверхности и рассеиваются внутри подложки в трех измерениях. Проекция ионного пучка в двумерной плоскости моделирования зависит от углов поворота и наклона подложки и может приводить к несимметричным профилям распределения примеси в окрестностях краев маски.

Предположим, что ионный пучок, падающий в точку внешней границы с координатами (ξ, η) создает в подложке функцию распределения Φ(x, y, ξ, η). Тогда в любой точке (x, y) внутри подложки концентрация примеси будет вычисляться как суперпозиция функций распределения, исходящих от всех точек падения ионного пучка, т.е. от всех точек внешней границы структуры:

Для того чтобы сравнивать концентрацию имплантированных ионов с экспериментальными одномерными ВИМС – профилями, двумерный профиль представляется как произведение двух ортогональных функций: основной функции fp(x) и латеральной функции fl(y):

fp(x) fl(x)

9. Аналитические аппроксимации распределения ионов. Функции Гаусса.

В соответствии с классической теорией ЛШШ и диффузионной моделью Бирсака профили имплантированных ионов должны описываться гауссовскими распределениями. Аппроксимация распределения ионов по нормальному закону - распределение Гаусса является симметричным распределением и характеризуется двумя параметрами:

N(x)=

где D – доза имплантированной примеси, см^-2, Rp-средняя проекция пробега ионов, сигма - среднеквадратичное отклонение проекции пробега.

П ри слабой асимметрии используется двойное сопряженное распределение Гаусса (асимметричное):

N(x)=

= = , где - ф-я ошибок