31. Основные этапы численного моделирования процесса окисления. Модель Массуда для начального этапа процесса окисления.

Основные процессы, учитываемые при численном моделировании окисления: 1) химические реакции на границах раздела слоев, состоящие из растворения частиц; 2) реакции частиц с материалом слоя; 3) образование нового слоя; 4) сегрегация примеси на границах раздела слоев; 5) диффузия примеси; 6) экранирование потоков частиц слоями и границами раздела; 7) механическая деформация слоевой структуры как результат протекания химических реакций.

Расчет окислительного процесса: 1) решение уравнения растворения – диффузии – химической реакции для частиц окислителя, т.е. расчет процесса диффузии частиц окислителя с граничными условиями на границах раздела в виде уравнений химических реакций/растворения; 2) оценка скоростей образования и поглощения на границе раздела и определение граничных условий для расчета механических напряжений; 3) расчет механических напряжений; 4) вычисление граничных условий и решение уравнения диффузии примеси; 5) расчет изменения толщин слоев; 6) локальное обновление сетки в окрестности движущихся границ раздела, интерполяция концентраций, если необходимо, полное обновление сетки.

Модель Массуда: позволяет с более высокой точностью моделировать ускоренный начальный этап окисления за счет введения дополнительных параметров С и L, определяющих начальный этап роста окисла: . В присутствии N₂O (оксинитридизация) скорость роста снижается:

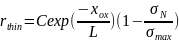
32. Моделирование окисления в присутствии маски. Аналитическая модель.

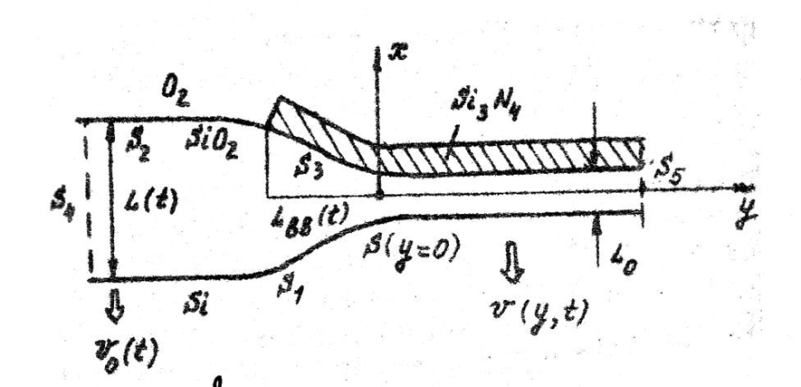
L(y,t) – одномерная толщина окисла в любой точке y, L0 – начальная толщина буферного слоя, L(t) – толщина окисла вне нитридной маски, определяемая по закону Дила – Гроува, γ – параметр бокового распространения окисла под маской.

33. Моделирование окисления в присутствии маски. Граничные условия.

S1:скорость движения границы Si – SiO₂ пропорциональна потоку окислителя F: V=(1-b)F/N

где b = 0.44 – отношение объема кремния, перешедшего в окисел, к объему окисла (коэффициент поглощения кремния окислом), N – число молекул окислителя в единице объема окисла.

S2: граница окисла как вязкой жидкости определяется поверхностным натяжением, т.е. разностью давлений внутри и вне (рАТМ) жидкости: p – p_АТМ = - γ/R,

где γ – коэффициент поверхностного натяжения, R – локальный радиус кривизны поверхности.

S 3: под маской жидкость не проскальзывает, а прилипает, что выражается условием

t - единичный вектор, касательный к поверхности

S4, S5: на линиях симметрии структуры перемещение и давление равны нулю

n - единичный вектор нормали к поверхности

?34. Моделирование окисления в присутствии маски. Численные модели с учетом вязкоупругих свойств.

К ремний, по умолчанию, считается упругим материалом. Диоксид и нитрид кремния рассматриваются как вязкоупругие материалы. Вязкая модель. При температурах окисления выше 950˚С окисел можно рассматривать как вязкую жидкость. Тогда движение его границ определяется процессом вязкого течения согласно уравнению:

где - плотность и вязкость стекла, v – скорость движения элементов, p – давление, f – грав. сила. Большая вязкость и относительно малая скорость роста (v< 1 нм/с) позволяют пренебречь в этом уравнении грав. и ускоряющим членами. Тогда имеем уравнение Навье – Стокса, где вязкая сила урав-ся градиентом давления

. В предположении, что окисел можно считать несжимаемой жидкостью, то уравнение непрерывности потока для вязкого течения несжимаемой жидкости имеет вид

. Если окисел нельзя считать несжимаемым, необходимо задать соотношение между давлением и плотностью окисла. Вязкоупругая модель. Если принимать во внимание упругопластичные свойства окисла и рассматривать его при температуре окисления как сжимаемую жидкость, то необходимо учитывать уравнение, описывающее соотношение между давлением и плотностью, а также рассчитывать механические напряжения в структуре. В этой модели принимается линейная зависимость между механическим напряжением и тензором деформаций в окисле. Причины возникновения механических напряжений: рост материала; уплотнение материала; различие коэффициентов термического расширения у различных материалов; изменение параметров кристаллической решетки кремния в присутствии германия или углерода.