2. Обоснование возможности сокращения длительности импульса излучения теа-со2 лазеров.

Как говорилось ранее, ТЕА- СО₂ лазеры работают в импульсном режиме и позволяют получать большой энергосъем с единицы объема разряда (10-50 Дж/л).

Для предотвращения дугового разряда используется также тот или иной тип ионизации, которая предшествует возбуждающему импульсу напряжения (предионизация). На рис.2 приведена схема, которая часто применяется на практике и в которой ионизация обеспечивается сильным УФ – излучением нескольких искр, которые пробегают параллельно оси трубки. Излучение этих искр в дальней УФ – области приводит к необходимой ионизации посредством как фотоионизации составляющих смеси, так и благодаря индуцированной УФ – излучением эмиссии электронов из электродов (УФ – предыонизация). К другим методам

Рис.2. Схематическое представление (вдоль лазерной оси) лазера, накачиваемого поперечным разрядом с использованием УФ-излучения от искрового источника для предыонизации газа.

предыонизации относятся использование импульсных источников пучка (предионизация электронным пучком) и ионизация благодаря коронному эффекту (коронная предыонизация). Как только произошла ионизация во всем объеме лазерного разряда, закорачивается быстродействующий вентиль (водородный тиратрон или разрядный промежуток) и через электроды разряда проскакивает главный разрядный импульс. Поскольку поперечные размеры лазерного разряда обычно велики (несколько сантиметров), то зеркала резонатора часто выбирают таким образом, что бы они образовывали неустойчивый резонатор. При низкой частоте повторения импульсов (порядка 1 Ггц) нет необходимости в прокачке газовой смеси. При более высоких частотах повторения импульсов (вплоть до нескольких килогерц) газовая смесь прокачивается в перпендикулярном оси резонатора направлении и охлаждается в соответствующем теплообменнике. Другой интересной характеристикой этих лазеров являются их относительные полосы генерации (~4 Ггц при р = 1 атм благодаря столкновительному уширению). Таким образом в ТЕА-лазерах в режиме синхронизации мод были получены оптические импульсы длительностью менее 1 нс.

К методике синхронизации продольных мод близко примыкает техника так называемой модуляции (включения) добротности, приводящая к генерации так называемых гигантских импульсов. По существу отличаясь от синхронизации мод и будучи близкой к ней только некоторыми техническими приемами, методика модуляции добротности возникла как способ управления поведением во времени импульсной генерации твердотельных лазеров. Суть дела здесь сводится к следующему. Пусть свойства активной среды лазера таковы, что в ней реализуется накачка со скоростью λ. Тогда лазер, по идее, способен излучать непрерывно мощность Рнп = hv λ. За время жизни τ_ж верхнего лазерного уровня этой мощности соответствует энергия W = hv λ τ_ж = Рнп τ_ж.

Допустим теперь, что накачка осуществляется, а условия для генерации отсутствуют, так как зеркала резонатора каким-то образом выведены из рассмотрения, например перекрыты поглощающим фильтром. Тогда энергия накачки, накапливаясь на верхнем лазерном уровне, не излучается, то есть этот уровень не опустошается радиационно. Однако ввиду конечности времени жизни уровня τ_ж на нем не может быть накоплена энергия, большая W. Пусть теперь быстро, практически мгновенно, введены зеркала резонатора, скажем, путем исключения перекрывающих зеркала поглощающих заслонок. Это означает, что произойдет быстрое включение добротности резонатора. Если к моменту включения добротности за счет накопления энергии условия самовозбуждения будущего лазера хорошо перевыполняются, вся эта энергия излучается в одном гигантском импульсе. При длительности импульса излучения τ_ж оценка пиковой мощности дает значение

(1.2.1)

За время импульса верхний уровень опустошается.

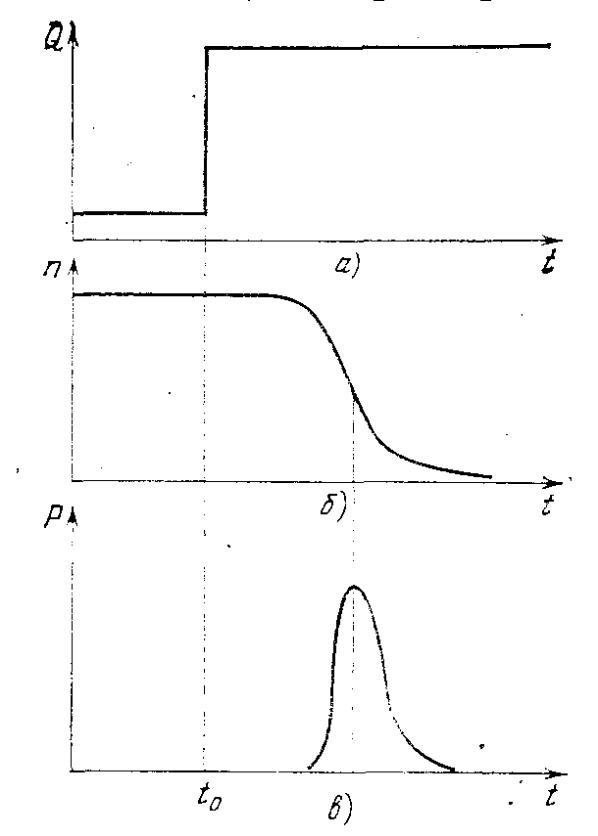
Рис.3. Включение добротности: а) изменение добротности, б) инверсии, в) мощности излучения (в произв. ед.).

Рис. 3 показывает последовательность событий, происходящих при рез- ком включении добротности резонатора в момент t0. Применение метода включаемой добротности целесообразно тогда, когда время жизни верхнего лазерного уровня τ_ж велико. Именно тогда получаются гигантские импульсы излучения.

Рассмотрим теперь лазер в режиме включаемой добротности, считая, что включение происходит мгновенно, и пренебрегая релаксацией населенностей и действием накачки за время гигантского импульса.

Пусть при включенной добротности время жизни фотона в резонаторе составляет τ_ф. Это время жизни простым соотношением Q =ωτ_ф связано с добротностью резонатора. Так как 1/ τ_ф дает значение скорости ухода фотонов из резонатора, то скоростное уравнение для числа фотонов Ф может быть записано в виде

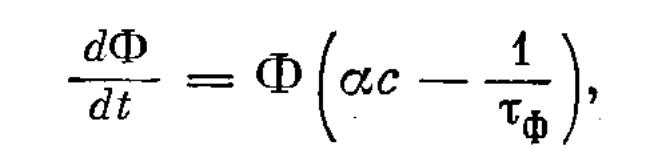(1.2.2.)

где с — скорость света, а α — коэффициент усиления активной среды. Вводя обозначение α_пор= 1/с τ_ф для порогового значения, коэффициента усиления и вспоминая, что усиление пропорционально инверсии n, мы можем переписать уравнение 1.2.2 в виде

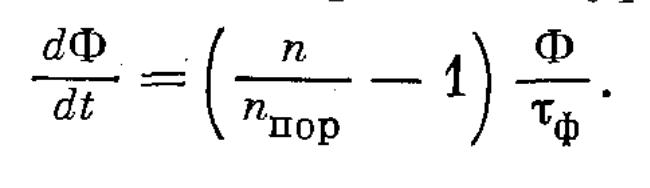(1.2.3)

Здесь n/n_пор = α/α_пор, Фn/n_пор τ_ф дает скорость нарастания числа фотонов в резонаторе, Ф/ τ_ф — скорость убывания числа фотонов в резонаторе. Нарастание превалирует над убыванием при n > n_пор. Так как каждый акт испускания одного фотона уменьшает инверсию на две единицы, то скорость убывания инверсии пропорциональна скорости нарастания числа фотонов, а коэффициент пропорциональности равен 2:

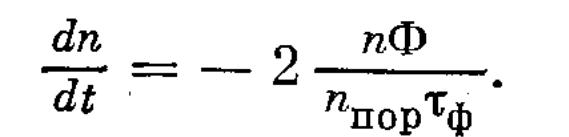(1.2.4)

Совместное решение нелинейных уравнений 1.2.3 и 1.2.4 легко осуществимо численно. Однако некоторые качественные выводы можно сделать на основе доступных аналитических решений. Разделив 1.2.3 на 1.2.4, мы получаем уравнение

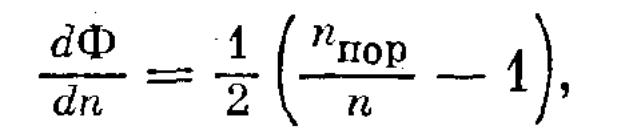(1.2.5)

решение которого известно:

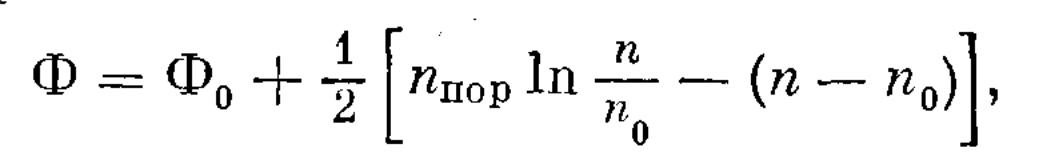(1.2.6)

где Фо и n_о —число фотонов и инверсия соответственно в начальный момент времени, т. е. в момент мгновенного включения добротности. Если считать, что Фо < Ф, тогда

(1.2.7)

Далее. Мы не знаем решения 1.2.3, то есть не знаем Ф(t). Однако очевидно, что при t > τ_ф число фотонов Ф 0. Инверсия при этом в нуль не обращается, а достигает некоторого установившегося конечного, значения n_k, которое может быть найдено при Ф = 0 из 1.2.7 решением трансцендентного уравнения

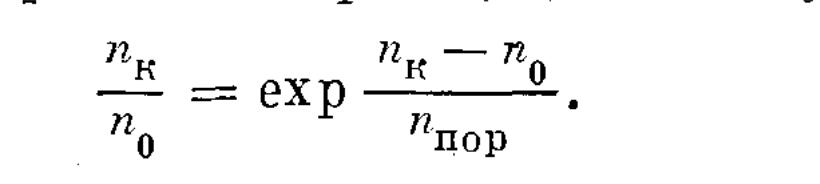(1.2.8)

Уравнение 1.2.8 можно использовать, в частности, для определения полезно используемой доли запасенной в инверсии энергии:

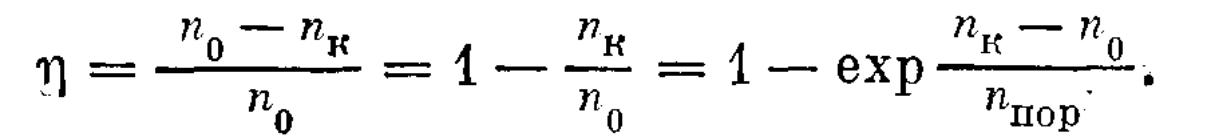(1.2.9)

Из 1.2.9 виден тот интуитивно ясный вывод, что при большом превышении начальной инверсии над пороговой (n/n_пор→ ∞) вся запасенная в инверсии энергия используется для генерации излучения: η→1.

Мощность излучения лазера очевидным соотношением:

(1.2.10)

связана с числом фотонов в резонаторе лазера Ф и временем жизни фотона τ_ф. Из 1.2.10 и 1.2.7 получаем

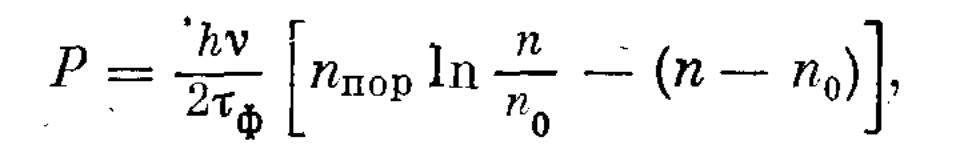(1.2.11)

где инверсия n зависит от времени: n = n(t). Если бы мы знали функцию n(t), то 1.2.11 дало бы нам форму импульса излучения. Численные решения уравнений 1.2.3 и 1.2.4 показывают, что при больших превышениях начальной инверсии над пороговой ( n>>n_пор) время нарастания (передний фронт) импульса оказывается меньшим времени жизни фотона в резонаторе τ_ф, а время спадания (хвостовая часть) импульса оказывается величиной порядка τ_ф.

Пиковую мощность гигантского импульса (импульса включаемой или модулированной добротности) можно определить с помощью 1.2.11. Из условия dP/dn = 0 следует, что максимальное значение мощности излучения в течение генерации гигантского импульса 1.2.11 достигается, когда n=n_пор При этом

(1.2.12)

что при большом превышении начальной инверсии над пороговой дает

(1.2.13)

Так как начальная инверсия n₀ имеет смысл произведения скорости накачки верхнего лазерного уровня на время его жизни (n₀=λτ_ж), то видно, что оценка 1.2.2 по существу совпадает с несколько более строго полученной формулой 1.2.13, правда, в предположении, что длительность гигантского импульса примерно равна времени жизни фотона в резонаторе.

Для осуществления режима включаемой добротности используются оптико-механические и электрооптические затворы, а также затворы на основе просветляющихся фильтров. В последнем случае сечение резонансного поглощения вещества фильтра должно быть много больше сечения резонансного усиления активного вещества: σ_фил>>σ_ус. В противном случае практически вся накопленная веществом энергия будет расходоваться на стационарное просветление фильтра. Кроме того, для обеспечения быстроты включения добротности время релаксации фильтра должно быть много короче времени жизни инверсии: τ_фил < < τ_ус.

Рассмотрим еще один режим работы лазера, который позволит сократить длительность импульсов излучения. Режим включения инверсии принято называть включением усиления. Его анализ требует решения нелинейных уравнений типа 1.2.3 и 1.2.4. При этом все выводы, сформулированные выше применительно к режиму модулированной добротности, справедливы и в рассматриваемом случае.

За время импульса при глубокой инверсии излучается энергия порядка

(1.2.14)

Пиковая мощность определяется характерным временем жизни фотона в резонаторе τ_фил = Q/ω:

(1.2.15)

Нарастание интенсивности излучения в импульсе генерации происходит со скоростью, большей 1/τ_ф, спадание — со скоростью порядка 1/τ_ф. Величина τ_ф может быть оценена выражением:

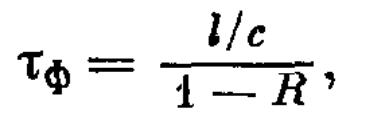(1.2.16)

что при больших коэффициентах усиления и, следовательно, малых R (R – коэффициент отражения) дает для l = 10 — 100 см (l – расстояние между зеркалами) значение τ_ф = 0,3 — 3 нс как оценку снизу.

Вернемся теперь к вопросу о к. п. д. газоразрядных лазеров.

Для импульсного режима формула

(1.2.17),

где где η_н— эффективность действия накачки, точнее, в случае газоразрядных лазеров та доля энергии накачки, вводимой в разряд, которая тратится на возбуждение верхнего лазерного уровня, энергия этого уровня обозначена символом Ев, несправедлива. Как мы знаем, после включения инверсии индуцированное излучение идет до тех пор, пока не выровняются населенности. Часть населенности верхнего уровня не используется. В отсутствие вырождения эта часть составляет 1/2 — значение, использованное при приведенных выше оценках. При наличии вырождения эта часть зависит от соотношения статистических весов верхнего и нижнего уровней g_B и g_н и составляет g_н/(g_н + g_в). В результате к. п. д. лазера на самоограниченных переходах записывается в виде

(1.2.17)

где

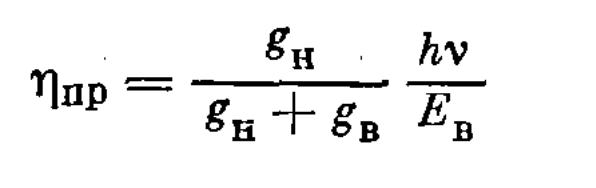(1.2.18)

есть предельный к. п. д. перехода, достигаемый тогда, когда вся энергия тратится на возбуждение верхнего уровня энергии Ев. По существу, η_пр является лазерной характеристикой перехода. Множитель g_н/(g_н + g_в) обычно заключен в пределах 1/3—2/3. Отношение hv/EB для атомов с невысоким нижним уровнем может составлять 0,5—0,7. Следовательно, можно надеяться найти такие переходы, для которых η_пр = 0,3—0,5. Сложнее оценить величину η_н. Эксперимент свидетельствует о возможности получе- ния с учетом энергозатрат на создание плазмы значения η_пр = 0,3—0,5. В результате полный к. п. д. может составлять 10— 20%, что явилось бы очень высоким достижением.

В данном параграфе мы рассмотрели два метода сокращения длительности импульса – метод модуляции добротности и режим переключения усиления. Так же излучения малой длительности можно генерировать увеличивая давление активной среды и энерговклад, а так уменьшая длину резонатора и снижая его добротность.

Рис.4. Зависимость длительности излучения импульса в смеси СО₂:N₂ = 1:1

Выводы:

Сократить длину излучения импульса можно: