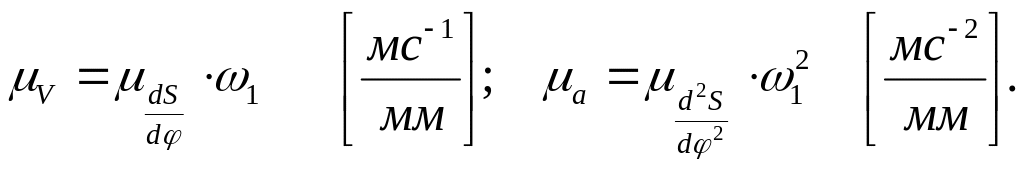2. Графический метод динамического синтеза кулачкового механизма с поступательно движущимся роликовым и остроконечным толкателем

( Приложение 1,2 ).

2.1. Построение кинематических диаграмм

Проектирование кулачкового механизма начинают с построения кинематических диаграмм аналогов ускорения и скорости, а также перемещения. Исходными данными для построения диаграмм могут быть заданный закон изменения аналога ускорения, максимальное и минимальное значения аналога ускорения (или их отношение), рабочий угол профиля кулачка, фазовые углы, угловая скорость кулачка.

По данным для проектирования строится диаграмма изменения аналогов ускорений (рис.8). По оси ординат желательно отложить отрезок, изображающий максимальное значение аналога ускорения, равный 70–80 мм. По оси абсцисс откладывается рабочий угол профиля ведущего звена кулачка. Рекомендуется принять отрезок ℓ_φ, изображающий рабочий угол профиля кулачка, равным 180–300 мм.

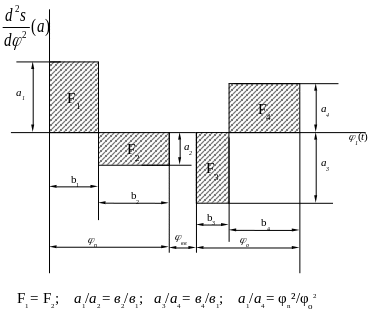
В том случае, когда задано отношение максимального аналога ускорения к минимальному y=а₁/а₂, а углы подъема (удаления) и опускания (приближения) не равны, но законы для них одинаковы, то при построении диаграммы необходимо выдержать равенство площадей F₁=F₂, F₃=F₄, (рис.7) т.е. а₁/а₂=в₂/в₁; а₃/а₄=в₄/в₃. Кроме того должно выполняться равенство

а₁/а₄ = φ_n²/φ_y².

Построение кинематических диаграмм на конкретном примере рассмотрено в приложении1.

Построив заданную диаграмму аналога ускорений толкателя в зависимости от угла поворота кулачка (d²s/dφ₁²=f(φ₁)) и графически проинтегрировав ее, получим диаграмму аналога скорости толкателя в зависимости от угла поворота кулачка ds₂/dφ₁=f(φ₁).

l_φ

Рис.8

Метод графического интегрирования заключается в следующем. Углы подъема и опускания диаграммы d²s₂/dφ₁=f(φ₁) разбиваем по оси φ на 810 участков (0–1; 1–2; 2–3; и т.д.) и плавную кривую заменяем ступенчатой из условия равенства площадей, ограниченных обеими диаграммами. Для этого необходимо, чтобы на каждом участке площади заштрихованных площадок, расположенных по обе стороны кривой, были равны. Это достаточно точно устанавливается на глаз.

Выбираем на оси абсцисс слева от начала координат на произвольном расстоянии H_а точку р. Соединим эту точку с точками 1, 2, 3 и т.д. ступенчатой диаграммы лежащими на оси ординат, получим лучи р–1; р–2; р–3; и т.д.

Под диаграммой d²s₂/dφ₁²=f(φ₁) проводим оси координат диаграммы ds₂/dφ₁=f(φ₁) и разбиваем ось φ на участки, равные соответствующим участкам диаграммы d²s₂/dφ₁²=f(φ₁). Далее на участке 0–1 проводим из начала координат отрезок 0–1, параллельный лучу р–1; из полученной точки 1 на участке 1–2 проводим отрезок 1–2 параллельный р–2; из точки 2 проводим отрезок 2–3, параллельный лучу р–3 и т.д. Полученная ломаная линия представляет собой диаграмму ds₂/dφ₁=f(φ₁) (аналога скорости толкателя в функции угла поворота кулачка). Заменяем ломаную линию плавной кривой и еще раз графически интегрируем, выбрав по возможности полюсное расстояние Полученная кривая – зависимость перемещения толкателя от угла поворота кулачка (s₂=f(φ₁)).

Масштабные коэффициенты диаграмм определяются следующим образом:

где h – заданный ход толкателя, в м;

smax – максимальная ордината диаграммы s₂=f(φ₁), в мм;

где

φ_{р =} φ_{у +} φ_{вв +} φ_п – рабочий угол профиля в рад. ;

ℓ_φ – отрезок, изображающий рабочий угол на диаграмме, в мм;

H_V – полюсное расстояние.

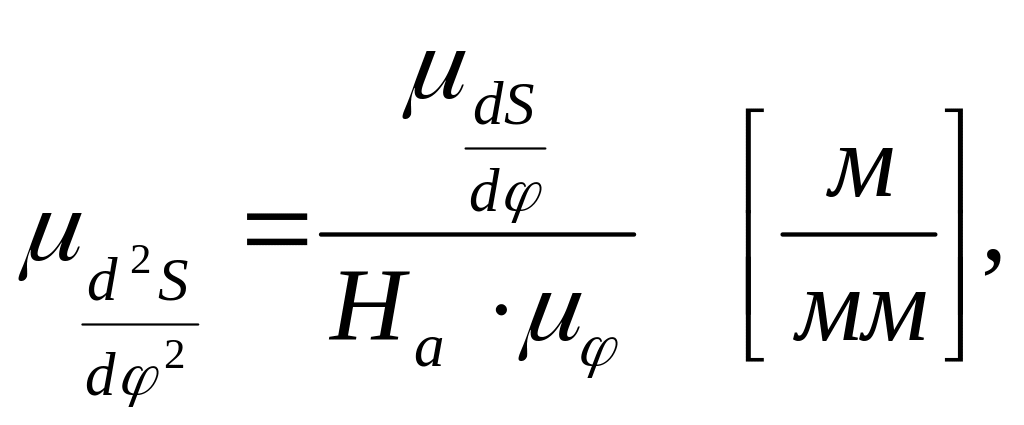
где H_а – полюсное расстояние, в мм .

В том случае, когда ω_кул.=const полученные диаграммы одновременно являются диаграммами ускорения (а₂=f(t)), скорости (V₂=f(t)) и перемещения (s₂=f(t)) толкателя.

Масштабные коэффициенты этих диаграмм определяются:

где ω₁=ω_кул. – угловая скорость кулачка;