2.3 Методические указания

В некоторых случаях возникает необходимость преобразования структурных схем для получения эквивалентной (расчетной) передаточной функции исследуемой системы. Такая ситуация возникает в том случае, если исходная структурная схема является многоконтурной. Причем многоконтурная система без перекрестных связей преобразуется к одноконтурной довольно просто - достаточно использовать правила преобразования последовательного соединения звеньев САУ, параллельного соединения звеньев САУ и присутствия обратной связи.

Для преобразования многоконтурной САУ с перекрещивающимися связями к одноконтурной, кроме упомянутых выше правил, необходимо использовать правила переноса звена через узел, звено, элемент сравнения через звено и обратно.

Пусть замкнутая система управления задана структурной схемой (рис.3):

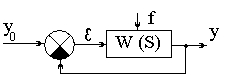
Рис. 3.

Замкнутая САУ может быть .описана несколькими передаточными функциями: Ф(S)=Y(S) - передаточная функция по управляющему воздействию (главная передаточная функция);

Ф_ε(S)⁼ Е(S)/Y₀(S) -передаточная функция по ошибке;

Ф_f(S)=Y(S)/F(S) - передаточная функция по возмущению;

Ф_{ε f}(S)= Е(S)/ F(S) - передаточная - функция для ошибки возмуще­ния.

Оригиналы и изображения связаны следующим образом:

y₀(t)÷Y₀(S); ε(t) ÷Е(S); f(t) ÷ F(S); y(t) ÷Y(S).

Имея в виду, что W(S) = В(S)/А(S), можно указать на следую­щий связи передаточных функций замкнутой САУ с передаточной функцией ее разомкнутой части:

Ф(S)= = , (2.1)

Ф_ε (S) = 1- Ф(S) = = , (2.2)

Ф_f(S) = = , (2.3)

где W_f(S) - передаточная функция части разомкнутой системы, к которой приложено возмущение f(t); R(S)= A(S) · W_f(S) полином степени не выше, чем ступень полинома A(S).

Ф_{ε f}(S)= Ф_f(S), (2.4)

Нетрудно заметить, что знаменатели всех передаточных функций идентичны. Это дает возможность высказать важный вывод: характеристическое уравнение замкнутой САУ может быть записано по любой из имеющихся передаточных функций системы.

Для получения требуемых частотных функций следует исполь­зовать передаточную функцию W(S). При этом после замены S=jw получается комплексная передаточная функция W(jw), который следует представить в виде вещественной и мнимой слагаемых:

W(jw)=P(w)+jQ(w). (2.5)

Теперь КЧХ можно построить в координатах P и Q. Амплитудная частотная и фазочастотная функции получаются из условий:

A(w)= , φ(w)=arctg . (2.6)

Для получения выражений и построения частотных характеристик можно использовать и другой подход, учитывающий свойства последовательного соединения звеньев.

Передаточные функции (I)-(4) получены в предположении, что главная обратная связь единичная. Если это не так, то соотношения (I)-(4) необходимо соответствующим образом скорректировать. Пусть разомкнутая часть САУ имеет передаточную функцию W(S)=B(S)/A(S). Тогда характеристический полином замкнутой САУ, на основании записей (I)-(4) имеет вид:

Д(S)=A(S)+B(S). (2.7)

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ:

1. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. - Изд. 4 -е, перераб. и доп. – СПб., Профессия, 2007. – 752 с. – (Серия: Специалист).

2. Бесекерский В.А., Герасимов А.Н., Лучко С.ВА., Небывалов А.В., Порфирьев Л.Ф., Фабрикант Е.А., Федоров С.М., Цветков В.И. Сборник задач по теории автоматического регулирования и управления: изд. пятое, перераб. – Наука, гл. ред. физ-мат. лит., 1978. – 512 с.

3. Теория автоматического управления: ч. I: Теория линейных систем автоматического управления: Учебное пособие для вузов/ Под. Ред. Воронова А.А. – М.: Высшая школа, 1977. – 303 с.: ил.

4. Теория автоматического управления: ч.II: Теория нелинейных систем автоматического управления: Учебное пособие для вузов/ Под ред. Воронина А.А. – М.: Высшая школа, 1977. – 288 с.: ил.

24