1. По допускаемым напряжениям

На статическую прочность: Для валов _экв.max.= K _экв≤[] ₊₁

Для оси _max = К _и ≤[] ₊₁

К – коэффициент перегрузки

На сопротивление усталости: Для валов σ_экв=≤[] _-1

Для оси _и ≤ [] _R

[] _R =[] _-1 - для вращающейся оси;

[] _R =[] ₀ - для невращающейся оси.

В методе расчета по допускаемым напряжениям напряжения при изгибе находят одновременно от вращающихся и невращающихся нагрузок. Направление вращающихся берется самое неблагоприятное, когда их действие суммируется с действием невращающихся нагрузок.

Недостатками метода расчета по допускаемым напряжениям являются неучёт разного характера действия нагрузок, а также разная чувствительность

материала к асимметрии цикла при нормальных и касательных напряжениях.

2. По запасам прочности.

При расчете по запасам прочности необходимо прежде всего установить характер цикла напряжений. Вследствие вращения вала напряжения изгиба в различных точках его поперечного сечения изменяются по симметричному циклу, даже при постоянной нагрузке (исключение составляют случаи, когда нагрузка вращается вместе с валом).

Напряжения кручения изменяются пропорционально изменению нагрузки. В большинстве случаев трудно установить действительный цикл нагрузки машины в условиях эксплуатации. Тогда расчет выполняют условно по номинальной нагрузке, а циклы напряжений принимают - симметричным для напряжений и згиба (см. рис. а) и отнулевым для напряжений кручения (см. рис. б). Выбор отнулевого цикла для напряжений кручения обосновывают тем, что большинство машин работает с переменным крутящим моментом, а знак момента изменяется только у реверсивных машин. Неточность такого приближенного расчета компенсируют при выборе запасов прочности.

В этом методе изгибающие моменты и напряжения изгиба находят отдельно:

1.для вращающихся нагрузок М_ив=М_в, _ив=М_ив/W

2.для невращающихся нагрузок М_ин=(М_Y²+ М_Z²)^0,5 , _ин=М_ин/W

Далее устанавливаются:

1.амплитудные напряжения _а=_ин

2. средние нормальные напряжения _m=_ив.

Касательные напряжения устанавливаются в зависимости от цикличности напряжений:

-при нереверсивном моменте Т _а=_m=_к/2 - отнулевой цикл напряжений;

-при реверсивном моменте _а=_к ; _m=0 - симметричный цикл напряжений.

Тогда проверка:

На статическую прочность:

Запасы прочности:

по нормальным напряжениям: , где _и = _а+_m.

по касательным напряжениям:

Общий запас прочности:

На сопротивление усталости:

Запасы прочности: ; ;

Общий запас прочности: .

- эквивалентная амплитуда нормальных напряжений

- эквивалентная амплитуда касательных напряжений

- коэффициент долговечности (числа циклов).

- эквивалентное число циклов

- показатель кривой усталости

- коэффициенты чувствительности к ассиметрии цикла при изгибе и кручении

- коэффициенты концентрации напряжений в опасном сечении при изгибе и кручении

Здесь: k_σ; k_τ - эффективные коэффициенты концентрации напряжений

(для ступенчатых галтельных переходов; для шпоночных пазов; для шлицевых и резьбовых участков валов и т. п.) определяют:

1. по ГОСТ 25.504 – 82

2 . по таблицам справочников.

k_d - коэффициент, учитывающий размеры вала (масштабный фактор);

k_F - коэффициенты, учитывающий качество (шероховатость) поверхности;

k _V - коэффициент, учитывающий наличие поверхностного упрочнения

При действии в расчетном сечении нескольких источников концентрации напряжений учитывают наиболее опасный из них (с наибольшим значением k_σd или k_τd ).

На практике нередки случаи, когда диаметр вала определяется не прочностью самого вала, а прочностью подшипников. Поэтому расчеты вала и подшипников взаимосвязаны.

Проверка валов на жесткость.

У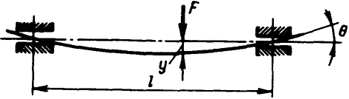 пругие перемещения вала отрицательно влияют на работу связанных с ним деталей: подшипников, зубчатых колес, катков, фрикционных передач и т. п. От прогиба вала (рис.) в зубчатом зацеплении возникает концентрация нагрузки по длине зуба. При больших углах перекоса θ в подшипнике может произойти защемление вала (см. правую опору на рис.). В металлорежущих станках перемещения валов (в особенности шпинделей) снижают точность обработки и качество поверхности деталей. В делительных и отсчетных механизмах упругие перемещения снижают точность измерений и т. д. Необходимо , чтобы упругие деформации – прогибы и перекосы не превосходили допускаемых величин. Расчеты на жесткость, как правило, носят проверочный характер и ведутся по долговременно действующим нагрузкам. Перемещения при изгибе в общем случае целесообразно определять, используя интеграл Мора и способ Верещагина (см. курс "Сопротивление материалов"). Для простых расчетных случаев можно использовать готовые решения, приведенные в табл. При этом вал рассматривают как имеющий постоянное сечение некоторого приведенного диаметра.

Допускаемые упругие перемещения зависят от конкретных требований к конструкции и определяются в каждом отдельном случае.

Для вала зубчатых передач стрела прогиба под колесом

[у] ≈ 0,01m - передачи цилиндрические;

[у] ≈ 0,05m - конические, гипоидные, глобоидные передачи,

где m - модуль зацепления.

Угол взаимного наклона валов под шестернями γ < 0,001 рад.

В станкостроении для валов общего назначения [у] = (0,0002...0,0003)ℓ,

где ℓ - расстояние между опорами.

Угол перекоса вала в подшипнике скольжения [θ] = 0,001 рад;

в радиальном шарикоподшипнике [θ] = 0,005 рад.

Максимальный угол закручивания определяется также по формулам курса "Сопротивление материалов": φ=Тℓ∕GJ≤[φ]

Допускаемый угол закрутки в градусах на метр длины можно принимать равным: [φ]=0,25 ^o...0,35 ^o

Малое значение допускаемых перемещений иногда приводит к тому, что размеры вала определяет не прочность, а жесткость. В этих случаях нецелесообразно изготовлять вал из дорогих высокопрочных сталей (если это не диктуется какими-либо другими условиями, например износостойкостью цапф).

РАСЧЁТ ВАЛОВ НА КОЛЕБАНИЯ

В ынужденные колебания системы с одной степенью свободы (простейший случай колебания вала на рис. Здесь на валу, вращающемся с угловой скоростью ω_в, закреплен диск массой m с эксцентриситетом е.) описывают уравнением

У= F_a sin ω_вt∕m( ω_c²- ω_в² )

у - амплитуда вынужденных колебаний массы m ;

F_a- амплитуда возмущающей силы F(t) =F_a sin ω_вt ;

ω_в - круговая частота возмущающей силы или частоты вынужденных колебаний системы;

ω_с - круговая частота свободных колебаний системы.

Собственную массу вала считаем малой по сравнению с m и в расчет не принимаем (упругая система с одной степенью свободы).

На вал действует центробежная сила F_a =m ω_в²e, вектор которой вращается с угловой скоростью ω_в.

Частота собственных изгибных колебаний ω_с=(g|y_ст) ^0,5

у_ст - статический прогиб вала от действия силы тяжести mg диска.

Частоту вращения , при которой наступает резонанс, называют критической:

n_кр= 30ω_с/π=30(g|y_ст) ^0,5/ π

За предел вибрационной устойчивости обычно принимают:

для жестких валов n≤0,7n_кр,

для гибких валов n≥1,3n_кр.