График выборочной (черный) и теоретической (серый) функций распределения

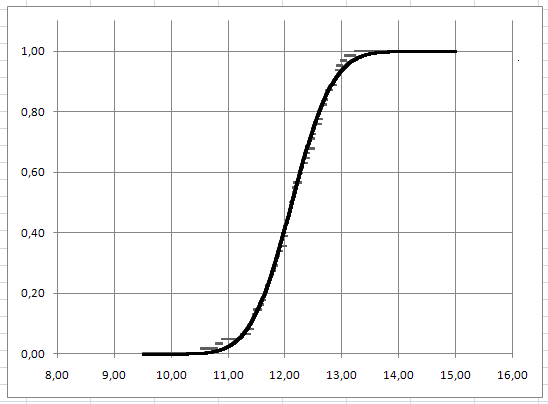
Рис. 1

f(R6) – плотность распределения. Функция задается с помощью функции НОРМРАСПР, (в строке Интегральная – 0).

График теоретической плотности распределения

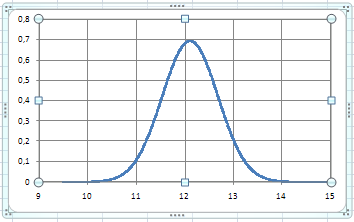Рис.2

Для построения гистограммы воспользуемся пакетом анализа→ гистограмма.

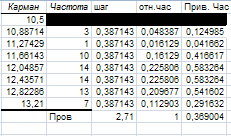
Карман - середины интервалов группировки.

Интегральный процент – накопленные частоты в процентах.

Частота - количество выборочных значений, которые попали данный интервал (карман).

Шаг – постоянная величина, равная разности двух соседних карманов.

Относительная частота – отношение частоты к числу элементов выборки.

Сумма всех относительных частот должна быть равна 1 !

Приведенная частота –отношение относительной частоты к шагу.

На основе полученного анализа строит гистограмму приведенных частот.

Гистограмма относительных частот

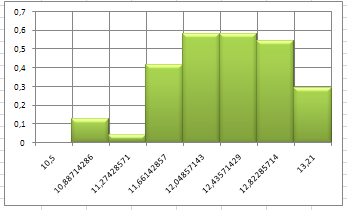
Рис.3

Так как теоретическая функция распределения F(R6) с нормальным распределением с параметрами:

M(R6)= 12,1049

D(R6)= 0,3249

𝜎(R6)= 0,5700

мало отличается от выборочной функции распределения F^*(R6)(это следует из рис. 1), то гипотеза о том, что случайная величина R6распределена нормально с параметрами:

M(R6)= 12,1066

D(R6)= 0,3301

𝜎(R6)= 0,5745

не противоречит выборочным данным. Это же подтверждается сравнением графика плотности распределения (рис.2) и гистограммы приведенных частот (рис.3)

Создаём: лист Корреляционный анализ.

Определим коэффициенты корреляции.

В статистическом анализе вычисляется коэффициент корреляции (коэффициент Пирсона), его можно вычислить по формуле:

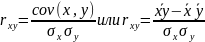
Линейный коэффициент корреляции характеризует степень тесноты не всякой, а только линейной зависимости.

В общем случае, когда величины когда величины xиy связаны произвольной вероятностной зависимостью, линейный коэффициент корреляции принимает значение в пределах 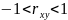, тогда качественная оценка тесноты связи xи y может быть выявлена на основе шкалы Чеддока.

Создаем новый лист Корреляционный анализ и копируем все сопротивления и найденные токи без нулевой строки, отделив величины для различения закрашенным столбцом.

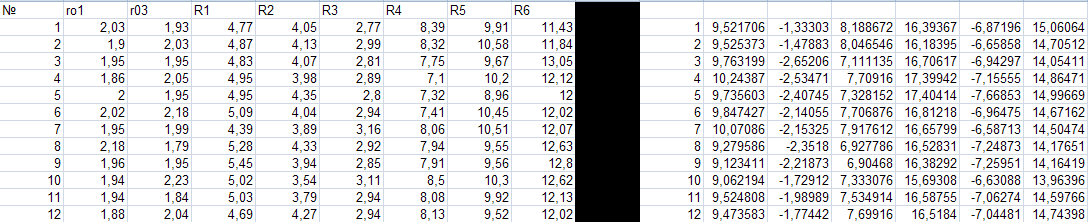
Составляем корреляционную матрицу.

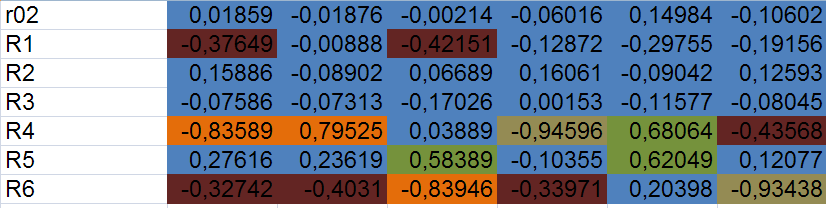
Находим коэффициент корреляции r_RIс помощью функции: КОРРЕЛ, выбирая соответствующие массивы сопротивлений и токов. Воспользовавшись таблицей Чеддока, определим качественную оценку тесноты связи величин сопротивлений R и токовI.

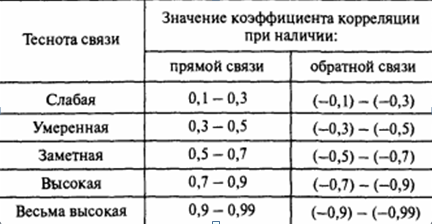
Таблица Чеддока

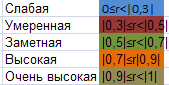
Воспользовавшись панелью Условное форматирование, создадим 6 правил, с помощью которых закрасим нашу таблицу по цветам, соответствующим определенному коэффициенту корреляцииr_RI.

Создаём: листРегрессионный анализ.

Регрессионный анализ заключается в определения аналитического выражения связи зависимости случайной величины Y с независимыми случайными величинами X₁, X₂, X₃…X_n. Форма связи результативного признака Y с факторами X₁, X₂, X₃…X_n получила название уравнение регрессии.

Форма связи результативного признака Y с факторами выбранного уравнения различают линейную и нелинейную регрессию. В зависимости от числа выбранных признаков различают парную и множественную регрессию.

Пусть у нас есть случайные величины сопротивления и ток. Предположим, что между этими величинами существует статистическая линейная зависимость. Составим уравнение множественной регрессии:

Проверим эту зависимость. Создаем новый лист Регрессионный анализ, куда вводим все сопротивления r01, r02, R1, R2, R3, R4, R5, R6 и ток, у которого большой по модулю коэффициент корреляции. В нашем случае I4, у него самый большой коэффициент r_RI=-0,945. Проводим регрессионный анализ с помощью пакета анализа → Регрессия.

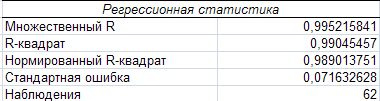
Проверим полученную модель на адекватность. Модель адекватна если R²>0,7. В нашем случае,R²=0,99045457>0,7. Следовательно, модель адекватна.

Получаем три незначимых коэффициента: r01, R2,R3 так как нижние и верхние пределы имеют различные по знакам значения, и ноль входит в этот интервал.

С учетом незначимых коэффициентов, проводит второй регрессионный анализ.

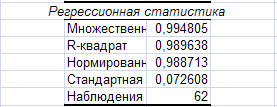
1. МножественныйR – коэффициенту корреляции;

2. R-квадрат – коэффициенту детерминации R²;

3. Стандартная ошибка – остаточному стандартному отклонению

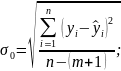
4. Наблюдения – числу наблюдений n;

Столбцы в таблице «Дисперсионный анализ» имеют следующую интерпретацию:

1. Столбец df - число степеней свободы.

Для строки Регрессия число степеней свободы определяется количеством факторных признаков т в уравнении регрессии .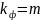

Для строки Остаток число степеней свободы определяется числом наблюдений пи количеством переменных в уравнении регрессии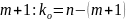

Для строкиИтого число степеней свободы определяется суммой:

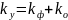
2. 2. Столбец SS - сумма квадратов отклонений.

Для строки Регрессия — это сумма квадратов отклонений теоретических данных от среднего:

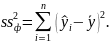
Для строки Остаток - это сумма квадратов отклонений эмпирическихданных от теоретических:

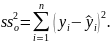
Для строкиИтого - это сумма квадратов отклонений эмпирическихданных от среднего:

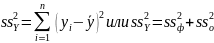
3. Столбец МS- дисперсии, рассчитываемые по формуле

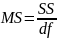
Для строки Регрессия — это факторная дисперсия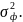

Для строки Остаток - это остаточная дисперсия

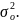
Столбец F - расчетное значение F-критерия Фишера Fp, вычисляемое по формуле:

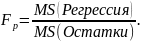
4. Столбец Значимость F- значение уровня значимости, соответствующее вычисленному значению F_p.Определяется с помощью функции

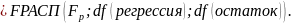
Столбцы этой таблицы имеют следующую интерпретацию:

5. Коэффициенты - значения коэффициентов

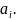
6. Стандартная ошибка - стандартные ошибки коэффициентов

7. t-статистика - расчетные значения t-критерия, вычисляемыепо формуле:

8. Р-Значение - значения уровней значимости, соответствующие вычисленным значениям /р. Определяются с помощью функции:

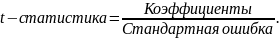
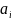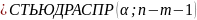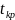9. Нижние 95 % и Верхние 95 % — соответственно нижние и верхние границы доверительных интервалов для коэффициентов регрессии . Для нахождения границ доверительных интервалов с помощью функции рассчитываются критическое значение t-критерия , а затем по формулам:

Нижние 95% = Коэффициент – Стандартная ошибка* ;

Верхние 95% = Коэффициент + Стандартная ошибка*

Вычисляются соответственно нижние и верхние границы доверительных интервалов.

Графики остатков показывают компактное распределение величини говорят об адекватности модели, так как точки пучкуются в одном месте, а не растягиваются и не вылезают.

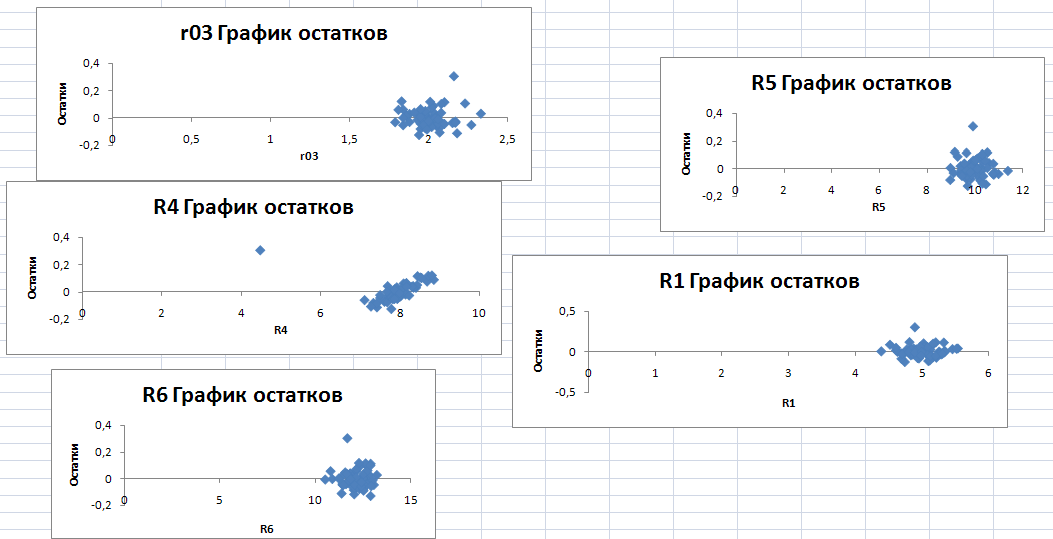
Проверим гипотезы о значимости коэффициента детерминации R² для последнего регрессионного анализа.

В математической статистике доказывается, что если гипотеза Н₀ – о незначимости коэффициента выполняется R²=0, то величина Fимеет F-распределение с k=m, l=n-m-1–числом степеней свободы, то есть:

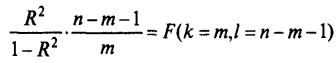
Где n – число наблюдений, m–число факторов в уравнении регрессии.

Определим с помощью функции :РАСПРОБР F_кр и сравним его с расчетным значением критерия Фишера F, найденным в дисперсионном анализе.

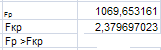
Гипотеза Н₀ – о незначимости коэффициента R²=0 отвергается, когда F>F_кр.

В нашем случае: F=1069,653161>F_кр=2,379697023. Следовательно, гипотезу о незначимости коэффициента R²=0 можно отвергнуть. Следовательно, коэффициент детерминации R², значит модель адекватна.

Выводы

В данной проделанной работе мы овладели навыками построения элек­трических схем в графическом редакторе. Познакомились с принципом работы блока Given Find. С помощью данного блока модно легко найти все токи элек­трической цепи гораздо проще, чем классическим методом расчета электриче­ских цепей.

Инструмент «Описательная статистика» позволил создать статистический отсчет, содержащий информацию о центральной тенденции изменчивости входных данных.

Критерий согласия х² гипотез о нормальности случайной величины R4 позволил установить, что гипотеза не противоречит опытным данным, и она может быть принята как достоверная. Основное преимущество этого критерия это его гибкость. Этот критерий можно применять для проверки допущения о любом распределении, даже не зная параметров распределения.

В программе Microsoft Excel получили модель электрической цепи с по­мощью, которой можно легко рассчитать значения токов при изменяющихся сопротивлениях.

Корреляционный анализ позволил установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных свя­занных с большими значениями другого набора (положительная корреляция), или, наоборот малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связанны (нулевая корреляция).

Линейный регрессионный анализ заключается в подборе графика для на­бора наблюдений с помощью метода наименьших квадратов. Регрессия исполь­зуется для анализа воздействия на отдельную зависимую переменную значений одной или более независимых переменных.