14) Поліном лагранжа Інтерполяційний многочлен Лагранжа

Побудуємо інтерполяційний многочлен Лагранжа L_n(x), який задовольняє умову (4.1).

Многочлен L_n(x) шукатимемо у вигляді лінійної комбінації спеціально сконструйованих многочленів степеня п:

.

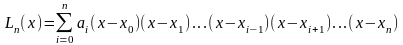Для визначення коефіцієнтів а_і (і=0,1,...,n), скористаємось вузловими умовами (4.2). Тоді шукані коефіцієнти визначаються як:

Підставивши знайдені коефіцієнти а_i, дістанемо вираз інтерполяційного многочлена L_n(x):

(4.4)

Інтерполяційний многочлен, записаний у вигляді (4.4), називається інтерполяційним многочленом Лагранжа.

Формулі Лагранжа (4.4) можна надати іншого вигляду:

,

де ,

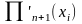- значення похідної від функції у точці х=х_і.

15) Інтерполювання сплайнами Інтерполювання функцій за допомогою сплайнів

При інтерполюванні функцій з великою кількістю вузлів інтерполяційний поліном Лагранжа має високий степінь, що спричиняє коливання полінома на проміжках між вузлами інтерполювання. Щоб зменшити степінь інтерполяційного полінома вузли інтерполювання можна розбити на групи і будувати інтерполяційні поліноми з меншою кількістю вузлів. Але в цьому разі на стиках між вузлами порушуються аналітичні властивості інтерполяційного полінома, з'являються точки розриву похідних. Позбутися цих недоліків при інтерполюванні можна за допомогою так званих сплайнів. Наочне уявлення про сплайни дають криві, побудовані за допомогою лекал, а також трамвайні та залізничні колії. Найпростіший приклад сплайнів — ламані.

Більшість диференціальних рівнянь, котрі застосовуються для опису явищ природи та процесів в техніці і хімії, є рівняннями другого порядку. Для коректного відображення інтерпольованої функції в цих рівняннях має бути збережена нерозривність похідних першого і другого порядку. Тому з огляду на економію обчислювальних ресурсів і мінімізацію кількості екстремальних точок інтерполюючого полінома ці вимоги можна задовольнити лише в межах кубічних поліномів, котрі називають кубічними сплайнами, котрі, як доведено [7], є найкращими з функцій, які інтерполюють задану функцію.

Розглянемо задачу інтерполювання функції у=f(x) на відрізку [a;b] за допомогою кубічних сплайнів. Нехай на відрізку [а; b] задано сітку, у вузлах якої відомі значення у_i (і=1,2, ..., п) функції f(x), визначеної на відрізку [a;b]. Будемо шукати функцію S(x), яка задовольняє вимоги:

1) на кожному з відрізків [х_і; х_і+1] , і=1,2,... , n-1 функція S(х) є кубічним поліномом:

2) функція S (х) неперервна на [а; b] разом із своїми похідними до другого порядку включно, тобто

3) у вузлах х_і виконуються рівності

Функцію S(x), що задовольняє ці умови, називають інтерполяційним кубічним сплайном.

Для знаходження 4n-4 невідомих коефіцієнтів сплайна маємо 4n - 6 рівнянь (умови 2, 3). Для коректності не вистачає двох рівнянь, які можна одержати з крайових умов: S"(x₁) = S"(x_п) = 0. Це означає, що на кінцях відрізка інтерполювання сплайн S(x) буде мати нульову кривину. Слід зауважити, що вибір крайових умов можна здійснити й інакше. Зазначимо, що складена система лінійних рівнянь завжди має розв’язок, тобто кубічний сплайн існує для будь-якого набору вузлових точок, що не співпадають.

Задача інтерполювання кубічним сплайном розв’язана і запрограмована в межах практично всіх доступних програмних пакетів.

16) Метод найменших квадратів