Глава 2. Функции многих переменных. Квадратичные формы.

2.1. Квадратичные формы. Критерий Сильвестра. Достаточное условие оптимальности.

С линейными функциями многих переменных студентам пришлось иметь дело в задачах линейного программирования.

При решении различных прикладных задач часто приходится исследовать квадратичные формы [Мальцев, Кремер].

Определение 1. Квадратичной формой L(x_l,x₂,...,x_n) от п переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:

, (1)

Предполагаем, что коэффициенты квадратичной формы а_ij  действительные числа, причем а_ij = а_ji. Матрицу А всегда можно предполагать симметрической (показать это на практике). Действительно, значение L(X) не измениться, если каждый из пары коэффициентов и заменить на . Матрица А = (а_ij) (i, j = = 1, 2, ..., n), составленная из этих коэффициентов, называется матрицей квадратичной формы.

В матричной записи квадратичная форма имеет вид:

L(X) = X'AX, (2)

где X = (x_l, х₂,..., х_n )' — матрица-столбец переменных. В самом деле

.

и эквивалентность формул (1) и (2) установлена.

Пример 2.1. Дана квадратичная форма L(x₁,x₂,x₃) = 2x₁² –12x₁x₂ - 10x₁x₃ +4x₂²-5x₃² . Записать ее в матричном виде.

Решение. Найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, т.е. 2, 4, -5, а другие элементы  половинам соответствующих коэффициентов квадратичной формы. Поэтому

.

Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.

Пусть вектор-столбцы переменных X' = (x₁, x₂,...,x_n)' и Y'= (y₁, y₂, …., y_n)' связаны линейным преобразованием X = CY, где C=(c_ij) (i,j = 1, 2, ...,n) есть некоторая невырожденная матрица n-го порядка. Тогда квадратичная форма после применения преобразования имеет вид

L = X'AX = (CY)'A(CY) = (Y'С')A(СY) = Y'(C'AC)Y.

Итак, при невырожденном линейном преобразовании X = CY матрица квадратичной формы принимает вид:

В = С'АС. (3)

Пример 2.2. Дана квадратичная форма L(x₁,x₂) = 2x₁² –4x₁x₂ – 3x₂². Найти квадратичную форму L(у₁,y₂), полученную из данной линейным преобразованием x_l = 2у₁ - Зу₂, х₂ = у₁ + у₂

Решение. Матрица данной квадратичной формы A = ,

а матрица линейного преобразования C =

Следовательно, по (3) матрица искомой квадратичной формы

=

а квадратичная форма имеет вид L(y₁, у₂) = 13у₁² – 34y₁y₂ + Зу₂². Следует отметить, что при некоторых удачно выбранных линейных преобразованиях вид квадратичной формы можно существенно упростить.

Определение 2. Квадратичная форма

называется канонической (или имеет к анонический или диагональный вид), если все ее коэффициенты а_ij = 0 при ij:

.

а ее матрица является диагональной. Справедлива следующая теорема.

Теорема 1. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.

Пример 2.3. Привести к каноническому виду квадратичную форму методом выделения полного квадрата

L(x₁,x₂,x₃) = x₁² – 3x₁x₂ + 4x₁x₃ + 2x₂x₃ +x₃²

Решение. Вначале выделим полный квадрат при переменной х₁, коэффициент при квадрате которой отличен от нуля:

L(x₁, x₂, x₃) = [x₁² – 2x₁((3·(x₂ – 4x₃)/2)+((3x₂ – 4x₃)/2)²] –

– ((3x₂ – 4x₃)/2)²+2x₂x₃ + x₃² =

= (x₁² – 3·x₂/2+ 2·x₃)² – 9·x₂²/4 + 6·x₂·x₃ – 4·x₃² + 2·x₂·x₃ + x₃² =

= (x₁² – 3·x₂/2+ 2·x₃)² – 9·x₂²/4 + 8·x₂·x₃ – 3·x₃².

Теперь выделяем полный квадрат при переменной х₂, коэффициент при которой отличен от нуля:

L(x₁, x₂, x₃) =

.

'Итак, невырожденное линейное преобразование

приводит исходную квадратичную форму к каноническому виду

L(y, y₂, y₃) = y₁² – 9y₂²/4 + 37·y₃²/9.

Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами, однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств формулируем в виде теоремы.

Теорема 2 (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы в каноническом виде не зависит от способа приведения формы к этому виду.

Например, квадратичную форму L в примере 2.3 можно было привести к виду

L(y, y₂, y₃) = 37y₁²/4 + y₂²  y₃²,

применив невырожденное линейное преобразование

.

Как видим, число положительных и отрицательных коэффициентов (соответственно два и один) сохранилось.

Следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.

Определение 3. Квадратичная форма L(х₁,х₂,...,х_n) называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,

L(х₁,х₂,...,х_n) > 0 (L(х₁,х₂,...,х_n) < 0).

Так, например, квадратичная форма

L₁ = 3x₁² + 4x₁² + 9x₃²

является положительно определенной, а форма

L₂ = 10x₁² + 2x₁x₂  5x₂²

— отрицательно определенной.

Нарисуем трехмерный график (пространственную форму) отрицательно-определенной квадратичной формы.

Рис.1. График отрицательно-определенной формы.

Теорема 3. Для того чтобы квадратичная форма L = Х'АХ была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения i, матрицы А были положительны (отрицательны).

В ряде случаев для установления знакоопределенности квадратичной формы удобнее бывает применить критерий Сильвестра.

Теорема 4 (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е ₁> 0, ₂> 0,…, _n>0, где

.

Следует отметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака "минус" для минора первого порядка.

Доказательство. При n=1 теорема верна, так как форма имеет в этом случае вид ах² и поэтому положительно определена тогда и только тогда, если а>0. Будем поэтому доказывать теорему для случая n неизвестных, предполагая, что для квадратичных форм от n  1 неизвестных она уже доказана.

Сделаем сначала следующее замечание:

Если квадратичная форма L с действительными коэффициентами, составляющими матрицу A подвергается невырожденному линейному преобразованию с действительной матрицей Q, то знак определителя квадратичной формы (т.е. определителя ее матрицы) не меняется.

Действительно, после преобразования мы получаем квадратичную форму с матрицей Q^ТAQ, однако, ввиду |Q^Т| = |Q|,

Q^ТAQ  = Q^ТAQ=AQ²,

т. е. определитель |А| умножается на положительное число.

Пусть теперь дана квадратичная форма

Ее можно записать в виде

, (4)

где  будет квадратичной формой от n1 неизвестных, составленной из тех членов формы L, в которые не входит неизвестное х_n.

Главные миноры формы  совпадают, очевидно, со всеми, кроме последнего, главными минорами формы L.

Необходимость. Пусть форма L положительно определена. Форма  также будет в этом случае положительно определенной: если бы существовали такие значения неизвестных х₁, х₂, …, х_n-1, не все равные нулю, при которых форма  получает не строго положительное значение, то, полагая дополнительно х_n = 0, мы получили бы, ввиду (4), также не строго положительное значение формы L, хотя не все значения неизвестных x₁, х₂, ... , x_n-1, х_n равны нулю. Поэтому, по индуктивному предположению, все главные миноры формы , т. е. все главные миноры формы L, кроме последнего, строго положительны. Что же касается последнего главного минора формы L, т. е. определителя самой матрицы А, то его положительность вытекает из следующих соображений: форма L, ввиду ее положительной определенности, невырожденным линейным преобразованием приводится к нормальному виду, состоящему из n положительных квадратов. Определитель этого нормального вида строго положителен, а поэтому ввиду сделанного выше замечания положителен и определитель самой формы L.

Достаточность. Пусть теперь строго положительны все главные миноры формы L. Отсюда вытекает положительность всех главных миноров формы , т. е., по индуктивному предположению, положительная определенность этой формы. Существует, следовательно, такое невырожденное линейное преобразование неизвестных х₁, х₂, ... , х_n-1, которое приводит форму  к виду суммы n-1 положительных квадратов от новых неизвестных у₁, у₂, ... , у_n-1. Это линейное преобразование можно дополнить до (невырожденного) линейного преобразования всех неизвестных x_l, x₂, ..., х_n, полагая х_n= у_n. Ввиду (4) форма L приводится указанным преобразованием к виду

; (5)

точные выражения коэффициентов b_in для нас несущественны. Так как

,

то невырожденное линейное преобразование

,

,

приводит, ввиду (5), форму L к каноническому виду

. (6)

Для доказательства положительной определенности формы L остается доказать положительность числа с. Определитель формы, стоящей в правой части равенства (6), равен с. Этот определитель должен, однако, быть положительным, так как правая часть равенства (6) получена из формы L двумя невырожденными линейными преобразованиями, а определитель формы L был, как последний из главных миноров этой формы, положительным.

Доказательство теоремы закончено.

Пример 2.4. Доказать, что квадратичная форма L = 13x₁²  6x₁x₂ + 5x₂² является положительно определенной.

Решение. Первый способ. Матрица А квадратичной формы имеет вид

A =

Для матрицы А характеристическое уравнение

.

Решая уравнение, найдем ₁ = 14, ₂ ⁼ 4. Так как корни характеристического уравнения матрицы А положительны, то на основании приведенной теоремы квадратичная форма L — положительно определенная.

Второй способ. Так как главные миноры матрицы А

положительны, то по критерию Сильвестра данная квадратичная форма L положительно определенная.

Нарисуем трехмерный график (пространственную форму) нашей квадратичной формы L = 13x₁²  6x₁x₂ + 5x₂²

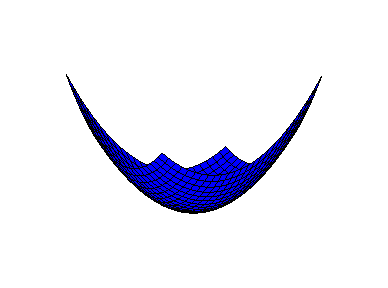
Рис.2. График положительно-определенной формы.

Таким образом, график положительно-определенной квадратичной формы имеет такой вид. Он ограничен областью определения, имеющей вид прямоугольника. На самом деле трехмерный график неограничен.

Определение 4.

Квадратичная форма называется:

1. положительно определенной, если L(X)>0 для всех X0;

2. положительно полуопределенной, если L(X)0, для X и  X0 такое, что L(X)=0.

3. отрицательно определенной, если (–L(X)) есть положительно определенная квадратичная форма;

4. отрицательно полуопределенной, если (–L(X)) – положительно полуопределенная квадратичная форма;

5. неопределенной – в остальных случаях.

Теорема 5 (Необходимые и достаточные условия положительной (отрицательной) определенности квадратичной формы):

1. Квадратичная форма L(X) является положительно определенной , когда значения всех угловых главных миноров матрицы А положительны (матрица А – называется положительно определенной матрицей).

2. Квадратичная форма L(X) является отрицательно определенной , когда значение к-го углового главного минора матрицы А имеет знак (А–отрицательно определенная матрица).

3. Квадратичная форма L(X) является положительно полуопределенной , когда А – вырожденная матрица и все ее главные миноры неотрицательны (А – положительно полуопределенная матрица).