Лабораторная работа № 4

Тема: Приближенное решение алгебраического/трансцендентного уравнения различными методами.

Цель: научиться применять методы локализации и уточнения корня для решения алгебраических и трансцендентных уравнений с учетом условий применимости указанных методов.

Содержание работы по вариантам:

№ варианта	Содержание задания	Метод решения
1		Решить уравнение методом простой итерации с точностью ,
2		Решить уравнение методом касательных с точностью ,
3		Решить уравнение методом половинного деления с точностью ,
4		Решить уравнение методом простой итерации с точностью ,
5		Решить уравнение методом половинного деления с точностью ,
6		Решить уравнение методом простой итерации с точностью ,
7		Решить уравнение методом касательных с точностью ,
8		Решить уравнение методом половинного деления с точностью ,
9		Решить уравнение методом простой итерации с точностью ,
10		Решить уравнение методом касательных с точностью ,

Порядок выполнения работы:

1. проанализировать уравнение, определить его тип;

2. выяснить область определения функций, входящих в уравнение;

3. определить максимально возможное число корней уравнения;

4. указать приближенное значение корня на отрезке локализации, найденное графическим методом;

5. проверить условие применимости требуемого метода, если это необходимо;

6. решить уравнение указанным методом;

7. осуществить проверку найденного решения.

Контрольные вопросы:

1. Уравнение, корень уравнения, алгебраические и трансцендентные уравнения. Примеры алгебраических и трансцендентных уравнений.

2. Сформулируйте теоремы о свойствах непрерывных функций, проиллюстрируйте их с помощью графиков.

3. Методы уточнения корня.

4. Метод половинного деления.

5. Достоинства и недостатки метода половинного деления.

6. Метод касательных (метод Ньютона).

7. Перечислите требования, которым должна удовлетворять функция 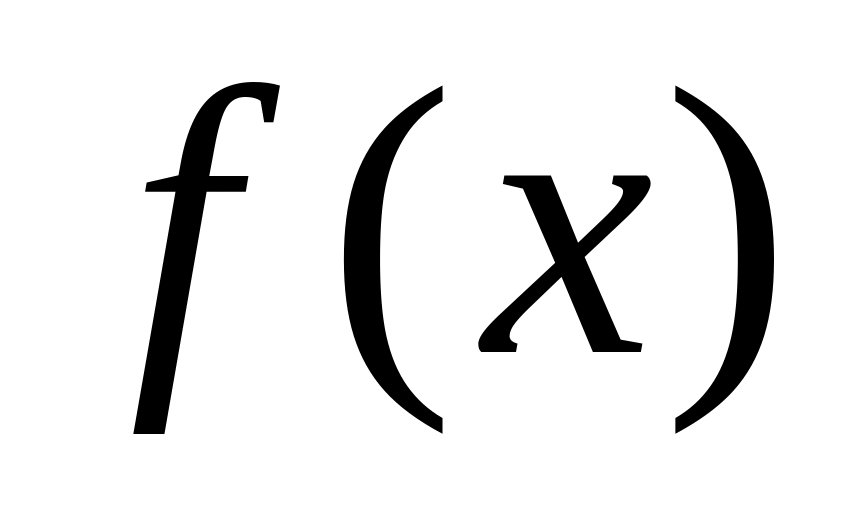для решения уравнения методом касательных.

8. Типы расположения дуги кривой функции , удовлетворяющей требованиям метода касательных.

9. Геометрическая иллюстрация метода касательных.

10. Вывод формулы для метода касательных.

11. Каким образом выбирается начальное приближение при решении уравнения методом касательных.

12. Сформулируйте условие сходимости метода Ньютона.

13. Запишите условие прекращения итерационного процесса по методу Ньютона.

14. Метод последовательных приближений (метод простой итерации).

15. Условия применимости метода простой итерации.

16. Геометрическая иллюстрация метода последовательных приближений для решения уравнения с одной переменной.

17. Связь метода Ньютона с методом простой итерации.

18. Вычисление корня любой степени методом простой итерации.