3.2 Отсев грубых погрешностей на примере
Для выборки, представленной в таблице 1.1 (n = 25), необходимо провести отсев грубых погрешностей.
Отсев грубых погрешностей методом максимального относительного отклонения:
а) вычисляем среднее значение выборки:
б) вычисляем среднеквадратичное отклонение:
в) определяем статистику для крайних (наибольшего или наименьшего) элементов выборки:
-
для наибольшего элемента выборки
-
для наименьшего элемента выборки
г) определяем табличное значение статистики (Приложение ) при доверительной вероятности q= 0,95 или уровне значимости 0,05
д) сравниваем найденные значения статистики с табличным значением
2,06
< 2,62 - наблюдение отсеивать нельзя
1,42
< 2,62 - наблюдение отсеивать нельзя
Отсев грубых погрешностей для выборок малых объемов. Возьмем выборку n=10 и представим ее в виде вариационного ряда (таблица 3.1).
Таблица 3.1 – Значения выборки
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
xi |
0,15 |
0,34 |
0,99 |
1,11 |
1,57 |
2,23 |
2,34 |
2,34 |
2,48 |
4,15 |
По формуле 3.5 вычислим значение τ. Для этого необходимо вычислить
среднеквадратичное отклонение по формуле 3.2.
Данные
необходимые для вычисления
приведем
в таблице 3.2.
Таблица 3.2 - Данные для вычисления
№ |
xi |
|
|
1 |
0,15 |
-1,62 |
2,624 |
2 |
0,34 |
-1,43 |
2,045 |
3 |
0,99 |
-0,78 |
0,608 |
4 |
1,11 |
-0,66 |
0,436 |
5 |
1,57 |
-0,2 |
0,04 |
6 |
2,23 |
0,46 |
0,212 |
7 |
2,34 |
0,57 |
0,325 |
8 |
2,34 |
0,57 |
0,325 |
9 |
2,48 |
0,71 |
0,504 |
10 |
4,15 |
2,38 |
5,664 |
∑ |
17,7 |
|
12,783 |
Определяем статистику для крайних (наибольшего или наименьшего) элементов выборки по формуле:
-
для наибольшего элемента выборки
- для наименьшего элемента выборки
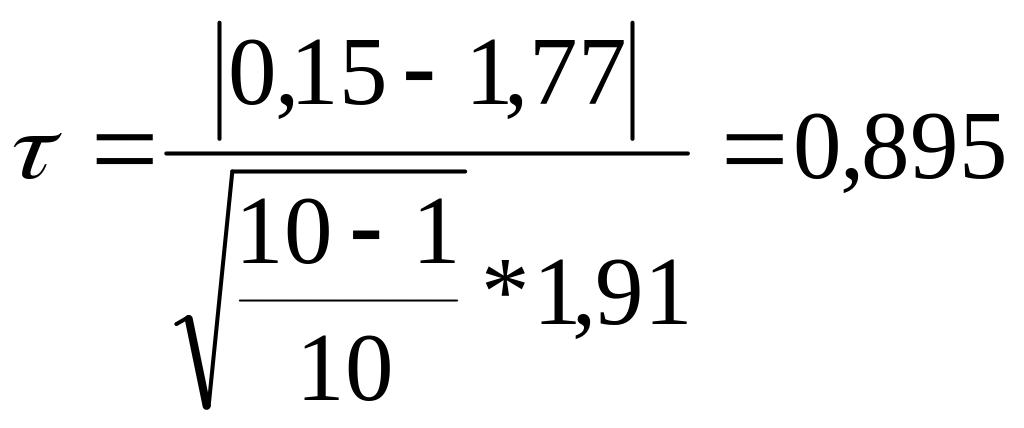
г) определяем табличное значение статистики (Приложение ) при доверительной вероятности q= 0,95 или уровне значимости 0,05
д) сравниваем найденные значения статистики с табличным значением
1,315
< 2,29 - наблюдение отсеивать нельзя
0,895
< 2,29 - наблюдение отсеивать нельзя.
3 Отсев грубых погрешностей для выборок большого объема (использование таблиц распределения Стьюдента).
Для выборки, представленной в таблице 1.1 (n = 20), необходимо провести отсев грубых погрешностей с использованием таблиц распределения Стьюдента.
Определяем среднее значение для данной выборки, отклонение от среднего для каждого члена выборки и среднеквадратичное отклонение. Все результаты вычисления сведем в таблицу 3.3.
Таблица
3.3 - Данные для вычисления
,
№ |
|
|
|
№ |
|
|
|
1 |
9,81 |
5,734 |
32,879 |
11 |
6,72 |
2,644 |
6,991 |
2 |
2,34 |
-1,736 |
3,0137 |
12 |
5,15 |
1,074 |
1,153 |
3 |
6,55 |
2,474 |
6,121 |
13 |
0,34 |
-3,736 |
13,958 |
4 |
0,15 |
-3,926 |
15,413 |
14 |
2,23 |
-1,846 |
3,408 |
5 |
8,63 |
4,554 |
20,739 |
15 |
4,85 |
0,774 |
0,599 |
6 |
7,11 |
3,034 |
9,205 |
16 |
5,01 |
0,934 |
0,872 |
7 |
1,57 |
-2,506 |
6,280 |
17 |
4,15 |
0,074 |
0,005 |
8 |
2,34 |
-1,736 |
3,014 |
18 |
1,11 |
-2,966 |
8,797 |
9 |
5,55 |
1,474 |
2,173 |
19 |
2,48 |
-1,596 |
2,547 |
10 |
0,99 |
-3,086 |
9,523 |
20 |
4,44 |
0,364 |
0,132 |
∑ |
81,52 |
|
146,824 |
||||
Из таблицы 3.3 выберем наблюдения, имеющие наибольшее и наименьшее отклонения:
Вычисляем
τ
для
по
формуле (3.7).
По таблице (Приложение ) находим процентные точки t - распределения Стьюдента для 5% и 0,1% и соответствующем объеме выборки (n=20).
t(0,1; 18) = 3,6105 t(5; 18) = 1,7341
Вычисляем
соответствующие точки критического
значения
по
формуле (3.8) и (3.9):
Полученные
сравниваем с
и
делаем соответствующие выводы.
Тогда, для максимального значения выборки выполняется условие
1,6491<2,061<2,825 – решение об отсеве данного наблюдения принимается экспериментатором.
Для минимального значения выборки выполняется условие 1,412<1,6491 – наблюдение отсеивать не нужно.