7.7. Косинус фи и коэффициент мощности

Обычно для систем электроснабжения до 1000 В используют термин "косинус "фи" , а для систем электроснабжения напряжением выше 1000 В используют термин «коэффициент мощности».

Коэффициент мощности или "косинус "фи"  определяется по формулам:

, ,

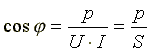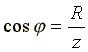где р – мгновенная активная мощность, U – напряжение, I – ток, S – мгновенная полная мощность, R – активное сопротивление, Z – полное сопротивление.

  Коэффициент  мощности  является одной из важнейших характеристик электротехнических устройств. Смысл угла фи - угол между вектоpами напpяжения и тока. Смещение их фаз. Если нагpузка активная (лампочка накаливания, тэн и т.п.) то угол pавен нулю, мощность pавна пpоизведению тока на напpяжение. А вот если нагpузка pеактивная, напpимеp конденсатоp или индуктивность, то угол равен 90 градусов, косинус равен нулю, смещение фаз pовно на четвеpть цикла и мощность равна нулю. Хотя ток идет и напpяжение есть.

В pеальном случае имеет место нечто сpеднее, например активная нагpузка с добавкой pеактивности. Hапpимеp, типичный случай индуктивной нагpузки - лампы с дpосселями. В pезультате ток во всей цепи отстает от напpяжения, возникает тот самый угол фи и его косинус, и для тех же скажем 250 Вт активной мощности ток должен быть уже не 1А а 2А. Отсюда и пpоблемы - для пеpедачи той же мощности (на освещение, на двигатель и т.п.) система электроснабжения должна быть pассчитана на существенно больший ток.

Чтобы не происходило пустой траты электроэнергии, параллельно в сеть подключают конденсаторы, которые опережают по фазе активную составляющую и компенсируют индуктивность своей емкостной характеристикой. Косинус фи приближается к единице именно тогда, когда емкостная мощность приравнивается к индуктивной. В этом случае меньше и напрасных потерь электрической энергии.

7.8. Поперечная компенсация (ппк)

Работы большинства потребителей переменного тока связана с потреблением реактивной мощности (Q). Реактивная мощность, загружая обмотки двигателей, трансформаторов и провода линий, увеличивает потери энергии (_ΔW).

Рассмотрим коэффициент мощности: он обозначается как «cos», либо как «Км».

(7.1)

где P_t – активная (полезная мощность) в момент времени t; Q_t – реактивная мощность в момент времени t; S_t – полная мощность в момент времени t.

Угол φ – это угол между током и напряжением. Активная и реактивная мощность определяется следующим образом:

, (7.2)

. (7.3)

Полная мощность определится следующим образом:

(7.4)

Основная цель поперечной (параллельной) компенсации состоит в повышении коэффициента мощности.

Коэффициент мощности на шинах ТП равен Км (cos φ) = 0,75 / 0,85. Обычно принимается равным 0,82. В наше время по участку Км должен быть не ниже 0,92 / 0,95.

Рассмотрим схему замещения и векторную диаграмму поперечной компенсации для случая однофазной поперечной компенсации.

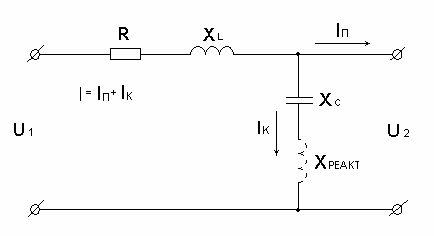
Рис. №7.11 Схема замещения поперечной компенсации

На схеме (рис.168):

R – активное сопротивление;

Х_L – реактивное (реактивное) сопротивление;

Х_С – емкостное сопротивление поперечной компенсации;

U₁ – напряжение холостого хода;

U₂ – напряжение потребителя до ППК;

U₂’ – напряжение потребителя после ППК;

Х_реакт – сопротивление реактора в цепи поперечной компенсации;

I_П – ток потребителя;

I_К – ток ветви компенсации;

I – общий ток.

До компенсации I = I_П , так как не было контура Х_С. После компенсации I = I_П + I_К.

До установки ППК потеря напряжения определится как

, (7.5)

или

. (7.6)

На рис. 169 приведена векторная диаграмма токов и напряжений до установки ППК.

После установки ППК потеря напряжения определится как

, (7.7)

или

. (7.8)

Рис. №7.12 Векторная диаграмма токов и напряжений до установки ППК

На рис. 7.13 приведена векторная диаграмма токов и напряжений после установки ППК.

Рис. №7.13 Векторная диаграмма токов и напряжений после установки ППК

Как видно из векторной диаграммы, следствием применения поперечной компенсации является уменьшение потерь напряжения.

_ΔU’ < _ΔU.

Однако цель компенсации – увеличение коэффициента мощности, действительно, судя по диаграммам

cos ’ > cos .

Из выражения видно, что подбором можно свести потерю напряжения (_ΔU) к нулю, или даже дать ей отрицательное значение. Емкость конденсаторной батареи влияет на величину I_К, а эта величина влияет, в свою очередь, на _ΔU).

Включение емкости создает условие для резонанса, для того, чтобы не допустить резонанса, последовательно с емкостной батареей Х_к (Х_с) включают реактор (Х_реакт).

Его индуктивность подбирают таким образом, чтобы индуктивность для 3-ей гармоники была равна емкостному сопротивлению батареи.

Х_реакт3 = Х_к3

ƒ₃ = 150 Гц

т.е. создается резонанс для 3-ей гармоники, для того, чтобы ликвидироать резонанс на основной частоте (50 Гц).

Условие резонанса:

, (7.9)

где ω – угловая частота, L – индуктивность, С – емкость.

ω = 2πƒ, (7.10)

где f – частота.

Если ƒ = 150, тогда

2π ∙ 150 ∙ L = 1/(2π ∙ 150 ∙ С)

Тогда для нормальной частоты (1-я гармоника) Х_{реактора1} = Х_{реактора3} / 3, а Х_с1 = 3Х_с3, поэтому общее сопротивление поперечной компенсации будет иметь емкостный характер. А с учетом Х_реакт3 = Х_с3 можно записать, что

Х_реакт1 = Х_с1 / 9.

Однако включение реактора уменьшает емкостный эффект конденсаторной батареи (индуктивность реактора компенсирует емкость).

Для обеспечения сопротивления емкостной батареи, необходимого по условиям компенсации реактивной мощности, ее сопротивление должно быть больше на значение сопротивления реактора, т.е.

Х_ппк1 = Х_с1 – Х_реакт1 = Х_с1, тогда

Х_с1 = 1,125 Х_ппк1,

где ппк – поперечная компенсация (параллельная), Х_ппк – сопротивление ппк.

Установка ППК может быть установлена на тяговой подстанции, на перегоне (на посту секционирования). Эффект от ППК будет больше, если установить ППК на самой нагрузке, т.е. на ЭПС, но это не делается вследствие отсутствия места на ЭПС.

Рассмотрим компенсацию (ППК) для 2-х плеч одной тяговой подстанции переменного тока (рис.7.14).

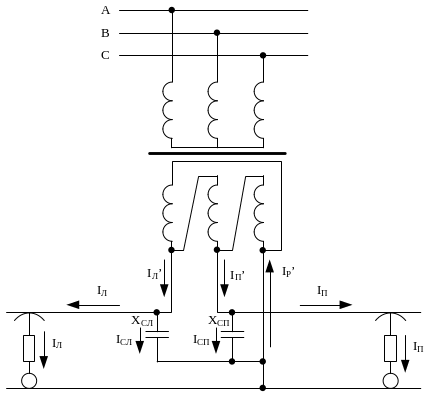
Рис. №7.14 Поперечная компенсация для 2-х плеч тяговой подстанции переменного тока

Токовые нагрузки по плечам постанции после установки ППК будут равны:

I_Л’= I_Л + I_СЛ, (7.11)

I_П’= I_П + I_СП. (7.12)

Потерю напряжения в данном случае уменьшает батарея, включенная в «свою» фазу и в «соседнюю» фазу. При этом влияние емкости «своей» фазы в 4 раза больше влияния емкости «соседней» фазы.

Рассмотрим векторную диаграмму для данной схемы (рис.5).

Пунктиром обозначены векторы потерь напряжения до установки ППК, т.е. при отсутствии векторов I_сл и I_сп. Жирными линиями обозначены вектора компенсации потерь напряжения, т.е. после установки ППК.

На рис.5 величина реактивного сопротивления (Х) равна:

Х = Х_S’ + X_T, (7.13)

где Х_S’ – сопротивление энергосистемы, приведенное к напряжению на вторичной стороне подстанции, X_T – то же трансформатора.

Рис. №7.15 Векторная диаграмма поперечной компенсации для 2-х плеч тяговой подстанции переменного тока