55.Понятие лямбда-исчисления.
Ля́мбда-исчисле́ние (λ-исчисление) — формальная система, разработанная американским математиком Алонзо Чёрчем, для формализации и анализа понятия вычислимости.
λ-исчисление может рассматриваться как семейство прототипных языков программирования. Их основная особенность состоит в том, что они являются языками высших порядков. Тем самым обеспечивается систематический подход к исследованию операторов, аргументами которых могут быть другие операторы, а значением также может быть оператор. Языки в этом семействе являются функциональными, поскольку они основаны на представлении о функции или операторе, включая функциональную аппликацию и функциональную абстракцию. λ-исчисление реализовано Джоном Маккарти в языке Лисп. Вначале реализация идеи λ-исчисления была весьма громоздкой. Но по мере развития Лисп-технологии (прошедшей этап аппаратной реализации в виде Лисп-машины) идеи получили ясную и четкую реализацию.
56. Операции лямбда-исчисления.
Аппликация и абстракция
В основу λ-исчисления положены две фундаментальные операции:
Аппликация (лат. application — прикладывание, присоединение) означает применение или вызов функции по отношению к заданному значению. Её обычно обозначают
,
где 
—
функция, а 
—
аргумент. Это соответствует общепринятой
в математике записи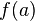 
,
которая тоже иногда используется,
однако для λ-исчисления важно то,
что
трактуется
как алгоритм,
вычисляющий результат по заданному
входному значению. В этом смысле
аппликация
к
может
рассматриваться двояко: как результат
применения
к
,
или же как процесс вычисления
.
Последняя интерпретация аппликации
связана с понятием β-редукции.Абстракция или λ-абстракция (лат. abstraction — отвлечение, отделение) в свою очередь строит функции по заданным выражениям. Именно, если
—
выражение,свободно содержащее 
,
тогда запись 
означает: 
функция
от аргумента
,
которая имеет вид 
,
обозначает функцию 
.
Таким образом, с помощьюабстракции можно
конструировать новые функции. Требование,
чтобы
свободно
входило в 
,
не очень существенно — достаточно
предположить, что 
,
если это не так.
β-редукция
Поскольку
выражение 
обозначает
функцию, ставящую в соответствие
каждому
значение 
,
то для вычисления выражения
,
в
которое входят и аппликация и абстракция,
необходимо выполнить подстановку числа
3 в терм
вместо
переменной
.
В результате получается 
.
Это соображение в общем виде записывается
как
и
носит название β-редукция.
Выражение вида 
,
то есть применение абстракции к некому
терму, называется редексом (redex).
Несмотря на то, что β-редукция по сути
является единственной
«существенной» аксиомой λ-исчисления,
она приводит к весьма содержательной
и сложной теории. Вместе с ней λ-исчисление
обладает свойством полноты
по Тьюрингу и,
следовательно, представляет собой
простейший язык
программирования.
57. Чистое лямбда-исчисление.
Чистое λ-исчисление
Это простейший из семейства прототипных языков программирования, чистое λ-исчисление, термы которого, называемые также объектами («обами»), или λ-термами, построены исключительно из переменных применением аппликации и абстракции. Изначально наличие каких-либо констант не предполагается.