Билет № 5 Вопрос №1

Решение

Для определения момента инерции составим дифференциальное уравнение вращательного движения:

I_z · ε = ΣM_K, где

I_z – момент инерции тела

ε – угловое усковение

ΣM_K – суммарный момент всех действующих сил

Условие ускорения : ε = dω/dt

Подставим значение условного ускорения в дифференциальное уравнение:

I_z · (dω/dt) = ΣM_K

Произведём деление переменных и проинтегрируем полученное выражение:

I_z · dω = M · dt

I_z∫^w₀ dω = 16∫^t₀ tdt; I_z(ω – 0) = 8(t² – 0) => I_z · ω = 8t²

I_z = 8t²/ω

I_z = (8 · 3²)/2 = 36 кг · м²

Ответ 36 кг · м²

Вопрос №2

Решение

Схема соединения эвольвентного шлицевого соединения

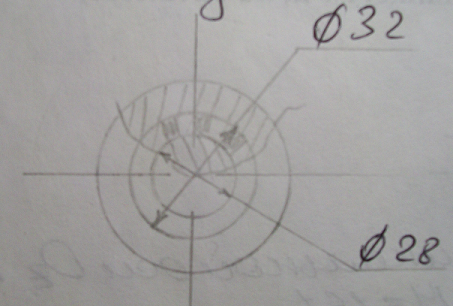
По ГОСТ 6033- 80 выбираем эвольвентное шлицевое соединение с модулем m = 2 мм, D = 32 мм, z = 14, [σ_см] = 30...60 МПа.

Проверяем соединение на смятие

σ_см = 2 · Т_к / ( d_cp · b · l · z · ψ ) ≤ [σ_см], где :

Т_к = 0,4 кН · м – вращающий момент

d_cp = m · z = 2 · 14 = 28 мм – средний диаметр соединения

b и l – соответственно высота и длина поверхности контакта шлица,

l = 55 мм, b = m · Θ = 2 · 0,9 = 1,8 где

Θ – при центрировании по наружному диаметру

ψ – 0,7 – 0,8 – коэффициент учитывающий неравномерность распределения давления в соединении, принимаем ψ = 0,75

σ_см = 2 · 0,4 · 10^-3/ 28 · 10^-3 · 14 · 1,8 · 10^-3 · 55 · 10^-3 · 0, 75 = 27, 48 МПа ≤ [σ_см]

= 45 МПа

Билет № 6 Вопрос № 1

Р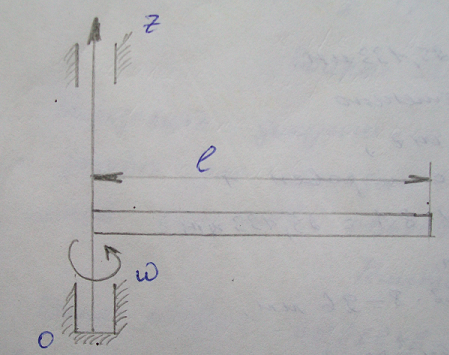 ешение

Для определения момента сопротивления составим дифференциальное уравнение вращения стержня вокруг оси oz :

I_cε = M_z;

M_z = - M_c

где I_c – момент инерции стержня

ε – угловое ускорение

Момент инерции стержня определяется по формуле:

I_c = ml²/3;

Угловое ускорение является первой производной от угловой скорости, т.е.

ε = dω/dt

Подставляем полученную формулу в уравнение вращения:

(ml²/3) · dω/dt = - M_c

Полученное уравнение является дифференциальным и для его решения, произведём разделение переменной :

(ml²/3) · dω = M_c · dt

Проинтегрируем полученное уровнение

ml²/3 ∫⁰_w dω = M_c ∫^t₀ dt

(ml²/3) · (0 – ω) = M_c (t – 0)

Подставим данные задания и получим:

M_c = (ml² · ω)/3t

M_c = 3 · 1² · 24/ 3 · 4 = 6 Н · м

Ответ М_с = 6 Н · м

Вопрос № 2

Решение

Определим расчётный шаг червяка

Р = m · π , где m - модуль зацепления

Р = 8 · 3,14 = 25, 133 мм

Ход витка червяка определяем по выражению:

Р_z1 = P · z = π · m · z₁

z₁ – число заходов витка червяка

P_z1 = 25,133 · 1 = 25,133

h_at = m = 8 мм

h_ft = 1,2 · m = 9,6 мм

Диаметр делительной окружности червяка

d_t = q · m

q – коэффициент диаметра червяка, = 12,5

d_t = 12,5 · 8 = 100 мм

Делительный угол подъёма червяка

γ = arctg (z₁/q) = arctg (1/12,5) = 4^o

Диаметр вершин витков червяка

d_a1 = d₁ + l_a1 = q · m + z · m = m (z+q) = 8 · (12,5 + 2) = 116 мм

Диаметр впадин:

d_f1 = d_a1 – 2h · f₁ = m · g – 2 · 1,2m = m ( q – 2,4) = 8 · (12,5 – 2,4) = 80,8 мм

b₁ = m (11 + 0,06 · z_в)

z_k – число зубъев колеса

z_k = z₁ · U = 1 · 50 = 50

U – передаточное число передачи U = 50.

b₁ = 8 (11 + 0,06 · 50) = 112мм.

Определим делительный диаметр колеса:

d_z = m · z_k = 8 · 50 = 400мм.

Диаметр вершин зубъев

d_a = d_z + 2h_z = m · z_k + 2m = m (z_k + 2) = 8 · ( 50 + 2 ) = 416 мм.

d_t = m ( z_k – 2,4) = 8 · (50 – 2,4) = 380,8 мм

Наибольший диаметр червячного колеса

d_am = (6 · m)/(z₁ + 2) + d_a = (6 · 8)/(1 + 2) + 416 = 432мм

Ширина венца червячного колеса:

b₂ = 0,75 d_a1 = 0,75 · 116 = 87 мм

Межосевое расстояние передачи определим

a_w = (m/2) · (q + z₂) = 8/2 · ( 12,5 + 50 ) = 250 мм