Билет № 1 Вопрос № 1

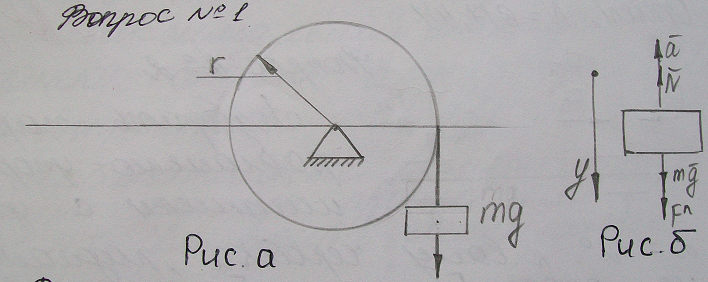
Дано:

m = 60 кг

φ = 60t²

r = 0,4 м

N - ?

Решение

Для определения натяжения нити смотрим кинематическое равновесие блока. Для сохранения равновесия системы вращающейся барабан заменяем силой N, которая представляет собой искомую величину силы натяжения нити. Для системы сил изображаем ( рис. б) принцип Доломбера:

ΣF¯ + Fⁿ¯ = 0 (1)

Применительно для нашего случая можно записать так:

ΣF_y¯ + F_yⁿ¯ (2)

Тогда:

F_yⁿ – mg – N = 0;

N = F_y^-n + mg

где N – натяжение нити, Fⁿ = сила инерции.

Определяем величину силы инерции входящей в уравнение (2)

F_n = - ma¯ (3)

и в проекции на ось y Fⁿ_y = ma_y (4)

Ускорение, с которым груз поднимается, равно тангенциальной составляющей ускорения ε барабана.

a_y = a_τ = ε_r (5)

где ε – угловое ускорение барабана.

Определяем ε · ε = φ, φ = ω = 0,6t · 2 = 1,2t => в (5), a_y = 1,2r

φ = ε = 1,2 рад/с² (6)

Подставляем (6) в(5), a_y = 1,2r

(5) в (4), F_y = 1,2r·m

Определив силу инерции, мы можем определить силу силу натяжения нити:

N = 1,2r · m + mg = m(1,2r + g)

N = 60 · ( 1,2 · 0,4 + 9,81) = 617,4Н

О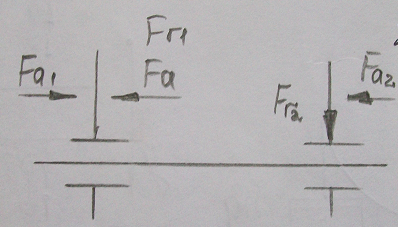 твет 617,4Н

Вопрос№2

Решение

1. Примем радиально-упорные подшипники серии 7208. Данные берём по справочнику: d = 40 мм, D = 80 мм, T = 20 мм, c = 1,5 мм, С = 46,5кН,

l = 0,383

2) Найдём осевые составляющие реакции S₁₄S₂

Для радиально-упорных подшипников S = 0,83 · l · F_r. Тогда:

S₁ = 0,83 · l · F_r1, S₁ = 0,83 · 0,383 · 1,6 = 0,509 кН

S₂ = 0,83 · l · F_r2, S₂ = 0,83 · 0,383 · 1,4 = 0,445 кН

3. Найдём расстояние а от торца кольца подшипника, на котором находится точка приложения реакций

a = 0,5T + (c/3)(d + D) = 0,5 · 20 + 1,5/3 (40 + 80) = 70 мм

4) Найдём эквивалентные силы Р_э:

Р_э = (х F_r + VF_a) · K_б · К_т,

К_т = 1, где х, у – находим по таблице

x = 1; y = 0

т.к. (F_a/VF₂) < l₁,

Р_э1 = 1 · 1,6 + 1 · 0,509) · 1 · 1,3 = 2,74 кН

Р_э2 = (1 · 1,4 +1 · 0,445) · 1 · 1,3 = 2, 398 кН

Расчётную долговечность ά_h будем находить по максимальной эквивалентной нагрузке Р_э

ά_h = 10⁶/(60 · n) · (C/P_э)ⁿ,где n = 3,33

ά_h = 10⁶/ (60 · 940) · (46,5/2,74)^3,33 = 0,22 · 10⁶ = 220000ч.

Что больше максимально расчётной ά_h = 10000ч. Значит подшипники выбраны верно, это серия 7208.

Билет № 2 Вопрос № 1

Решение

Д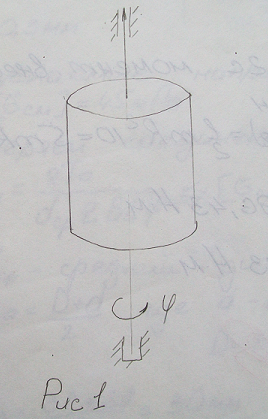 ля определения главного момента внешних сил действующих на тело воспользуемся уравнением динамики вращательно движения твёрдого тела.

I_zε = ΣM_z (1)

ε – угловое ускорение

Момент инерции тела вычисляем по формуле : I_z = 0,5 mR² (2)

Определяем угловое ускорение которое ровняется производной от φ, т.е.

ε = ¨φ (3)

φ˙ = ω = (t³ – t²)` = 3t² – 2t (4)

¨φ = ε = ω` (3t² – 2t) = 6t – 2 (5)

Подставим (5) и (2) в уравнение (1)

ΣM_z = 0,5 mR²(6t – 2)

Для времени t = 2c момент внешних сил будет равен:

ΣM_z = 0,5mR² · (6 · 2 – 2)= 0,5mR² · 10 = 5mR²

ΣM_z = 60 · (1,41)² · 5 = 596,43 Н · м

Ответ : ΣM_z = 596,43 Н · м

Вопрос № 2

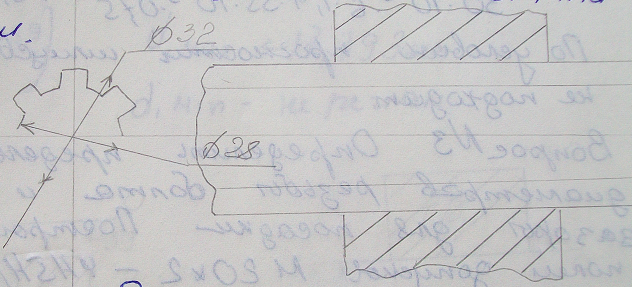
Решение:

1. Выбираем прямобочное шлицевое соединение легкой серии d = 28; D = 32; z = 6; f = 0,3мм.

2. Допускаемые напряжения [σ_см] = 45МПа

3. Проверяем соединение на смятие:

σ_см = 2Т_о/(d_cp · z · B · L · φ) ≤ [σ_см], где

d_cp – средний диаметр соединения

d_cp = (D + d)/2 , где

d – Внутренний диаметр соединения, 28 мм

D – Наружный диаметр шлицевого соединения, 32 мм

d_cp =(32 + 28)/2 = 30 мм

z = 6, число шлицов

b и l – соответственно высота и длина поверхности контакта шлица

Высота поверхности определяется выражением:

B =(D – d)/2 – 2f, где

f – величина фаски, равна 0,3 мм

B = 32 – 28/2 – 2 · 0,3 = 1,4 мм.

φ = 0,75 , [σ_см] = 45 МПа – допустимое напряжение на боковых поверхностях шлица.

σ_см= 2 · 0,4 · 10³/(30 · 10^-3 · 6 · 1,4 · 55 · 10^-3 · 0,75) = 76,96 МПа ≥ [σ_см]

По условию прочности шлицевое соединение не подходит.