1.3 Минимизация логических функций
Задача минимизации логических функций – переход от СДНФ к ДНФ с минимумом слагаемых, при этом количество множителей в каждом слагаемом должно быть также минимальным. Иными словами – максимально уменьшить количество переменных и операций в СДНФ.
Упростить функцию можно непосредственно с помощью алгебраических преобразований с использованием логических тождеств, а также используя различные алгоритмы минимизации логических функций.
Рассмотрим алгоритм нахождения минимальной дизъюнктивной нормальной формы с помощью карт Карно.
Карта Карно – графическое представление связей между логическими переменными – представляет собой четырехугольный прямоугольник, разделенный на элементарные квадраты. Каждому квадрату соответствует определенная комбинация всех входных переменных. Обозначения входных переменных записываются сбоку и сверху карты и относятся ко всей строке или столбцу следующих за ними элементарных квадратов. При этом считается, что значения соответствующих входных переменных в этих квадратах равны 1. В каждом квадрате карты Карно записывается значение логической функции, которая изображается этой картой. Число элементарных квадратов в карте Карно равно числу всех возможных наборов входных переменных, т.е. 2n, где n – количество аргументов логической функции.
Карта Карно заполняется по СДНФ. В элементарных квадратах, соответствующих конъюнктивным членам СДНФ, ставятся 1. Заполненная карта Карно используются для нахождения минимальной формы логической функции.
Минимизация базируется на основном свойстве карт Карно, которое состоит в том, что при переходе от одного элементарного квадрата к любому соседнему (по вертикали или по горизонтали) изменяется значение только одной переменной на инверсное. Поэтому математическое выражение контура, охватывающего две соседние единицы, не зависит от одной переменной. Аналогично, математическое выражение контура, охватывающего четыре единицы, не зависит от двух переменных.
Отсюда следуют правила минимизации с использованием карт Карно:
на карте Карно выделяются четырехугольные контуры, охватывающие возможно большее количества единиц. В каждом таком контуре количества единиц должно быть максимально возможным, но кратным степени двойки. Контуры могут пересекаться, причем выделенные таким образом контуры должны охватывать все единицы карты Карно;
МДНФ логической функции получается как дизъюнкция математических выражения для всех контуров (это будут конъюнкции).
Таким образом, получим МДНФ для каждой выходной переменной Y1, Y2, Y3, Y4.
Y1=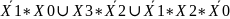
Y2=
Y3=
Y4=
1.4 Разработка функциональной схемы устройства
На основании задания на курсовое проектирование перед разработкой функциональной схемы логического устройства необходимо преобразовать полученную минимизированную логическую функцию к заданному базису И-НЕ.
Преобразование логической функции устройства к заданному базису осуществляется по следующему алгоритму:
двойное инвертирование всего выражения или его части;
применение правила де Моргана над всем выражением или его частями.
Правило де Моргана (закон инверсии):
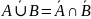
Используя закон двойного отрицания, можно преобразовать закон инверсии в более удобный вид:
Таким образом, получим логические функции в базисе И-НЕ для каждой выходной переменной Y1, Y2, Y3, Y4.
Y1 =
Y2 =
Y3 =
Y4 =
По полученным для каждого разряда выходной функции минимальным формам составляется функциональная схема разрабатываемого устройства. Обозначения логических элементов, применяемых при начертании функциональной схемы, представлены на рисунке 1.
Рисунок 1 – Обозначения логических элементов
Следует отметить, что каждый элемент схемы отражает лишь функциональную связь между входными и выходными переменными.
Составленная функциональная схема вычерчена на отдельном листе «Схема электрическая функциональная» формата А3 с соблюдением стандартов и требований ГОСТа и представлена в графической части курсового проекта.