Билет №6. Представление информации в цифровых автоматах. Преобразование правильных дробей из одной системы счисления в другую.

Перевод правильных дробей из десятичной системы счисления в недесятичную.  Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.

Пример.

Перевести 0.312510 "8" с.с.

    

Результат: 0.312510 = 0.248

Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.

Пример.

Перевести 0.6510 "2" с.с. Точность 6 знаков.

    

Результат: 0.6510   0.10(1001)2

Билет №7. Арифметические операции в позиционных системах счисления: сложение, вычитание, умножение и деление. Примеры.

Сложение.

Пример 1. Сложим числа 15 и 6 в различных системах счисления.

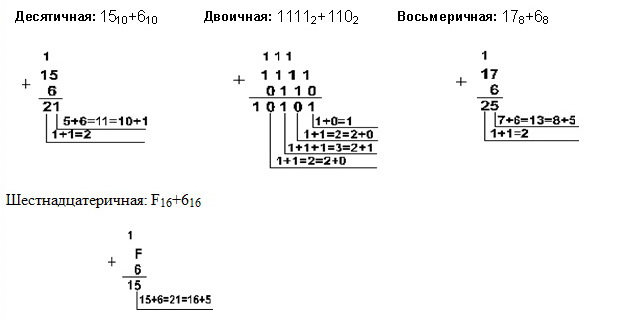
Вычитание. При вычитании цифры вычитаются по разрядам, и если при этом возникает недостаток, то происходит заем в старших разрядах.

Умножение. Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Деление. Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей. Пример 1. Разделим число 30 на число 6.

Билет №8. Системы счисления по основанию 2, 8, 10, 16. Представление целых неотрицательных и отрицательных чисел в ЭВМ. Прямой, обратный и дополнительный коды. Примеры прямого, обратного и дополнительного кодов восьмибитового положительного и отрицательного целого числа. Запишите в десятичной с.с. целое число по его дополнительному коду.

Представление целых чисел в компьютере.

Целые числа являются простейшими числовыми данными, с которыми оперирует ЭВМ. Для целых чисел существуют два представления: беззнаковое (только для неотрицательных целых чисел) и со знаком. Очевидно, что отрицательные числа можно представлять только в знаковом виде. Целые числа в компьютере хранятся в формате с фиксированной запятой.

Представление целых чисел в беззнаковых целых типах.

Для беззнакового представления все разряды ячейки отводятся под представление самого числа. Например, в байте (8 бит) можно представить беззнаковые числа от 0 до 255. Поэтому, если известно, что числовая величина является неотрицательной, то выгоднее рассматривать её как беззнаковую.

Представление целых чисел в знаковых целых типах.

Для представления со знаком самый старший (левый) бит отводится под знак числа, остальные разряды - под само число. Если число положительное, то в знаковый разряд помещается 0, если отрицательное - 1. Например, в байте можно представить знаковые числа от -128 до 127.

Прямой код числа.

Представление числа в привычной форме "знак" - "величина", при которой старший разряд ячейки отводится под знак, а остальные - под запись числа в двоичной системе, называется прямым кодом двоичного числа. Например, прямой код двоичных чисел 1001 и -1001 для 8-разрядной ячейки равен 00001001 и 10001001 соответственно. Положительные числа в ЭВМ всегда представляются с помощью прямого кода. Прямой код числа полностью совпадает с записью самого числа в ячейке машины. Прямой код отрицательного числа отличается от прямого кода соответствующего положительного числа лишь содержимым знакового разряда. Но отрицательные целые числа не представляются в ЭВМ с помощью прямого кода, для их представления используется так называемый дополнительный код.