Билет №5. Представление информации в цифровых автоматах. Понятие кодирования. Алфавит. Позиционные системы счисления. Преобразование целых неотрицательных чисел из одной системы счисления в другую.

В процессе переработки информации цифровые ЭВМ - компьютеры, оперируют числами, которые представляются в некоторой системе счисления.  Система счисления - это совокупность приемов и правил для записи чисел цифровыми знаками. Запись числа в некоторой системе счисления часто называют кодом числа. Элементы (символы) алфавита, которые используются для записи чисел в некоторой системе счисления, принято называть цифрами. Каждой цифре данного числа однозначно сопоставляется ее количественный (числовой) эквивалент.

Алфавит — это множество (как правило конечное) символов или букв, например латинских букв и цифр. Примером распространённого алфавита является двоичный алфавит {0,1}. Конечная строка — это конечная последовательность букв алфавита. Например, двоичная строка — это строка из символов алфавита {0,1}. Также возможно построение бесконечных последовательностей из букв алфавита.

Позиционная система счисления (позиционная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда). Наиболее известной позиционной системой счисления является десятичная система счисления. Например, в десятичном числе 555 первая цифра справа означает 5 единиц, соседняя с ней - 5 десятков, а левая - 5 сотен.

Преобразование целых чисел

Для перевода необходимо исходное число разделить на основание новой системы счисления до получения целого остатка, который является младшим разрядом числа в новой системе счисления (единицы). Полученное частное снова делим на основание системы и так до тех пор, пока частное не станет меньше основания новой системы счисления. Все операции выполняются в исходной системе счисления.

Рассмотрим для примера перевод числа из десятичной системы счисления в двоичную систему счисления.

Возьмём десятичное число А10 = 124 и поделим его на основание двоичной системы, то есть число 2. Деление будем производить уголком:

В результате первого деления получим разряд единиц (самый младший разряд). В результате второго деления получим разряд двоек. Деление продолжаем, пока результат деления больше двух. В конце операции преобразования мы получили двоичное число 11111002.

Теперь то же самое число переведём в восьмеричную систему счисления. Для этого число 12410 разделим на число 8:

Как мы видим, остаток от первого деления равен 4. То есть младший разряд восьмеричного числа содержит цифру 4. Остаток от второго деления равен 7. то есть второй разряд восьмеричного числа – это цифра 7. Старший разряд получился равным 1. То есть в результате многократного деления мы получили восьмеричное число 1748.

Проверим, не ошиблись ли мы в процессе преобразования? Для этого преобразуем получившееся двоичное число в десятичную систему по обычной формуле разложения:

 1×82+7×81+4×80=6410+5610+410=124

;А можно ли осуществить перевод из восьмеричной системы счисления в двоичную делением? Можно! Но деление нужно произвести по правилам восьмеричной арифметики. Правила работы в восьмеричной системе счисления мы рассмотрим в следующей главе. Тем не менее, для полноты материала, рассмотрим пример перевода в двоичную форму полученного ранее восьмеричного числа 1748. Разделим его на основание новой системы счисления 2.

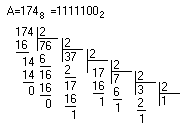
Как мы убедились выполнять деление в восьмеричной системе очень неудобно, ведь подсознательно мы делим в десятичной системе счисления. Давайте обратим внимание на то, что число 8 является степенью числа 2. То есть можно считать восьмеричную систему счисления просто более короткой записью двоичного числа. Это означает, что для представления восьмеричной цифры можно использовать три двоичных бита (8=23). Давайте составим таблицу соответствия. Она приведена в таблице 1.

Таблица 1. Таблица соответствия восьмеричных цифр и двоичного кода

Двоичный код	Восьмеричная цифра	Десятичный эквивалент
000	0	0
001	1	1
010	2	2
011	3	3
100	4	4
101	5	5
110	6	6
111	7	7

Используя эту таблицу можно просто заменить каждую восьмеричную цифру тремя двоичными битами. Три двоичных бита обычно называют триадой или трибитом. Теперь давайте переведём восьмеричное число 1748 в двоичную форму при помощи таблицы 7:

 

Аналогично можно выполнить перевод числа из двоичной системы в восьмеричную. Для этого двоичное число разбивают на триады относительно крайнего правого разряда (или двоичной запятой) и, используя таблицу 7, каждой триаде ставят в соответствие восьмеричную цифру.

Аналогичным образом можно выполнить перевод числа из шестнадцатеричной формы в двоичную и обратно. В этом случае для представления шестнадцатеричной цифры потребуется четыре двоичных разряда. Четыре двоичных разряда обычно называют тетрадой. Иногда при переводе иностранных книг используется термин нибл.

Давайте составим таблицу соответствия двоичных тетрад и шестнадцатеричных цифр. Для этого мы будем просто прибавлять единицу к значению предыдущей строки в каждом столбце таблицы, в соответствии с используемой в этом столбце системой счисления. Результат приведён в таблице 2.

В качестве примера использования таблицы 2 переведем шестнадцатеричное число 7С16 в двоичную форму представления:

Таблица 2. Таблица соответствия шестнадцатеричных цифр и двоичного кода

Двоичный код	Восьмеричная цифра	Десятичный эквивалент
0000	0	0
0001	1	1
0010	2	2
0011	3	3
0100	4	4
0101	5	5
0110	6	6
0111	7	7
1000	8	8
1001	9	9
1010	a	a
1011	b	b
1100	c	c
1101	d	d
1110	e	e
1111	f	f

Пример преобразования двоичного числа в восьмеричную и шестнадцатеричную форму приведён на рисунке 1.

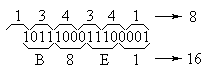
Рисунок 1. Пример преобразования двоичного числа в восьмеричную и шестнадцатеричную форму.

На этом рисунке внизу выделены двоичные тетрады и соответствующие им шестнадцатеричные цифры. Их соответствие можно проверить при помощи таблицы 2. Сверху выделены триады и соответствующие им восьмеричные цифры. Старшая триада получилась неполной. Её нужно дополнить старшими незначащими нулями для того, чтобы можно было бы воспользоваться таблицей 1.