Корреляционный анализ
Корреляционный анализ применяется для количественной оценки взаимосвязи двух наборов данных, представленных в безразмерном виде. Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине. Коэффициент корреляции, всегда обозначаемый латинской буквой r, используется для определения наличия взаимосвязи между двумя свойствами.
Связь между признаками (по шкале Чеддока) может быть сильной, средней и слабой. Тесноту связи определяют по величине коэффициента корреляции, который может принимать значения от -1 до +1 включительно. Критерии оценки тесноты связи показаны на рис.
Коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона r, который является безразмерным индексом в интервале от -1,0 до 1,0 включительно, отражает степень линейной зависимости между двумя множествами данных.
Пример: определить, существует ли взаимосвязь между следующими признаками:
Войдем в пункт меню «Сервис» и выберем команду «Анализ данных». В появившемся окне выберем раздел «Корреляция». После входа в него появиться следующее окно:
Аналогично предыдущему примеру вводим входной интервал ячеек с исходными данными. В нашем примере мы должны проверить взаимосвязь между жирностью молока и удоем коров. Поэтому мы выделяем интервал ячеек с этими данными. Так как у нас данные расположены в столбцах, то мы должны поставить флажок в разделе «группирование» по столбцам. Далее поставим флажок в разделе выходной интервал и укажем адрес ячейки E1 b и щелкнем по кнопке «ОК».
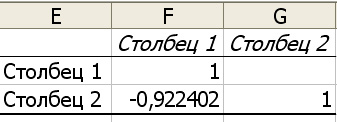
Полученный результат говорит о том, что между признаками существует очень высокая отрицательная корреляция, то есть при увеличении жирности молока удой наоборот, будет уменьшаться.
Применения пакета анализа и статистических функций в зоотехнической и ветеринарной работе.
Статистическая обработка данных применяется в племенной работе, обработке результатов исследований по внедрению новых рационов питания, условий содержания, использованию новых лекарственных препаратов и способах лечения животных.
В качестве примера возьмем применение нового рациона кормления животных. Как проверить, что новый рацион лучше старого? Как достоверно это можно доказать? Самый простой способ взять две группы животных с одинаковыми параметрами, одну группу кормить по старому рациону, вторую по-новому. Поместим на листе1 следующие данные.
Рассчитаем статистические показатели для каждой группы , используя «Описательную статистику» пакета анализа. Данные возьмем сразу по двум столбцам, а выходным интервалом поставим ячейку С1.
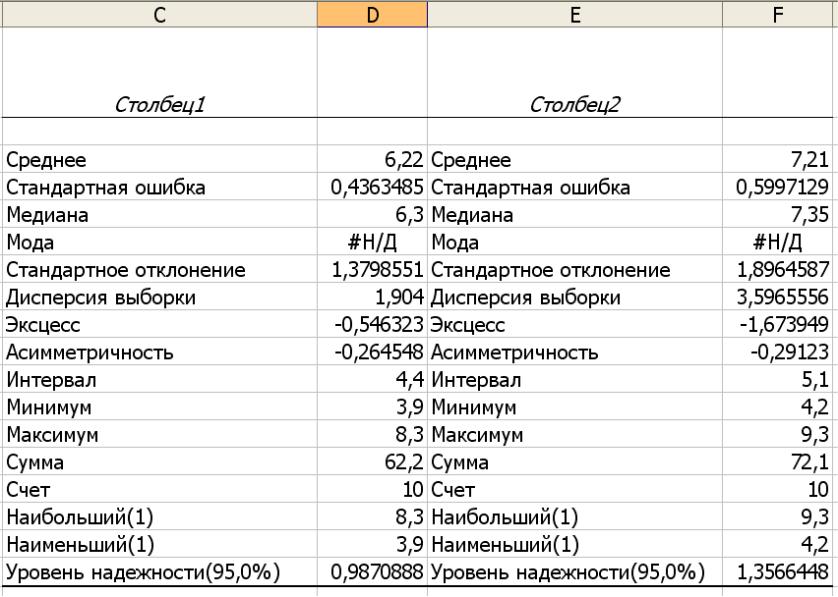
Получается, что во второй группе средний арифметический привес оказался больше. Как определить, достоверна эта разность в привесе между группами или нет? Для этого необходимо определить коэффициент достоверной разности по Стьюденту. Он определяется как частное от деления разности средних арифметических на корень квадратный из суммы квадратов ошибок этих средних арифметических.
В ячейке А 20 поместим пояснение «Коэффициент достоверной разности», затем для расчета самого показателя выделим ячейку В20 и внесем туда формулу
=(F3-D3)/КОРЕНЬ(F4^2+D4^2) ,
что даст нам результат 1,334
Рассчитаем число степеней свободы для наших двух выборок для этого. Число степеней свободы определяется суммой количества наблюдений с вычетом числа 2 (для нашего случая). В ячейке А 21 поместим пояснение «Число степеней свободы», затем для расчета самого показателя выделим ячейку В21 и внесем туда формулу
=D15+F15-2,
Что даст нам результат – 18.
Далее мы сравниваем значение критерия коэффициента достоверной разности, рассчитанного нами с соответствующим значением аналогичного коэффициента из таблицы Стьюдента с учетом рассчитанного числа степеней свободы. Минимальное значение коэффициента для числа степеней свободы 18 и вероятности 0,90 составляет 1,73 , что больше нашего значения. Это говорит о том, что разность между двумя средними показателями не достоверна. Таким образом, можно сделать вывод, что больший привес в группе животных, которых кормили по новому рациону обусловлена случайными причинами, а не новым рационом кормления.
f |
p |
|||||||
0.80 |
0.90 |
0.95 |
0.98 |
0.99 |
0.995 |
0.998 |
0.999 |
|
1 |
3.0770 |
6.3130 |
12.7060 |
31.8200 |
63.6560 |
127.6560 |
318.3060 |
636.6190 |
2 |
1.8850 |
2.9200 |
4.3020 |
6.9640 |
9.9240 |
14.0890 |
22.3270 |
31.5990 |
3 |
1.6377 |
2.35340 |
3.1820 |
4.5400 |
5.8400 |
7.4580 |
10.2140 |
12.9240 |
4 |
1.5332 |
2.13180 |
2.7760 |
3.7460 |
4.6040 |
5.5970 |
7.1730 |
8.6100 |
5 |
1.4759 |
2.01500 |
2.5700 |
3.6490 |
4.0321 |
4.7730 |
5.8930 |
6.8630 |
6 |
1.4390 |
1.9430 |
2.4460 |
3.1420 |
3.7070 |
4.3160 |
5.2070 |
5.9580 |
7 |
1.4149 |
1.8946 |
2.3646 |
2.9980 |
3.4995 |
4.2293 |
4.7850 |
5.4079 |
8 |
1.3968 |
1.8596 |
2.3060 |
2.8965 |
3.3554 |
3.8320 |
4.5008 |
5.0413 |
9 |
1.3830 |
1.8331 |
2.2622 |
2.8214 |
3.2498 |
3.6897 |
4.2968 |
4.7800 |
10 |
1.3720 |
1.8125 |
2.2281 |
2.7638 |
3.1693 |
3.5814 |
4.1437 |
4.5869 |
11 |
1.3630 |
1.7950 |
2.2010 |
2.7180 |
3.1050 |
3.4960 |
4.0240 |
4.4370 |
12 |
1.3562 |
1.7823 |
2.1788 |
2.6810 |
3.0845 |
3.4284 |
3.9290 |
4.1780 |
13 |
1.3502 |
1.7709 |
2.1604 |
2.6503 |
3.1123 |
3.3725 |
3.8520 |
4.2200 |
14 |
1.3450 |
1.7613 |
2.1448 |
2.6245 |
2.9760 |
3.3257 |
3.7870 |
4.1400 |
15 |
1.3406 |
1.7530 |
2.1314 |
2.6025 |
2.9467 |
3.2860 |
3.7320 |
4.0720 |
16 |
1.3360 |
1.7450 |
2.1190 |
2.5830 |
2.9200 |
3.2520 |
3.6860 |
4.0150 |
17 |
1.3334 |
1.7396 |
2.1098 |
2.5668 |
2.8982 |
3.2224 |
3.6458 |
3.9650 |
18 |
1.3304 |
1.7341 |
2.1009 |
2.5514 |
2.8784 |
3.1966 |
3.6105 |
3.9216 |
19 |
1.3277 |
1.7291 |
2.0930 |
2.5395 |
2.8609 |
3.1737 |
3.5794 |
3.8834 |
20 |
1.3253 |
1.7247 |
2.0860 |
2.5280 |
2.8453 |
3.1534 |
3.5518 |
3.8495 |
21 |
1.3230 |
1.7200 |
2.0790 |
2.5170 |
2.8310 |
3.1350 |
3.5270 |
3.8190 |
22 |
1.3212 |
1.7117 |
2.0739 |
2.5083 |
2.8188 |
3.1188 |
3.5050 |
3.7921 |
23 |
1.3195 |
1.7139 |
2.0687 |
2.4999 |
2.8073 |
3.1040 |
3.4850 |
3.7676 |
24 |
1.3178 |
1.7109 |
2.0639 |
2.4922 |
2.7969 |
3.0905 |
3.4668 |
3.7454 |
25 |
1.3163 |
1.7081 |
2.0595 |
2.4851 |
2.7874 |
3.0782 |
3.4502 |
3.7251 |
26 |
1.3150 |
1.7050 |
2.0590 |
2.4780 |
2.7780 |
3.0660 |
3.4360 |
3.7060 |
27 |
1.3137 |
1.7033 |
2.0518 |
2.4727 |
2.7707 |
3.0565 |
3.4210 |
3.6896 |
28 |
1.3125 |
1.7011 |
2.0484 |
2.4671 |
2.7633 |
3.0469 |
3.4082 |
3.6739 |
29 |
1.3114 |
1.6991 |
2.0452 |
2.4620 |
2.7564 |
3.0360 |
3.3962 |
3.8494 |
30 |
1.3104 |
1.6973 |
2.0423 |
2.4573 |
2.7500 |
3.0298 |
3.3852 |
3.6460 |
Задания для самостоятельной работы.
Определить, существует ли достоверная разность между скоростью выздоровления телят ( в сутках) в опытной и контрольной группах.
Опыт |
3 |
4 |
5 |
3 |
2 |
7 |
3 |
4 |
8 |
2 |
4 |
6 |
4 |
3 |
3 |
4 |
5 |
Контроль |
8 |
6 |
7 |
10 |
12 |
8 |
9 |
5 |
8 |
12 |
9 |
6 |
5 |
14 |
12 |
15 |
8 |