Занятие № 15 Тема: Введение в статистический анализ данных. Работа с пакетом «Анализ данных» программы Excel.

Методические указания: внимательно прочитать определения статистических показателей, вникнут в их сущность. Выполнить приведенные примеры расчетов в программе EXCEL. Выполнить задания для самостоятельной работы.

Поместим данные о среднесуточном удое выборочной группы из 48 коров в следующие ячейки листа 1 программы Excel.

Рассчитаем основные статистические показатели по этим данным.

Расчет средних показателей Расчет среднего арифметического.

Чтобы найти среднее арифметическое необходимо сложить все данные и разделить на число наблюдений. В нашем случае мы должны сложить данные по среднесуточному удою всех коров и разделить на их количество.

1 Способ основан на применении обычной расчетной формулы. Чтобы найти среднее арифметическое необходимо сложить все данные и разделить на число наблюдений. В нашем случае мы должны сложить данные по среднесуточному удою всех коров и разделить на их количество. Для этого в ячейку А 10 поместим следующую формулу:

=(СУММ(A2:F9))/48

Таким образом, мы применили функцию суммы для данных находящихся в ячейках интервала A2:F9 и разделили полученный результат на количество животных.

2 способ. В программе Excel собственно есть функция определения среднего арифметического. Для ее применения в ячейке А 11 поместите пояснение «Среднее арифметическое», затем для расчета самого показателя выделите ячейку В11, войдите в пункт меню «Вставка», и щелкните по пункту меню «Функция». В появившемся окне выберите категорию функции «статистические» и выберите функцию «срзнач»:

Появится окно , в раздел «Число1» которого нужно будет внести диапазон адресов ячеек с нашими данными. Это можно сделать путем простого выделения этих ячеек с помощью мыши.

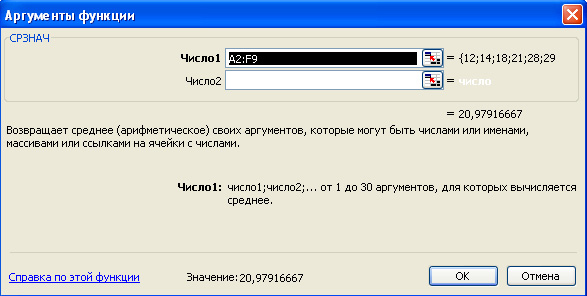
В итоге в ячейке А11 мы получим тот же результат, что и в ячейке А10.

Характеристики вариации данных и их расчет

Вариация (или еще ее по-другому называют изменчивость) показывает насколько показатели отличаются от средней арифметической в большую или меньшую сторону. Изменчивость признака очень важный показатель для ведения селекционной работы, чем выше изменчивость (вариабельность) признака, тем больше материала для искусственного отбора и тем более результативна селекционная работа.

Наиболее простыми характеристиками выборки являются максимум и минимум.

Минимум - наименьшее значение выборки.

Максимум - наибольшее значение выборки.

Размах - разница между наибольшим и наименьшим значениями выборки.

Дисперсия - среднее арифметическое квадратов отклонений значений от их среднего.

Стандартное отклонение - квадратный корень из дисперсии выборки - мера того, насколько широко разбросаны точки данных относительно их среднего.

Границы изменчивости признака лежат в пределах трех стандартных отклонений от средней арифметической в большую и меньшую сторону. Таким образом по этим 7 данным можно построить диаграмму, которая будет иметь при случайной выборке кривую нормального распределения.

Эксцесс показывает "остроту пика" распределения, характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение (пик заострен). Отрицательный эксцесс обозначает относительно сглаженное распределение (пик закруглен).

Если эксцесс существенно отличается от нуля, то распределение имеет или более закругленный пик, чем нормальное, или, напротив, имеет более острый пик (возможно, имеется несколько пиков). Эксцесс нормального распределения равен нулю.

Асимметрия или асимметричность показывает отклонение распределения от симметричного. Если асимметрия существенно отличается от нуля, то распределение несимметрично, нормальное распределение абсолютно симметрично. Если распределение имеет длинный правый хвост, асимметрия положительна; если длинный левый хвост - отрицательна.

Выбросы (outliers) - данные, резко отличающиеся от основного числа данных.

При обнаружении выбросов перед исследователем стоит дилемма: оставить наблюдения-выбросы либо от них отказаться. Второй вариант требует серьезной аргументации и описания. Полезным будет провести анализ данных с выбросами и без и сравнить результаты.

Следует помнить, что при применении классических методов статистического анализа, которые, как правило, не являются робастными (устойчивыми), наличие выбросов в наборе данных приводит к некорректным результатам. Если набор данных относительно мал, исключение данных, которые считаются выбросами, может заметно повлиять на результаты анализа.

Наличие выбросов в наборе данных может быть связано с появлением так называемых "сдвинутых" значений, связанных с систематической ошибкой, ошибок ввода, ошибок сбора данных и т.д. Иногда к выбросам могут относиться наименьшие и наибольшие значения набора данных.