2.2 Основна система методу переміщень

Розрахунок статично невизначуваної рами полягає в тому, що замість неї розглядається така створена з неї система (рис. 2.4), розрахунок якої можна здійснити за допомогою вже відомих засобів. Така нова система називається основною системою, вона дає можливість усунути переміщення всіх вузлів системи.

Рисунок 2.2 – Картина геометричної незмінності (перекосів) рами

Основну систему отримують із заданої шляхом накладання на всі вузли рами додаткових в’язей двох видів, які перешкоджають повороту жорстких вузлів та їх можливим лінійним переміщенням, за рахунок чого рама перетворюється в систему однопрогонових балок постійної жорсткості з нерухомими опорами, для розрахунку котрих є готові таблиці (додаток Б).

Число в’язей, що вводяться в основну систему, дорівнює ступеню кінематичної невизначуваності системи, тобто трьом. Число додаткових «плаваючих» затиснень співпадає зі ступенем кутових переміщень , а число додаткових стержнів – зі ступенем можливих лінійних переміщень вузлів .

Таким чином, основна система (рис. 2.4) перетворює вихідну розрахункову схему статично невизначеної рами в набір однопрогонових балок постійної жорсткості з нерухомими опорами, які не дають змоги кінцям балок мати кутові та поступальні переміщення.

2.3 Еквівалентна система

Вузли вихідної схеми рами (рис. 2.3) при зовнішньому навантаженні мають переміщення – кути повороту жорстких вузлів В і С та їх поступальні переміщення в горизонтальному напрямку. У створеній основній системі (рис. 2.4) ці переміщення вузлів виключені накладеними додатковими в’язями – «плаваючими» затисненнями та додатковим горизонтальним опорним стержнем.

Для усунення цих відмін у деформаціях вихідної та основної систем надамо в основній системі додатковим в’язям поки що невідомі переміщення цих вузлів (рис. 2.5), тобто, жорсткий вузол В, разом з «плаваючим» затисненням (1), повернемо на кут, що дорівнює , другий жорсткий вузол С, разом із рухомим затисненням (2), повернемо на кут , і надамо цим вузлам, разом з опорним вузлом Е і додатковим стержнем (3), переміщення в горизонтальному напрямі, на величину, що дорівнює , а також розмістимо задане зовнішнє навантаження (рис. 2.5).

Таким чином, за невідомі приймаємо кути повороту жорстких вузлів рами та поступальне переміщення вузлів рами в горизонтальному напрямку.

Якщо ці переміщення вузлів () будуть дорівнювати дійсним кутовим переміщенням рами від дії зовнішнього навантаження, тоді створена основна система, разом із переміщенням вузлів () і зовнішнім навантаженням (рис. 2.5), за умовами роботи системи, буде еквівалентна вихідній системі (рис. 2.3).

2.4 Канонічні рівняння

У додаткових в’язях основної системи від навантаження виникають реактивні сили, яких немає у вихідній рамі, через відсутність цих додаткових в’язей. У «плаваючих» затисненнях жорстких вузлів виникають реактивні моменти, у додаткових опорних стержнях – реактивні сили, тобто реакції.

Отже, необхідно скласти математичні умови реактивних сил накладених додаткових в’язей, які дорівнюють нулю.

На підставі принципу суперпозиції сумарний реактивний момент у «плаваючому» затисненні першого вузла В від невідомих переміщень () і зовнішнього навантаження прирівняємо до нуля. Реактивний момент у «плаваючому» затисненні другого вузла С від невідомих переміщень () і зовнішнього навантаження прирівняємо до нуля. Сумарну реакцію в додатковому опорному стержні (третій додатковій в’язі) від невідомих переміщень () і зовнішнього навантаження прирівняємо до нуля.

Канонічні рівняння методу переміщень встановлюють еквівалентність основної та заданої систем. Для заданої рами вони мають наступний вигляд:

Рисунок 2.3 – Розрахункова схема рами

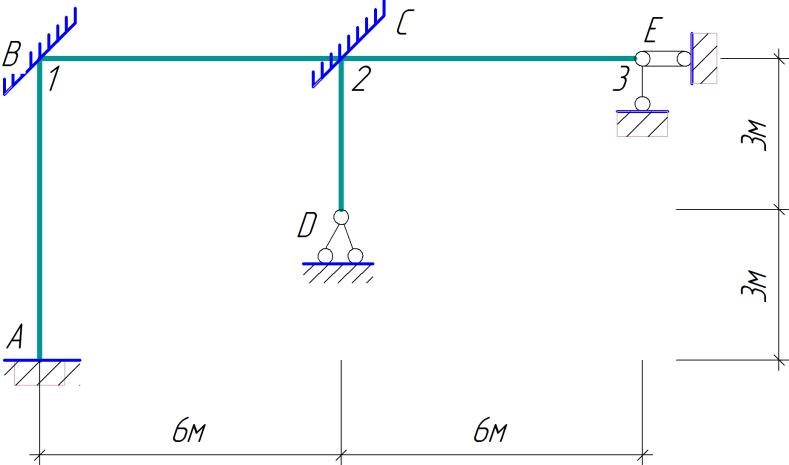
Рисунок 2.4 – Основна система

Рисунок 2.5 – Еквівалентна система

(2.2)

Таким чином, фізичний зміст кожного з цих рівнянь полягає в тому, що сумарна реактивна сила у відповідній додатковій в’язі (реактивний момент у «плаваючому» затисненні, або реакція в додатковому опорному стержні) основної системи від усіх невідомих переміщень і зовнішнього навантаження дорівнює нулю.

Ця сукупність залежностей є розв’язувальними рівняннями та називається системою канонічних рівнянь методу переміщень (2.2). Ці рівняння є рівняннями статичної рівноваги системи.

Основними невідомими цих рівнянь являються переміщення, виключені додатковими в’язями, де і – кути повороту жорстких вузлів В і С, та – незалежне поступальне переміщення цих вузлів у горизонтальному напрямі.

Коефіцієнти при невідомих першого рядка системи канонічних рівнянь являють собою одиничний реактивний момент у «плаваючому» за-тисненні вузла В основної системи від дії одиничних невідомих переміщень .

Коефіцієнти при невідомих другого рядка канонічних рівнянь являють собою одиничний реактивний момент у «плаваючому» затисненні вузла С основної системи від дії одиничних невідомих переміщень .

Коефіцієнти при невідомих третього рядка канонічних рівнянь являють собою одиничну реакцію в додатковому опорному стержні основної системи від дії невідомих переміщень .

Вільні члени канонічних рівнянь являють собою вантажні реакції в додаткових в’язях основної системи від дії зовнішнього навантаження.

Для визначення одиничних реакцій та вільних членів канонічних рівнянь необхідно мати епюри внутрішніх зусиль в основній системі методу переміщень в одиничних та вантажному станах.