1.9 Перевірка епюр дійсних внутрішніх зусиль м, q, n (статична й кінематична)

Для перевірки правильності розрахунку будь-якої статично невизначуваної системи необхідно виконати її перевірку – статичну й кінематичну.

Статична перевірка полягає в розгляді рівноваги вузлів системи. З цією метою необхідно вирізати кожний вузол та прикласти до нього моменти в перерізах прикріплених до вузла стержнів і зосереджені моменти від зовнішнього навантаження. Величини та напрямки моментів , що перевіряються. Рівняння рівноваги вузлів у вигляді суми моментів відносно нього повинні задовольнятися:

.

Кінематична перевірка полягає у визначенні переміщення, яке завідомо дорівнює нулю, тобто переміщення в напрямку існуючих в’язей. Для обчислення такого переміщення в заданій статично невизначуваній системі необхідно відкинути зайві в’язі, перетворивши її у статично визначувану, тобто в основну систему методу сил.

Далі до цієї основної системи слід прикласти узагальнені одиничні сили у напрямку відкинутої в’язі «і».

2 Приклад розрахунку статично невизначуваної рами за методом переміщень у канонічній формі

Схему рами та навантаження наведено на рис. 2.1.

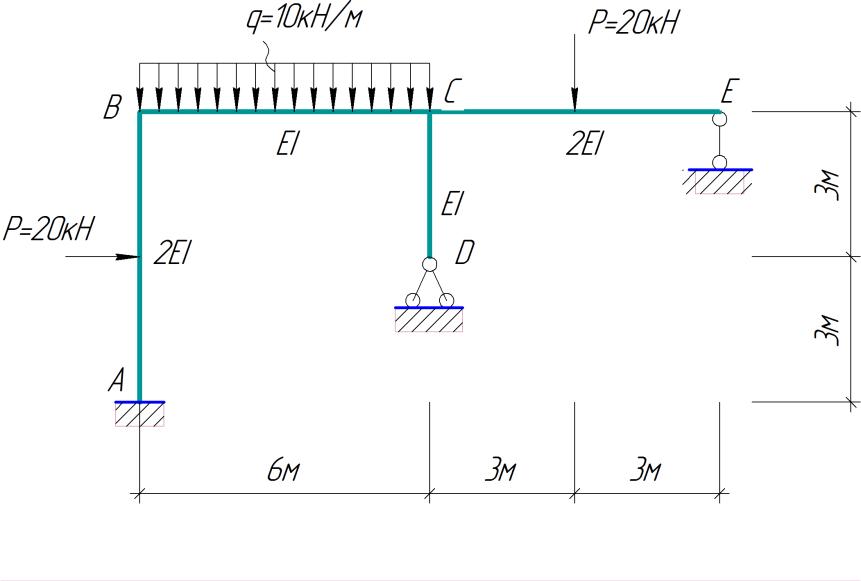
Рисунок 2.1 – Розрахункова схема

Для заданої рами потрібно:

1. Визначити ступінь кінематичної невизначуваності рами.

2. Створити основну та еквівалентну системи методу переміщень.

3. Скласти систему канонічних рівнянь для визначення основних невідомих переміщень.

4. Побудувати в основній системі епюри згинальних моментів в одиничних і вантажному станах.

5. Визначити коефіцієнти та вільні члени системи канонічних рівнянь статичним способом. Виконати їх перевірки.

6. Розв’язати систему канонічних рівнянь.

7. Побудувати парціальні епюри згинальних моментів.

8. Побудувати остаточну епюру дійсних згинальних моментів рами.

9. Виконати статичну та кінематичну перевірку остаточної епюри зги-нальних моментів.

10. Побудувати епюри поперечних та поздовжніх сил.

11. Визначити опорні реакції й виконати загальну перевірку умов рівноваги заданої рами.

12. Побудувати деформовану вісь рами.

2.1 Ступінь кінематичної невизначуваності рами

Ступінь кінематичної невизначуваності рами обчислюється за формулою:

, (2.1)

де − кількість кутових переміщень жорстких вузлів. Рама має два жорсткі вузли – вузол В і вузол С.

.

− кількість незалежних поступальних переміщень вузлів рами, що дорівнює геометричній змінності системи , яка утворюється із заданої шляхом введення в усі жорсткі вузли (включно з опорними) наскрізних (повних) шарнірів (рис. 2.2):

;

,

де – кількість простих дисків (стержнів);

– кількість простих шарнірів;

– кількість опорних простих в’язей;

– кількість вузлів в’язей;

– кількість стержнів рами.

;

.

Отже, для перетворення шарнірної системи в геометрично незмінювану систему достатньо закріпити вузли і від горизонтального переміщення введенням додаткового горизонтального опорного стержня. Таким чином, рама має одне незалежне поступальне переміщення вузлів.

Ступінь кінематичної невизначуваності заданої рами

.