1.5 Епюри зусиль в основній системі методу переміщень
Основна система методу переміщень являє собою набір однопрогонових балок, що зображені на рис. 1.7. Для цих елементів основної системи можна заздалегідь визначити опорні реакції й побудувати епюри згинальних моментів і поперечних сил від будь-якого навантаження та переміщення.
а) статично визначувана балка; б) і в) статично невизначувані балки
Рисунок 1.7 – Види балок
Балка на рис. 1.7 (а) статично визначувана, отже, епюри внутрішніх зусиль від навантажень будуються як в простих балках.
Для побудови епюр внутрішніх зусиль у елементах, що становлять статично невизначувані балки на рис. 1.7 (б, в), результати розрахунків при різних граничних умовах від одиночних значень кутів повороту жорстких опор балок, одиничних поступальних переміщень їх опор і від зовнішнього навантаження наведено в додатку Б.
Одиничні
та вантажні епюри для основної системи
методу переміщень являють собою
сукупність епюр в окремих балках, що
складають основну систему, від переміщень
їхніх опор або від дії місцевого
навантаження. Побудова цих епюр від
одиничних значень невідомих кутів
повороту та поступального переміщення
вузлів, тобто опор балок та зовнішнього
навантаження, зображена на рис. 1.8, де
побудовані в основній системі (1.8,
б)
методу переміщень одиночні
(рис. 1.8, в, г, д) та вантажна
(рис. 1.8, е) епюри згинальних моментів.
На рисунку 1.9 побудовані одиничні епюри
(рис. 1.9 в, г, д) та вантажна епюра (рис.
1.9, е).
Після побудови одиничних та вантажних епюр згинальних моментів у основній системі методу переміщень можна визначити коефіцієнти та вільні члени канонічних рівнянь способом перемноження епюр на підставі формули Мора або статичним способом.
1.6 Статичний спосіб визначення коефіцієнтів і вільних членів системи канонічних рівнянь та їх перевірка
Коефіцієнти
й вільні члени системи канонічних
рівнянь методу переміщень визначаються,
виходячи з їхнього фізичного запису,
тобто вони являють собою реакції, що
виникають у відповідній додатковій
в’язі основної системи від одиничного
значення невідомого переміщення або
зовнішнього навантаження. Додатні
напрями реакцій збігаються з напрямами
відповідних невідомих переміщень
.
Зазначені реакції поділяються на два
види.
а)
основна система; б) еквівалентна система;
в) епюра
;
г) епюра
;
д) епюра
;
е) епюра
Рисунок 1.8 – Рама 1 та епюри згинальних моментів
а) основна система; б) еквівалентна система; в) епюра ; г) епюра ; д) епюра ; е) епюра
Рисунок 1.9 – Рама 2 та епюри згинальних моментів
1. Реактивні моменти у введених рухомих затисненнях жорстких вузлів;
2. Реакції у введених додаткових опорних стержнях.
Коефіцієнти та вільні члени системи канонічних рівнянь визначаються способом перемноження епюр (формула Мора), або статичним способом.
1.6.1 Реактивні моменти у введених рухомих затисненнях
Для
визначення реактивних моментів статичним
способом необхідно виокремити вузол з
епюри згинальних моментів відповідного
одиничного або вантажного стану із
введеним рухомим затисненням. До цього
вузла прикладається невідомий реактивний
момент у затисненні, напрямок якого
співпадає з напрямком відповідного
переміщення, а також згинальні моменти
в перерізах стержнів відповідної епюри
згинальних моментів. Складається
рівняння рівноваги цього виокремленого
вузла та визначаємо реактивний момент
(
).
Так
для рами на рис. 1.8 (а) коефіцієнт
– це
реактивний момент у рухомому затисненні
вузла 1 основної системи (рис. 1.4, б) від
одиничного кута повороту
в першому одиничному стані (рис. 1.8, в).
Складаємо рівняння рівноваги цього
виокремленого вузла 1 (рис. 1.10, а):
;
;
.
Коефіцієнт
–
це реактивний момент у рухомому затисненні
вузла 1 основної системи (рис 1.10, б)
від одиничного кута повороту
,
тобто в другому одиничному стані (рис.
1.8, г). Виокремлюємо вузол 1 з епюри
і складаємо рівняння його рівноваги
(рис. 1.10, б):
;
.
Коефіцієнт
–
це реактивний момент у рухомому
затисненні, вузла 1 основної системи
(рис. 1.4, б), від одиничного поступального
переміщення
,
тобто в третьому одиничному стані (рис.
1.8, д). Виокремлюємо вузол 1 з епюри
і
складаємо рівняння його рівноваги
(рис. 1.10, в):
;
.
Вільний
член
−
це реактивний момент у рухомому затисненні
вузла 1 основної системи (рис. 1.4, б), від
зовнішнього навантаження,
тобто
у вантажному стані (рис. 1.8, е). Виокремлюємо
вузол 1 з епюри
і
складаємо рівняння його рівноваги (рис.
1.10, г):
;
.
На
рис. 1.11 (а, б, в, г) наведено вузол 2,
рівновагу якого слід розглянути для
визначення коефіцієнтів і вільного
члена другого рядка системи канонічних
рівнянь, що являють собою реактивні
моменти в рухомому затисненні, вузла 2
основної системи (рис. 1.4, б ), від одиничних
невідомих переміщень
(рис. 1.8, в, г, д) і зовнішнього навантаження
(рис 1.8, е).
а)
визначення
;
б) визначення
;
в)
визначення
;
г)
визначення
Рисунок 1.10 – Визначення одиничних коефіцієнтів та вільних членів
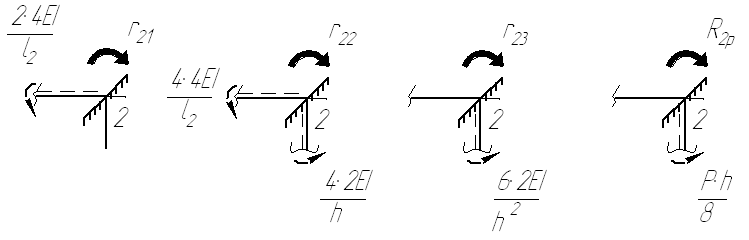
а)
визначення
;
б) визначення
;
в)
визначення
;
г)
визначення
Рисунок 1.11 – Визначення одиничних коефіцієнтів та вільних членів