2.9 Перевірка епюр дійсних внутрішніх зусиль м, q, n(статична й кінематична)

Кінематична (деформаційна) перевірка епюри згинальних моментів .

Суть цієї перевірки полягає в тому, що переміщення в напрямку будь-якої відкинутої в’язі повинно дорівнювати нулю.

Для виконання цієї перевірки приймаємо основну геометрично незмінну й статично визначену систему (рис 2.19), яку одержуємо із вихідної системи, відкидаючи зайві в’язі, і прикладаємо до неї реакції відкинутих в’язей вузлів D і E, надаючи їм одиничних значень . Ці одиничні реакції відкинутих в’язей вибираємо таким чином, щоб сумарна одинична епюра згинальних моментів (рис. 2.19) від їхньої дії заповнювала всі стержні рами.

Визначаємо кількість зайвих в’язей вихідної рами за формулою Чебишова (рис. 2.20):

.

Деформаційну перевірку виконуємо шляхом перемноження остаточної епюри згинальних моментів () на сумарну одиничну епюру згинальних моментів (), побудовану в статично визначеній системі.

Рисунок 2.19 – Статично визначена система

Рисунок 2.20 – Сумарна одинична епюра моментів в статично визначеній системі

Обчислюємо сумарне переміщення в напрямку трьох відкинутих в’язей:

Похибка: %

Статична перевірка рівноваги рами.

Для виконання статичної перевірки епюри розглядаємо умови рівноваги вузлів В і С рами (рис 2.21).

Вузол В Вузол С

Рисунок 2.21 – Умова рівноваги вузлів рами

Для виконання перевірки рівноваги всієї рами (рис. 2.22) прикладаємо до рами зовнішнє навантаження й визначені опорні реакції (рис. 2.23).

Перевіряємо, чи задовольняються умови рівняння рівноваги:

;

Рисунок 2.22 – Розрахункова схема

Визначаємо опорні реакції з умови рівноваги опорних вузлів рами через зусилля в перерізах, що одержані з епюр , Q, N.

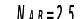
Рисунок 2.23 – Опорні реакції заданої рами

2.10 Обчислення переміщень в статично невизначених системах

Під впливом зовнішніх навантажень рама деформується, тобто координати, що характеризують положення кожного перерізу, змінюються – переміщуються. Обчислення переміщень необхідно для розрахунку споруди на жорсткість. За допомогою формули Максвела – Мора маємо можливість обчислити будь-яке переміщення в будь-якій стержневій системі через внутрішні зусилля двох її станів. Для заданої системи (рис. 2.19) перший стан – вантажний, тобто це побудована епюра згинальних моментів для заданої рами (рис. 2.15, а), другий стан – допоміжний, зумовлений дією одиничної узагальненої сили, яка відповідає переміщенню (лінійному, або кутовому), що розшукується. Для створення одиничного допоміжного стану (стан « і ») приймаємо статично визначену систему без зовнішнього навантаження й прикладаємо в напрямку шуканого переміщення одиничну узагальнену силу , або , що відповідає напрямку переміщення перерізу в точці « і ».

Наприклад, для визначення лінійного переміщення перерізу в точці « і » в горизонтальному напрямку прикладаємо одиничну узагальнену силу по цьому напрямку й будуємо допоміжну одиничну епюру згинальних моментів і визначаємо переміщення перерізу за формулою Мора:

.

Для заданої рами, в результаті розв’язання системи канонічних рівнянь, визначені кути повороту вузлів В і С () та їх лінійне переміщення в горизонтальному напрямку ().

Для побудови деформованої вісі заданої рами (рис. 2.23) визначаємо додаткові лінійні переміщення перерізів, взятих в середині кожного стержня рами (рис. 2.24).

Рисунок 2.24 – Схема розміщення перерізів для визначення їх переміщень

а) одинична епюра ; б) одинична епюра ; в) одинична

епюра ; г) одинична епюра

Рисунок 2.25 – Одиничні епюри згинальних моментів допоміжних

станів в основній системі методу сил

Визначаємо переміщення перерізу в точці «а». Будуємо одиничну епюру згинальних моментів в основній системі методу сил (рис. 2.25, а).

Визначаємо переміщення :

.

Визначаємо переміщення перерізу рами в точці «b». Будуємо одиничну епюру згинальних моментів в основній системі методу сил (рис. 2.25, б).

Визначаємо переміщення :

Визначаємо згинальні моменти в перерізах і на епюрі за формулою:

.

Рисунок 2.26 – Визначення та

;

.

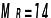
Рисунок 2.27 – Визначення і

Визначаємо переміщення перерізу рами в точці «c». Будуємо одиничну епюру згинальних моментів в основній системі методу сил (рис. 2.25, в).

Визначаємо переміщення :

Визначаємо переміщення перерізу рами в точці «d». Будуємо одиничну епюру згинальних моментів в основній системі методу сил (рис. 2.25, г).

Визначаємо переміщення :

Будуємо деформовану вісь рами (рис. 2.28).

Рисунок 2.28 – Деформована вісь рами

СПИСОК РЕКОМЕНДОВАНИХ ЛІТЕРАТУРНИХ ДЖЕРЕЛ

Основна література:

1. Баженов В. А. Будівельна механіка. Комп'ютерні технології / В. А. Баженов, А. В. Перельмутер, О. В. Шишов; за заг. ред. д. т. н., проф. В. А. Баженова. – К.: Каравела, 2009. – 694 с.

2. Дарков А.В. Строительная механика / А. В. Дарков, Н. Н. Шапошников. – 8 изд. перераб. и доп. – М:. 1986. – 608 с.

3. Строительная механика. под ред. Ю.И.Бутенко. – К: Высш. шк., 1989. – 479 с.

4. Строительная механика. Руководство к практическим занятиям / под ред. Ю. И. Бутенко. – 2-е изд. перераб. и доп. – К.: Высш. шк., 1989. – 367 с.

5. Киселев В. А. Строительная механика / В. А. Киселев. – 3е изд., доп. – М.: Стройиздат, 1986. – 512 с.

6. Зенкевич О. Метод конечных элементов в теории сооружений и в механике сплошных сред / О. Зенкевич, И. Чанг. – М.: Мир, 1974. – 239 с.

Додаткова література:

1. Методичні вказівки до виконання РГР з дисципліни «Будівельна механіка» «Розрахунок багатопрогінної статично визначеної балки» (для студентів за спеціальністю 7.092109 «Автомобільні дороги і аеродроми») / укл.: М. М. Чальцев, Л. П. Коновалова, І. О. Кисіль, А. О. Плашенко. – Горлівка: АДІ ДонНТУ, 2003. – 62 с.

2. Методичні вказівки до виконання РГР з дисципліни «Будівельна механіка» «Розрахунок тришарнірної арки» (для студентів спеціальності 7.092105 «Автомобільні дороги та аеродроми)/ укл.: М. М. Чальцев, Л. П. Коновалова, А. О. Плашенко. – Горлівка: АДІ ДонНТУ, 2003. – 37 с.

3. Методичні вказівки до виконання РГР з дисципліни «Будівельна механіка» «Розрахунок нерозрізної балки» (для студентів спеціальності 7.092105 «Автомобільні дороги і аеродроми)/ укл.: М. М. Чальцев, Л. П. Коновалова, А. О. Плашенко. – Горлівка: АДІ ДонНТУ, 2004. – 47 с.

4. Методичні вказівки до виконання РГР з дисципліни «Будівельна механіка» «Розрахунок плоскої статично невизначеної рами методом сил» (для студентів спеціальності 7.092105 «Автомобільні дороги і аеродроми»/ укл.: М. М. Чальцев, Л. П. Коновалова, С. Ю. Рижков, А. О. Плашенко. –Горлівка: АДІ ДонНТУ, 2003. – 51 с.

ДОДАТОК А

Таблиця А.1 – Вихідні дані варіантів розрахунково-графічних робіт

В	Б	А	В	Б	В	А	Б	В	А	Б	В	А	Б
№ схеми	розміри в метрах			вантаж						жорсткість
				, кН	, кН	, кН	, кН/м	, кН/м	, кН/м
1	4	7	5	16	8	10	6	2	3	1	5	2	3
2	5	9	6	18	10	12	7	3	4	2	4	3	1
3	6	10	7	20	14	18	9	4	5	3	2	1	4
4	7	4	8	12	16	20	5	8	6	4	3	2	1
5	8	6	9	14	12	10	3	5	7	5	1	3	2
6	4	5	6	21	18	14	10	7	8	1	2	4	3
7	6	9	10	24	8	12	4	5	2	2	3	1	4
8	7	6	5	10	20	18	3	2	4	3	4	2	5
9	10	7	8	22	14	16	4	3	5	4	5	3	2
10	9	5	7	16	21	8	5	6	3	5	1	2	3

Наприклад :

Шифр	–	08	–	049
Букви	–	А	–	БВ

Із кожного вертикального стовпця таблиці А.1, позначеного наверху певною буквою, потрібно взяти тільки одне число, номер рядка якого збігається з номером букви (дані для цього прикладу підкреслені в таблиці).

Розрахункова схема

Рисунок А.1 – Схеми статично невизначуваних рам

Рисунок А.2 – Схеми статично невизначуваних рам

ДОДАТОК Б

Одиничні та вантажні епюри моментів та реакції опор балок основної системи методу переміщень

ЕЛЕКТРОННЕ НАВЧАЛЬНО-МЕТОДИЧНЕ ВИДАННЯ

Чальцев Михайло Миколайович

Коновалова Людмила Павлівна

МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ РОЗРАХУНКОВО-ГРАФІЧНОЇ РОБОТИ «РОЗРАХУНОК ПЛОСКОЇ СТАТИЧНО НЕВИЗНАЧУВАНОЇ РАМИ МЕТОДОМ ПЕРЕМІЩЕНЬ» З ДИСЦИПЛІНИ «БУДІВЕЛЬНА МЕХАНІКА» (ДЛЯ СТУДЕНТІВ НАПРЯМУ ПІДГОТОВКИ 6.060101 «БУДІВНИЦТВО»)

Підписано до випуску . .20 р. Гарнітура Times New.

Умов. друк. арк. . Зам. № .

Державний вищий навчальний заклад

«Донецький національний технічний університет»

Автомобільно-дорожній інститут